알고리즘 문제풀이
1.완전탐색 - 피로도 (Level 2)

풀이: dungeons 리스트에 대해 모든 가능한 순서로 나열한 경우를 순열(Permutations)로 생성하고,생성한 순열 리스트를 모두 탐색하며 탐색 가능한 최대 던전 수를 찾아 리턴한다.
2.완전탐색 - 카펫 (Level 2)

3.완전탐색 - 전력망을 둘로 나누기 (Level 2)

wires 리스트에서 차례대로 전체 전선 중 하나씩 끊는 모든 경우를 고려한다.전선 하나를 끊어서 쪼개진 두 트리의 크기를 구하여 절댓값 차이를 계산한다.해당 절댓값 차이가 지금까지의 최소 절댓값 차이(min_diff)보다 작다면 갱신한다.최종 최소 절댓값 차이를 리턴
4.완전탐색 - 모음사전 (Level 2)

풀이: 알파벳 모음만을 조합해서 단어를 만들고, 최소 길이 1부터 5까지이므로 해당 알파벳들을 사용하여 중복순열(순서가 상관있으므로)을 1부터 5까지의 길이로 생성하여 dict 리스트에 가능한 단어를 모두 추가한 후, sort()하여 사전순으로 정렬한 후에 dict.i
5.완전탐색 - 소수 찾기 (Level 2)

6.DFS/BFS - 타겟 넘버 (Level 2)

7.LIS(Longest Increasing Subsequence, 최장 증가 부분 수열) - 징검다리 문제
풀이: LIS의 길이만 필요하기 때문에 더 작은 수로 이어지는 LIS 후보를 만들어 앞으로 올 수 있는 수들의 여지를 넓힌다.최종 lis 배열의 길이가 lis의 길이가 된다.
8.DFS/BFS - 네트워크 (Level 3)

9.DFS/BFS - 게임 맵 최단거리 (Level 2)

업로드중..업로드중..2차원 배열 상에서 최단거리 구하기 -> queue를 활용한 BFS
10.DFS/BFS - 단어 변환 (Level 3)

words 리스트 내의 각 단어까지 가는 데 걸린 거리(단계)를 누적해서 저장할 words_dist 리스트를 추가로 생성하여 BFS로 구현
11.정렬 - 가장 큰 수 (Level 2)

functools 라이브러리의 cmp_to_key 를 사용하여 커스텀 정렬함수 만들어서 정렬하기정렬 기준: A+B vs B+A 형식으로 비교ex) 100 + 10 = "10010"10 + 100 = "10100"에서 "10100" > "10010" \-> 단순 자리수
12.정렬 - H-Index (Level 2)

13.DP - 퇴사

14.구현 - 주사위 굴리기

주사위를 동, 서, 남, 북으로 굴릴 때 각 위치의 숫자들이 어디로 이동하는지를 잘 구현해야 함
15.구현 - 로봇 청소기

16.완전탐색 - 연구소

itertools 안쓰고 조합 구하는 방법으로 다시 풀어보기중요 포인트: 빈 공간(0)의 좌표를 모두 저장해서 3개씩 조합할 수 있는 가능한 모든 조합을 탐색해야 함
17.구현 - 경사로

중요 포인트: 1) 경사로를 만들 때, maps의 값을 직접 수정하지 않고 visited 리스트를 새로 생성하여 경사로 설치 유무를 따로 저장하기2) 가로 길 확인 후 세로 길 확인 시 가로 길에 설치한 경사로가 영향을 주면 안됨 (visited 배열 두개 사용해서 해
18.구현 - 톱니바퀴

입력 인덱스 범위와 코드 내 인덱스 범위 틀리는 것 주의왼쪽 오른쪽 신경쓰다가 자기 자신 회전 잊지 않기함수 호출할 때 인자 정확히 넘겨주기
19.구현, 완전탐색 - 14500번: 테트로미노

20.구현, DFS - 19236번: 청소년 상어

중요 포인트:1) DFS 호출 전 maps, d_list, fish_pos 전부 deepcopy해서 상어 이동시키고 dfs호출하기 (모든 경우를 실험해봐야 하므로 현재 상태를 복사해놔야 함)2) 함수 호출 시 전역 변수 참조하지 않도록 인자 잘 넘기기 (현재 상태에 따
21.구현, BFS - 민트 초코 우유

22.구현, BFS - 16234번: 인구 이동

23.BFS - 17471번: 게리맨더링

업로드중..
24.구현, 브루트포스 - 15686번: 치킨 배달

25.구현, BFS - 20058번: 마법사 상어와 파이어스톰

26.BFS - 19238번: 스타트 택시

27.DFS - 13460번: 구슬 탈출 2

28.시뮬레이션 - 미생물 연구

29.구현 - 1283번: 단축키 지정

30.DP - 15989번: 1, 2, 3 더하기 4

DFS로 풀면 작은 n에서는 잘 되지만, n이 커지면 경우의 수가 너무 많아 시간초과가 발생\-> DP로 풀어야 함!
31.시뮬레이션 - 20055번: 컨베이어 벨트 위의 로봇

각 칸의 내구도를 저장하는 A_list와 로봇의 유무를 저장하는 robot_list 구현 시 리스트 대신 deque로 구현하면 .rotate(1)을 사용하여 오른쪽으로 1칸 회전을 쉽게 할 수 있음.rotate(-1)은 왼쪽으로 1칸 회전n, k = map(int, i
32.DFS - 12919번: A와 B 2

S -> T로 정방향 탐색(시간초과)보다 T -> S로 역방향 탐색하는 것이 경우의 수가 훨씬 적어 효율적이기 때문에 시간초과가 나지 않음!
33.문자열 - 20437번: 문자열 게임 2

3번: 어떤 문자를 k개 포함하는 가장 짧은 연속 문자열의 길이 구하기 (결국 시작과 끝이 어떤 문자여야 가장 짧아짐)4번: 어떤 문자를 k개 포함하면서 시작과 끝이 해당 문자인 가장 긴 연속 문자열의 길이 구하기\-> 3번과 4번은 각각 따로
34.구현 - 14719번: 빗물

맵의 왼쪽 끝과 오른쪽 끝에서 벽이 아닌 곳에서부터 출발해서 벽에 닿을 때까지의 공간에는 빗물이 찰 수 없기 때문에 해당 부분을 bfs로 탐색하여 맵에 표시한 후, 해당 공기 부분과 벽 부분이 제외된 맵에서 0의 갯수(=빗물 총량)만 카운트했다.
35.그래프 탐색 - 2668번: 숫자고르기

1) 아래 숫자들의 set으로부터 가능한 모든 부분집합을 생성하여 해당 집합의 아래 숫자 리스트를 구해서 정렬 후 비교 시조합 + 정렬 + 비교를 반복하므로 최악의 시간복잡도는 O(2^n \* nlogn) 이상이므로 시간초과 발생함2) 문제 구조가 그래프의 연결 구조(
36.투포인터, 브루트포스 - 2531번: 회전초밥

그냥 완전탐색 시 이중 for문으로 O(nk)가 되어 시간초과 발생함.\-> 슬라이딩 윈도우 기법을 사용하면 O(n)만에 가능!다음 구간은 이전 구간에서 1개 빠지고 1개 들어오는 형태로 구현, defaultdict로 종류별 초밥 개수 관리하고, 총 초밥 종류 개수는
37.그리디 - 17615번: 볼 모으기

1) 레드를 모두 왼쪽으로 옮기기2) 레드를 모두 오른쪽으로 옮기기3) 블루를 모두 왼쪽으로 옮기기4) 블루를 모두 오른쪽으로 옮기기또한, 각 경우의 이동 횟수는 (현재 컬러의 전체 갯수) - (현재 컬러의 현재 방향의 끝에 존재하는 현재 컬러 덩어리 갯수) 로 계산할
38.DP - 1446번: 지름길

39.구현, 브루트포스 - 15683번: 감시

40.브루트포스 - 14888번: 연산자 끼워넣기

41.구현, 브루트포스 - 22251번: 빌런 호석

42.구현, 브루트포스 - 7490번: 0 만들기

업로드중..
43.구현, 조건 분기 - 7682번: 틱택토

(X가 먼저 수를 두고, 서로 번갈아 둔다.)종료 조건: 3칸 잇는 순간 종료, 게임판이 가득차도 종료.1) X, O가 동시에 우승하는 경우 -> invalid2) X 우승 시 -> 무조건 X 개수가 O 개수보다 1개 더 많아야 함 -> valid3) O 우승 시 ->
44.투포인터 - 2467번: 용액

0에 가장 가까운 값을 비교 및 저장 시 -> 절댓값으로 비교 및 저장하기!
45.그리디 - 2138번: 전구와 스위치

경우의 수: 1) 첫번째 스위치 누르지 않는 경우2) 첫번째 스위치 누르는 경우위 두 경우만 확인하면 그 이후 스위치는 직전 스위치 상태에 따라 자동으로 결정됨 (다르면 누르기)첫번째 스위치 누르지 않는 경우부터 확인해야 최소 횟수 먼저 찾을 수 있음
46.다익스트라 - 4485번: 녹색 옷 입은 애가 젤다지?

우선순위 힙을 사용하여 다익스트라 구현 -> 낮은 cost의 경로부터 탐색
47.투포인터 - 1253번: 좋다

48.이분 탐색 - 2110번: 공유기 설치

가능한 공유기 간 거리를 이분 탐색으로 찾아야 시간초과되지 않음
49.투포인터 - 1806번: 부분합

50.DFS, 백트래킹 - 1987번: 알파벳

dfs(maps, nx, ny, alphabets.union({maps\[nx]\[ny]}), level + 1) 이렇게 set.union({원소})로 넘기게 되면 매번 새로운 set을 만들어야 하므로 set 복사비용으로 인해 시간초과 발생함!\-> 그냥 add() 했
51.스택 - 9935번: 문자열 폭발

스택 외 다른 방식(ex. replace(), 중간 pop())으로 풀면 시간초과 발생함\-> 스택으로 풀면 O(N)만에 가능
52.슬라이딩 윈도우 - 13144번: List of Unique Numbers

슬라이딩 윈도우(set)로 연속 구간을 유지right을 늘려가며 값을 윈도우에 추가중복이 생기면 윈도우 내에 중복이 없을 때까지 left를 오른쪽으로 옮기면서 중복 제거윈도우 내에 중복이 없다면,right을 끝으로 하는 부분수열 개수 = (right - left + 1
53.그래프, BFS - 1976번: 여행 가자

travel0부터 BFS로 탐색하며 plans의 순서대로 도시를 pop해가며 진행cnt를 세어 n번 이상 돌았는데 계획을 pop하지 못하면 탐색 종료연결 여부보다 BFS 탐색 순서와 plans 순서 일치를 확인하는 방식여행 계획은 순서가 아니라 같은 연결 요소(그룹)인
54.수학, 브루트포스 - 1027번: 고층 건물

현재 idx 기준 왼쪽에 위치한 빌딩의 경우: m2 <= m 일 때 빌딩 i는 가려짐현재 idx 기준 오른쪽에 위치한 빌딩의 경우: m2 >= m 일 때 빌딩 i는 가려짐
55.브루트포스 - 2179번: 비슷한 단어

업로드중..
56.다중 BFS - 4179번: 불!
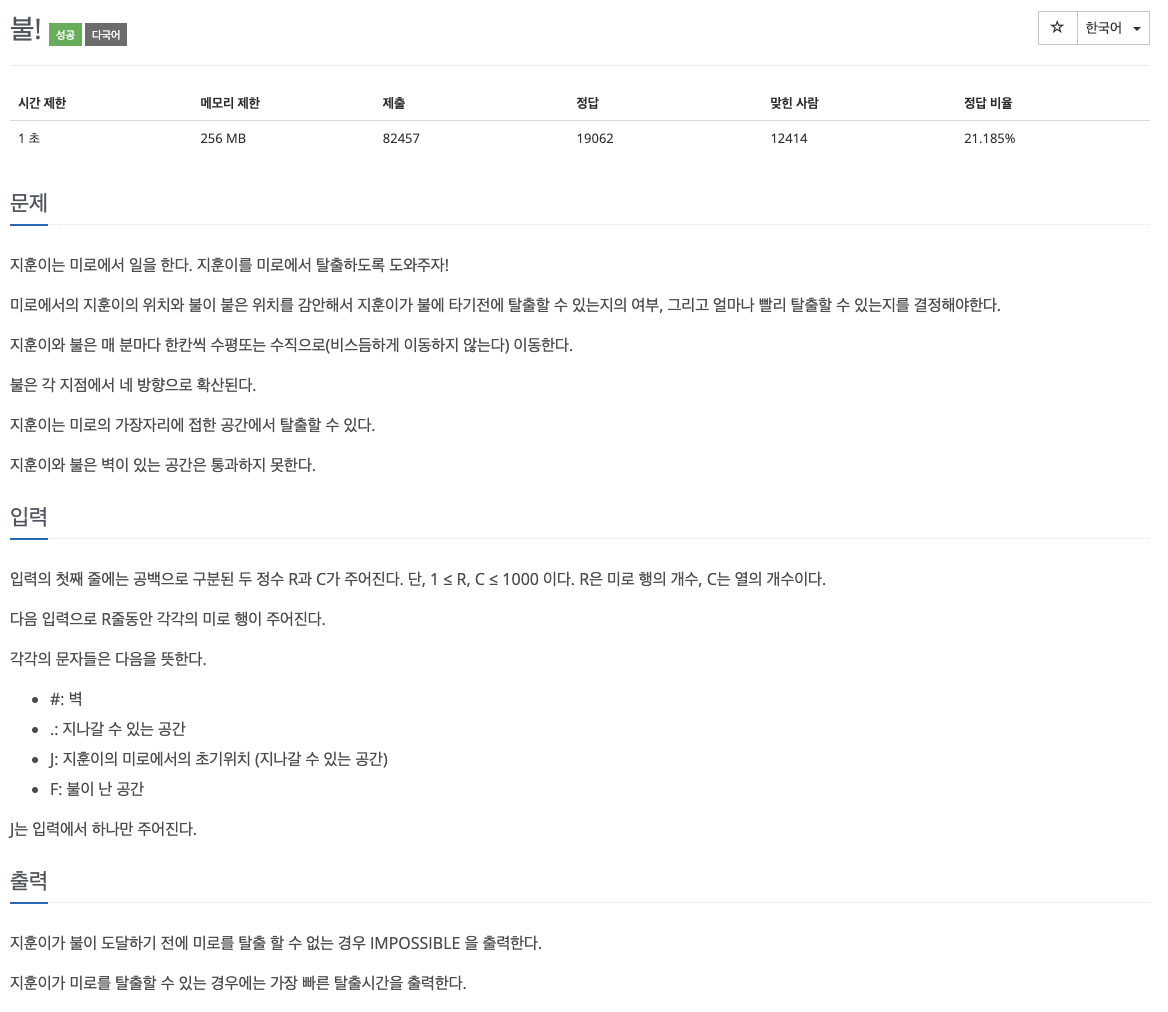
57.다익스트라, 그래프 - 1238번: 파티

: 모든 마을에서 X까지의 최단거리를 구할 때 각 마을에서 n번 실행하는 것은 비효율적이므로, 역방향 그래프에서 X에서 출발하여 모든 노드로 가는 최단거리를 구하면 모든 i -> X 거리를 한번에 계산할 수 있음
58.브루트포스 - 14658번: 하늘에서 별똥별이 빗발친다

: 격자 내에 트램펄린을 한 칸 씩 이동시키며 그 안에 별이 몇개 존재하는지 카운트하기 -> 시간초과 발생: 별 한 쌍의 좌표(하나는 가로 기준, 하나는 세로 기준으로 한 쌍)를 기준점으로 하여 트램펄린을 놓기 -> 별이 최소 1개 이상 있는 곳에만 트램펄린을 놓아보면
59.BFS - 16928번: 뱀과 사다리 게임

업로드중..모든 간선 가중치가 1 or 동일한 경우 -> BFS양의 가중치 -> 다익스트라가중치가 0 or 1 -> 0-1 BFS(deque 앞, 뒤로 삽입)
60.BFS - 1012번: 유기농 배추

61.구현, 큐 - 13335번: 트럭

62.LIS, DP - 2631번: 줄세우기

\-> 아이들 중 순서를 바꾸지 않고 그대로 둘 수 있는 최대 집합의 길이 구하기\-> 최장 증가 부분 수열(LIS) 구해서n - len(lis) 가 옮겨지는 아이의 최소 수가 됨!
63.BFS - 5014번: 스타트링크

64.누적합 - 2143번: 두 배열의 합

배열의 접두합 Pk는 A0부터 Ak−1까지의 누적합을 저장해 구간합을 O(1)에 계산할 수 있게 함!\-> 구간 A\[i:j]의 합은 P\[j] − P\[i] 한 번의 뺄셈으로 바로 얻을 수 있음A와 B의 모든 연속 부분합을 접두합으로 빠르게 뽑아내면 전체가 O(n²
65.LIS복원 - 14002번: 가장 긴 증가하는 부분 수열 4

tail과 tail_idx 배열로 “길이 k+1인 증가 수열의 최솟값 꼬리”와 그 위치를 관리새 값 x가 오면 bisect_left(tail, x)로 삽입 위치 pos를 찾아, 꼬리 추가 또는 교체prev_idx\[i] = tail_idx\[pos-1]로 각 원소가 연
66.DP, LIS - 2631번: 줄세우기

최소 교환 횟수 = 전체 아이들 수 - LIS 길이 (증가하는 부분 수열에 해당하는 아이들은 가만히 두고 그 외 아이들만 교환하면 되므로)
67.DP - 12865번: 평범한 배낭

한 아이템 중복 사용을 막기 위해 역방향으로, 중복 사용 가능 시 정방향!dp\[w]: 가방의 무게가 w일때 가질 수 있는 최대 가치점화식: dpw = max(dpw, dp\[w - weights\[i]] + values\[i])
68.LCS, DP - 9251번: LCS

1) 현재 비교하는 두 문자가 같으면 -> 이전 값(dpi - 1)에 + 1 해서 현재 값(dpi)에 저장dpi = dp\[i - 1]\[j - 1] + 12) 다르면 -> 두 문자 중 하나는 무조건 LCS에 들어갈 수 없으므로, s1i-1를 버리는 경우(dpi-1)와
69.DP - 15486번: 퇴사 2

dpi: i일 전까지 얻을 수 있는 최대 수익dpi = max(dpi, dpi-1)로 당일 상담을 안 했을 때 전일 수익을 받아오기상담 가능 기간(i + timesi)이 범위 안이면\-> dp\[i + times\[i]] = max(dp\[i + times\[i]],
70.메모이제이션 - 9184번: 신나는 함수 실행

메모 딕셔너리로 이미 계산된 w(a,b,c) 결과를 캐싱해 중복 호출을 방지!
71.이분 탐색 - 6236번: 용돈 관리

72.DP - 등굣길(Lv.3)

오른쪽(→)과 아래(↓) 이동만 허용하므로 총 이동 횟수는 항상 (n−1)+(m−1)로 고정됨!dpi에 (0,0)에서 (i,j)까지 올 수 있는 최단 경로 개수를 저장물웅덩이 칸은 dp=-10으로 표시해 계산에서 제외dp\[i]\[j] = dp\[i - 1]\[j] +
73.DP - N으로 표현(Lv.3)

업로드중..dpi는 N을 i번 써서 만들 수 있는 숫자들의 집합dpi를 만들기 위해 i를 j + (i - j)로 쪼개기dpj와 dpi - j에 있는 수들을 서로 사칙연산해서 dpi에 추가\-> 이렇게 하면 N을 i번 써서 만들 수 있는 모든 조합 구해짐목표 숫자가 dp
74.DP - 도둑질(Lv.4)

도둑 문제 유형(인접한 집은 동시에 X)은 해당 집 털거나 안털거나!\-> 점화식: dp\[i] = max(dp\[i - 1], dp\[i - 2] + money\[i])\-> dpi - 1: 이번 집 안털고 이전까지 최댓값 유지\-> dpi - 2 + moneyi:
75.DP - 정수 삼각형(Lv.3)

76.그래프 - 순위(Lv.3)

선수 i가 이길 수 있는 사람 수 + 질 수 있는 사람 수 = n−1이면 순위 확정 가능경기 결과를 그래프로 만들고, 정방향은 승리 관계, 역방향은 패배 관계로 저장A가 B를 이기고, B가 C를 이기면 → A가 C를 이긴다(전이성)는 것을 이용!BFS로 정방향 탐색 →
77.그리디, 프림 - 섬 연결하기(Lv.3)

우선순위 큐(heap)에서 비용이 가장 작은 간선을 꺼내 방문하지 않은 노드를 선택선택한 노드를 MST(Minimum Spanning Tree, 최소 신장 트리)에 포함시키고, 그 노드에서 나가는 간선들을 큐에 추가모든 노드를 방문할 때까지 반복해 MST의 총 비용을
78.힙 - 디스크 컨트롤러(Lv.3)

79.그래프 - 가장 먼 노드(Lv.3)

80.해시 - 베스트 앨범(Lv.3)

81.이분탐색 - 입국심사(Lv.3)

82.다익스트라 - 2211번: 네트워크 복구

모든 노드를 연결하되, 간선 가중치 합이 최소가 되도록 만드는 트리출발 노드라는 개념이 없음ex) 전체 네트워크 구축 비용을 최소화하고 싶을 때\-> MST의 경로는 “최단 경로”를 보장하지 않음!특정 시작점(여기서는 1번)에서 모든 노드까지의 최단경로만 모은 트리다익
83.DFS, BFS - 1260번: DFS와 BFS

84.그래프 - 11724번: 연결 요소의 개수

85.두개의 큐 BFS - 3197번: 백조의 호수

업로드중..
86.BFS, 구현 - 16236번: 아기 상어

87.BFS, 트리 - 1167번: 트리의 지름

1) 트리에서 임의의 정점 s에서 가장 먼 정점 a를 찾기2) 이 a는 지름 경로의 한 끝점!3) 다시 a에서 BFS를 돌려 가장 먼 정점과 그 거리를 구하기 -> 이때의 가장 먼 거리가 트리의 지름\-> BFS 2번으로 O(N)에 해결 가능함!
88.DP - 2293번: 동전 1

1) dp\[x]: 현재까지 고려한 동전으로 x원을 만드는 조합(순서무시)의 개수2) 초기값: dp\[0] = 1 (아무 동전도 안 쓰는 1가지 경우)3) 루프 순서: 동전 바깥, 금액 오름차순 (조합 + 무한사용)4) 점화식 : dp\[value] += dp\[val
89.완전탐색, BFS, 구현 - 17135번: 캐슬 디펜스

리스트에 튜플 형태로 저장 시 각 값의 저장 순서 주의하기여러 경우의 수에 대해 시뮬레이션하는 경우 매 턴마다 입력받은 맵을 deepcopy해서 써야 함while문 종료 조건에 들어간 변수 매번 갱신 주의
90.LIS, 이분탐색 - 2352번: 반도체 설계

선이 교차하지 않아야 함 -> 순서 유지 -> 최대한 많은 연결 -> 최장증가부분수열의 길이 구하는 문제!
91.그리디 - 1744번: 수 묶기

2 이상의 양수: 가장 큰 수부터 오름차순 정렬 순서대로 다음 숫자와 곱해서 더하기1: 전부 더해주기0 또는 음수: 가장 작은 수부터 오름차순 정렬 순서대로 다음 숫자와 곱해서 더하기
92.다익스트라, 우선순위 큐 - 1753번: 최단경로

93.최대 다익스트라 - 1939번: 중량제한

dist\[v] = 시작점→v까지 경로 중 최소 간선값의 최댓값시작점은 제약이 없으므로 dist\[start] = float('inf') 로 두고 최대 힙(음수화)으로 탐색하기힙에서 꺼낸 weight보다 작은 구버전 경로는 무시하기이웃 탐색 시 new_w = min(w
94.구현, BFS - 2573번: 빙산

빙산 녹이기: 매 해마다 ices 좌표 기준으로 사방의 바다 개수를 세고, 한꺼번에 높이를 줄여 동시 갱신하기분리 여부 확인: bfs()로 빙산 덩어리 크기와 전체 빙산 개수를 비교해, 다 닿지 못하면 분리된 것으로 판정하기시작 시 이미 분리된 경우 0 출력, 아니면
95.브루트포스 - 1107번: 리모컨

permus = list(permus) -> 제너레이터를 list로 변환하면 모두 메모리에 올라가서 메모리 초과남 주의!! list 변환 없이 제너레이터 그대로 순회하면 됨!elem_cnt = abs(N - num) + i -> 두 수의 차이(+ or - 눌러야 하는
96.시뮬레이션, BFS - 메두사와 전사

97.벨만-포드 - 11657번: 타임머신

음수 가중치의 간선이 있을 때의 최단경로 문제 -> 벨만-포드 알고리즘사이클 없는 최단경로는 최대 V-1개의 간선만 포함함완화 연산: if dist\[v] > dist\[u] + w 거리가 더 짧아지면 갱신!V-1번 완화해서 모든 최단경로 구하기V-1번 후에도 최단경로
98.시뮬레이션, BFS - 미지의 공간 탈출

get_exit()로 시간의 벽의 출구의 방향 및 좌표를 얻고, 출구가 있는 면엔 0,1,1,..., 나머지 면엔 1,1,...를 M번째 행으로 추가하기warp(nr,nc,side)로 경계 이탈 시 면 이동 및 좌표 변환하기, 경계 이탈하지 않으면 그대로 (nr,nc,
99.다익스트라 - 1504번: 특정한 최단 경로

경로는 1→V1→V2→N, 1→V2→V1→N 두 가지 경우만 고려하면 됨!다익스트라는 dijkstra(1), dijkstra(V1), dijkstra(V2) 총 3번만 돌리면 구할 수 있음
100.BFS, 시뮬레이션 - 마법의 숲 탐색

101.프림 - 1368번: 물대기

각 논에 우물 파는 비용을 “가상 정점에서 논으로 가는 간선”으로 초기 힙에 모두 삽입하기 (우물 비용 가장 싼 논에서 시작하는 걸로 하면 틀림! MST가 하나만 존재하는게 아니기 때문에)힙에서 가장 싼 비용을 꺼내 방문하지 않은 논을 선택, 전체 비용 누적선택된 논에
102.BFS, 시뮬레이션 - 고대 문명 유적 탐사

1) 시계방향 90도 회전output_arr = list(map(list, zip(\*input_arr\[::-1])))2) 180도 회전output_arr = \[a\[::-1] for a in input_arr\[::-1]]3) 270도 회전output_arr =
103.시뮬레이션 - 루돌프의 반란

항상 조건문 쓸 때는 발생가능한 모든 경우의 수를 elif로 틀을 다 만들어 둔 후, 각각의 경우의 수 안으로 들어가기while True 쓸 때는 어떤 조건에서 break 걸어야 하는지 꼼꼼히 체크dx dy를 두개 이상 만드는 경우, 다른 dx dy랑 헷갈리지 않게 주
104.시뮬레이션, DFS - 왕실의 기사 대결

재귀 구현 시, for문 안에서 재귀함수 호출할 때 값 여러개 리턴되는데 하나의 변수에 다 할당하는 실수 주의하기move_knight()에서 실수하지 않기이미 다른 기사가 한번 밀었던 기사라면 패스(하나당 한 번만 밀어야 함)!! 면적이 w x h이므로 맞닿은 기사가
105.BFS, 이분 그래프 - 1707번: 이분 그래프

BFS + 색칠: 인접한 노드를 0과 1로 번갈아 색칠하며 탐색충돌 검사: 같은 색의 노드가 인접하면 즉시 False 반환중복 방지: 큐에 넣을 때 바로 colorsc 설정하여 중복 삽입 차단연결 요소 처리: 1~V까지 순회하며 끊어진 그래프도 모두 검사시간복잡도: O