타원곡선 암호(ECC)는 공개키 암호화 방식 중 하나로 데이터 암호화, 디지털 인증 등 현재 가장 많이 쓰이는 암호방식이다.
RSA 암호방식과 달리 이산로그 문제에 착안해 만들어졌다.
RSA는 암호키 길이가 길어지면 보안 강도는 높아지지만 속도가 느려진다.
하지만 ECC를 사용하면 짧은 키로도 동일한 암호 성능을 가지는데, 이는 컴퓨터 성능이 낮아도 암호 성능을 유지할 수 있게 하였다. 256비트의 ECC키는 3072비트의 RSA키와 비슷한 암호화 레벨이며 키 값이 커질수록 RSA보다 암호화 레벨이 급격하게 높아진다.
타원 곡선
식을 만족하는 x, y의 집합을 곡선 그래프로 나타낸 것이다.
타원곡선 그래프는 x축을 중심으로 대칭되며, 비 수직선에 대해 최대 3개 지점에서 곡선과 교차한다는 특징을 가지고 있다.

타원 곡선 상에서의 연산
타원 곡선을 이용한 암호화 알고리즘을 알기 위해서는 타원 곡선 상의 덧셈 연산을 이해해야 한다.
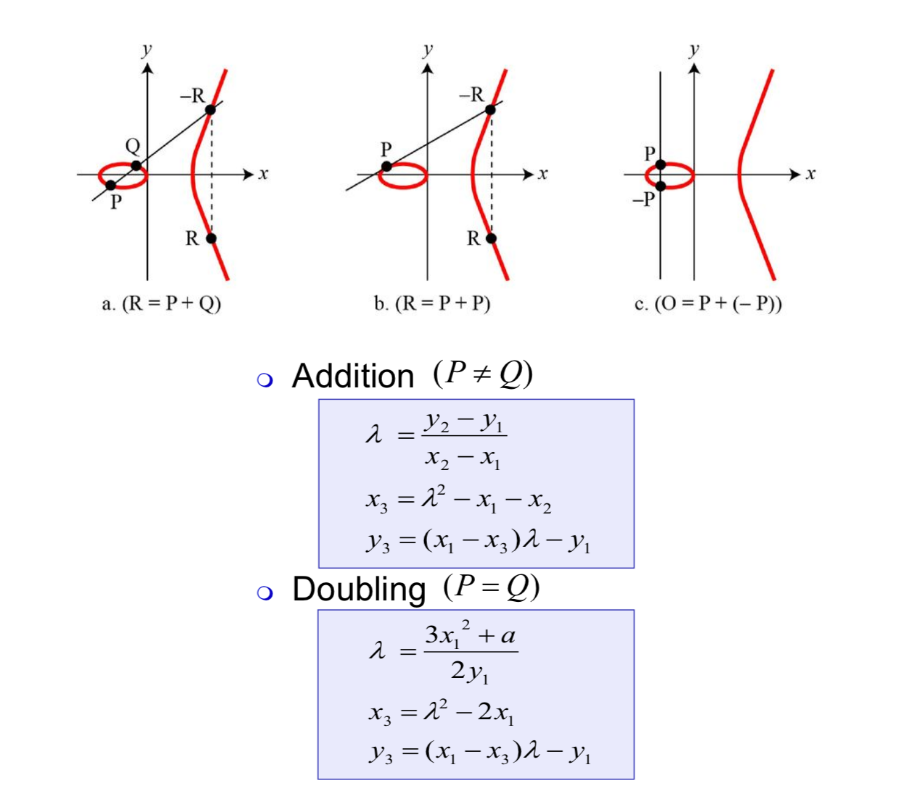
간단한 예시로 타원 곡선 상의 P와 Q의 덧셈 연산을 설명하자면, P와 Q를 지나는 직선이 타원과 만나는 교점(-R)을 x축으로 대칭시킨 점을 P + Q = R로 정의한다.
아래 그림의 그래프(b)는 같은 값을 가지고 있는 P를 구하는 타원 곡선이다.
덧셈 연산과 같이 P의 접점을 타원 곡선으로 이은 교점(-R)을 x축으로 대칭시킨 점을 2P = R로 정의한다.
유한에서의 타원 곡선
유한체는 유한개의 원소를 가지는 체를 뜻한다. 타원 곡선을 이용해서 암호화에 적용하려면 유한한 자연수 범위에서 덧셈연산도 역으로 추적하기 어려워야 한다. 타원 곡선 암호는 모든 점들을 큰 소수 p에 대한 나머지들, 즉 𝔽p 내에 존재한다. 만약 𝔽p에서 점 P(x, y)가 타원곡선 E에 있다면 x, y는 모두 소수 p의 나머지들이고 타원 곡선 식도 mod p에서 만족하면 된다.
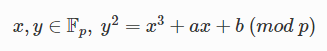
𝔽p에서 덧셈연산과 스칼라 곱 계산을 통해 얻은 타원 곡선 위의 점들은 이산로그 문제가 된다.
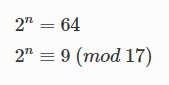
이를 더 간단히 설명하자면 첫 번째 식의 n값은 6으로 쉽게 구할 수 있지만 mod 17에서 2의 배수 중 9가 되는 값은 일일히 계산해보지 않는 이상 어렵다.
타원 곡선 점들도 이와 같이 몇 번의 덧셈연산으로 결과 값을 구하긴 쉽지만 기준 점으로부터 몇 번의 연산을 했는지는 구하기 매우 어렵다. 타원 곡선 암호란 어려운 몇 번의 덧셈을 해야하는지 위에 이산로그 문제에서 지수가 되는 부분을 비밀키로 하고 그 결과가 되는 점을 개인키로 한다.
ECC 알고리즘 키 생성
G: 생성자, 타원 곡선 상의 임의의 점
x: 개인키, P보다 작은 소수(Prime)로, 난수 생성기로 생성
Q: 공개키, 개인키로부터 연산
점 P=(x, y)가 타원 곡선 상에 위치해 있을 때 두 점 P, Q와 임의의 정수 x에 대해 다음과 같은 방정식을 정의할 수 있다.
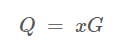
이때 x의 값을 구하는 것이 타원 곡선 이산대수 문제인데, 공개키 Q는 Q=xG = G + G + … + G으로 G를 x번 덧셈한 값이다.
Q = xG 수식에서 x와 G를 이용하여 Q를 구하기 쉽지만, 알려진 G값과 Q값을 통해 x 값을 구하기 어려운 점을 이용한다.
이러한 것을 ECDLP(Elliptic Curve Discrete Logarithm Problem)라고 부르며, 이러한 속성으로 인해 공개키 암호기술로 사용된다. ECC의 덧셈연산에서 P를 doubling한 2P를 보면 2G = G + G는 점 G에서의 접선이 타원 곡선과 만나는 점을 x축으로 대칭시킨 지점이다.
4G = 2G + 2G는 2G에 해당하는 점에서 마찬가지로 접선을 그어 타원 곡선과 만나는 점의 x축 대칭 점이다. G의 상수 배 연산은 이를 반복적으로 수행할 수 있다.
아래의 주어진 식으로
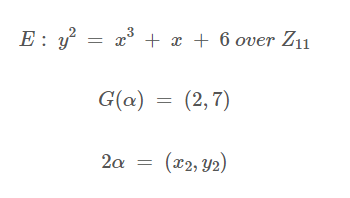
2α를 구한다면,
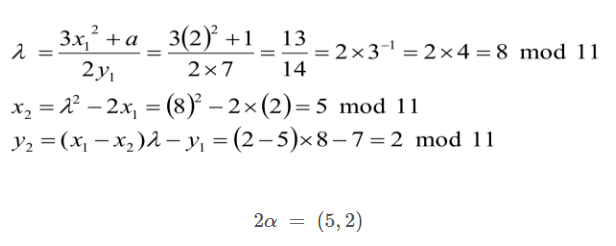
이 방법을 이용하여 α, 2α, ... , kα를 구할 수 있다.
비밀키(x) * α = 공개키(Q)
ECC를 이용할 때 주의할 점
난수 생성기의 중요성 RSA에 비교한 ECC의 약점은, 사용되는 개인키의 bit수가 적다는 것이다. 개인키는 난수 생성키를 통해서 만들어지기 때문에, 품질이 떨어진 난수 생성기를 사용할 경우 공격자에 의해 개인키가 예측될 수 있다고 한다.
ECDSA 암호 알고리즘의 보안은 개인키의 보안에 의해 좌우 되므로, 개인키를 예측할 수 없도록 랜덤하게 생성해야 한다. 즉 예측할 수 없는 랜덤한 수를 가지고 개인키를 생성해야 한다.
