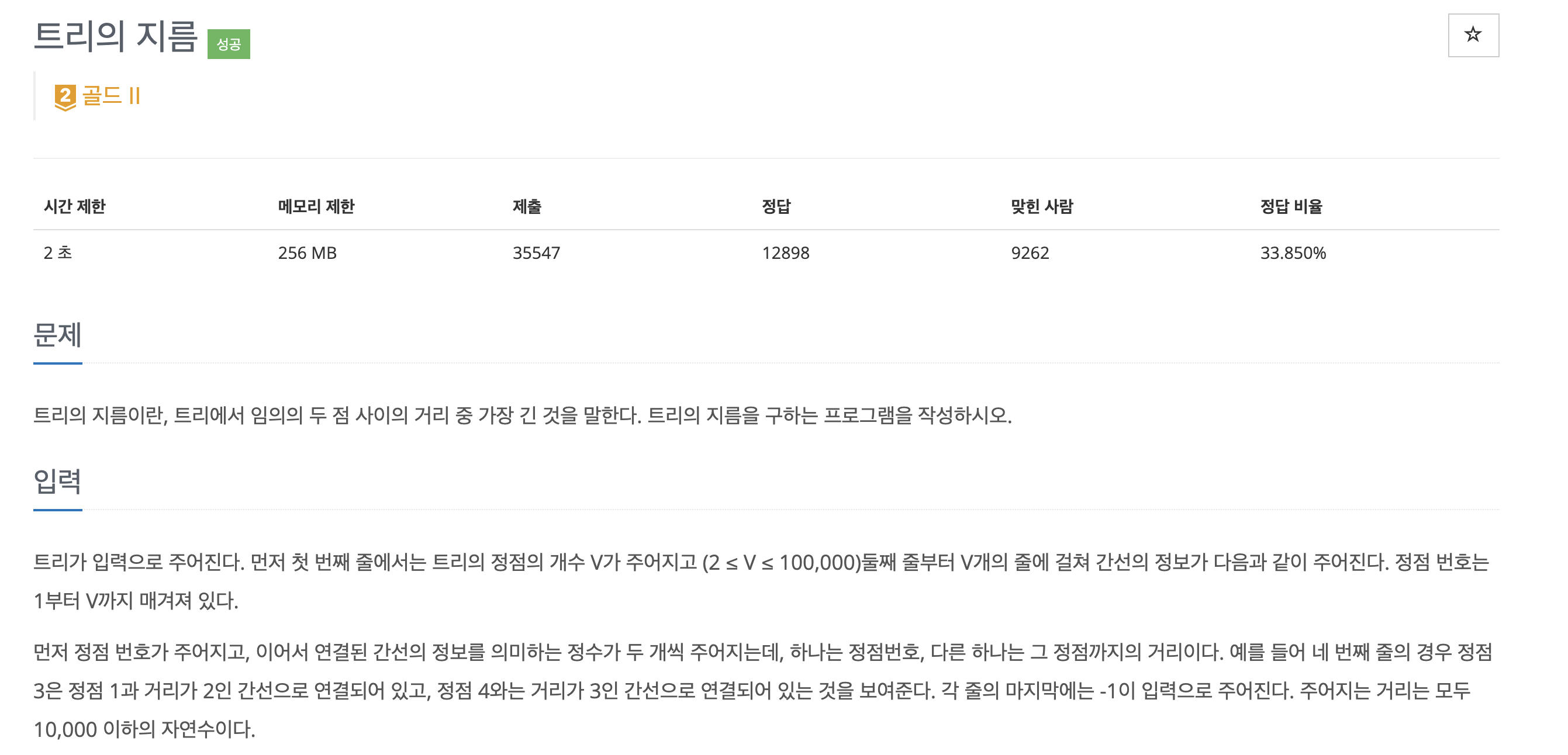
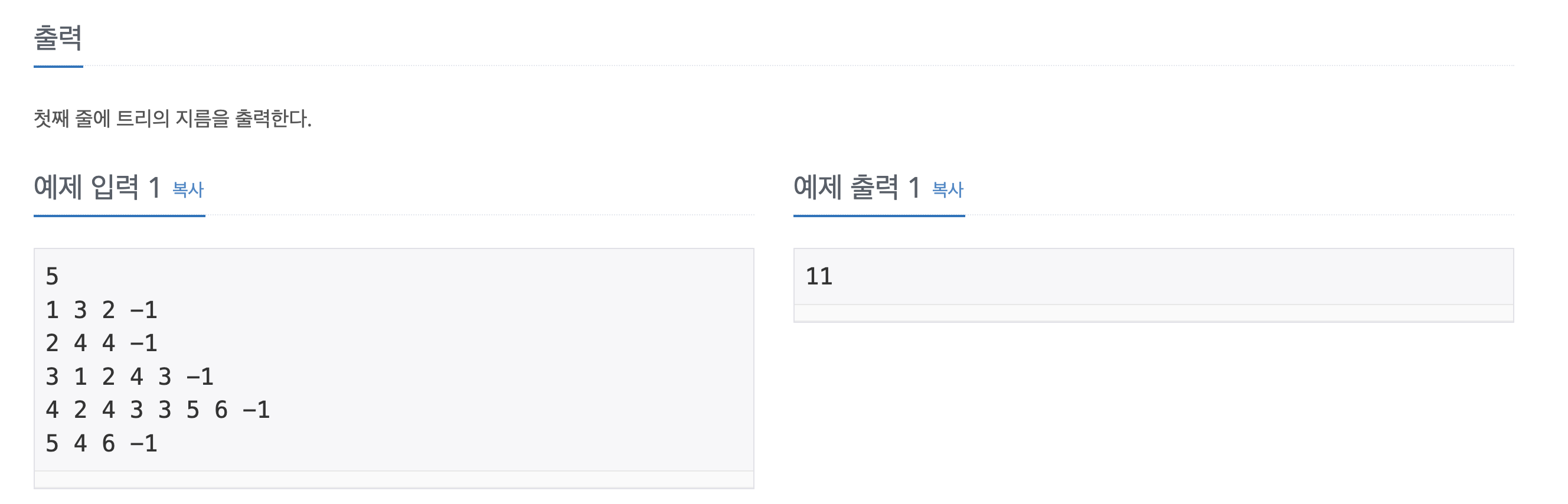
🌱 문제
🌱 풀이
처음 푼 과정
- 처음에는 어떻게 풀어야 할지 감이 안와서 완전탐색의 방법밖에 떠오르지 않았다.
- 모든 정점을 시작정점으로 지정하여 BFS를 돌리고, 한번 BFS를 돌릴때 마다 시작정점에서 가장 먼 정점까지의 거리 값을
answer에 저장해 주었다.
- 하지만 이 방식은 시간초과가 발생했다.
(2 ≤ V ≤ 100,000)이므로 BFS를 N만 큼 반복하면 N^2만큼의 시간복잡도가 발생하기 때문에 당연한 결과였다. (100,000 x 100,000)
틀린코드 (BFS)
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.Queue;
import java.util.StringTokenizer;
public class Main {
static class Node{
int to;
int cost;
public Node(int to, int cost) {
this.to=to;
this.cost=cost;
}
}
static int V;
static ArrayList<Node> edges[];
static boolean visit[];
static int dist[];
static int answer;
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
V=Integer.parseInt(br.readLine());
edges = new ArrayList[V+1];
dist = new int[V+1];
visit = new boolean[V+1];
for(int i=0; i<=V; i++) {
edges[i]= new ArrayList<Node>();
}
for(int i=0; i<V; i++) {
st = new StringTokenizer(br.readLine());
int vertex = Integer.parseInt(st.nextToken());
while(true) {
int next = Integer.parseInt(st.nextToken());
if(next==-1)
break;
int cost = Integer.parseInt(st.nextToken());
edges[vertex].add(new Node(next,cost));
}
}
for(int i=1; i<=V; i++) {
bfs(i);
}
System.out.println(answer);
}
static public void bfs(int start) {
Queue<Node> queue = new ArrayDeque<Node>();
dist = new int[V+1];
visit= new boolean[V+1];
queue.add(new Node(start,0));
visit[start]=true;
dist[start]=0;
while(!queue.isEmpty()) {
Node cur = queue.poll();
for(int i=0; i<edges[cur.to].size(); i++) {
int next = edges[cur.to].get(i).to;
int cost = edges[cur.to].get(i).cost;
if(visit[next])
continue;
visit[next]=true;
dist[next]=dist[cur.to]+cost;
queue.add(new Node(next, cost));
}
}
for(int i=1; i<=V; i++) {
answer=Math.max(dist[i],answer);
}
}
}
다시 풀어보자
- 도저히 모르겠어서 구글링을 통해 도움을 받았다.
- 가장 긴 거리를 갖는 두 정점을 각각
vertex1, vertex2라고 하자.
- 이때, 어떤 임의의 정점에서 가장 긴 거리를 구한다면, 그 거리는 임의의 정점과
vertex1 또는 vertex2 사이의 거리 라는 규칙을 발견할 수 있다.
- 그렇기 때문에 임의의 한 정점에서 가장 먼 정점을 구하고, 그 정점에서부터 가장 먼 정점사이의 거리가 트리의 지름이 된다.
- 임의의정점(1)에서 DFS를 통해 가장 먼 정점을 구하고, 그 정점에서 다시 DFS를 돌려서 가장 먼 정점까지의 거리를 구했다. (이 과정은 BFS도 상관 없을 것이라 생각된다)
의문점
- 구글링을 통해 방법은 찾았지만, 위 방법이 확실히 반례가 없는건지 와닿지가 않았다. 그래서 좀 더 찾아보았다.
- 트리에서는 한 정점에서 다른정점까지의 경로가 유일하다.
- 임의의 각 정점에서 가장 먼 정점까지의 경로를 살펴보면 항상 일부가 겹치게 된다.
-> 그렇기 때문에 임의의 정점에서 가장 먼 정점은 트리의 지름을 연결하는 두 정점중 하나에 해당하게 되는 것이다.
- 처음엔 와닿지 않았지만, 구글링을 통해 반례를 살펴보면서 이해하니까 어느정도 이해가 되었다. (비슷한 문제를 더 풀어봐야겠당)
🌱 정답 코드
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.ArrayDeque;
import java.util.ArrayList;
import java.util.Queue;
import java.util.StringTokenizer;
public class Main {
static class Node{
int to;
int cost;
public Node(int to, int cost) {
this.to=to;
this.cost=cost;
}
}
static int V;
static ArrayList<Node> edges[];
static boolean visit[];
static int candidate;
static int answer;
static int max;
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
V=Integer.parseInt(br.readLine());
edges = new ArrayList[V+1];
visit = new boolean[V+1];
for(int i=0; i<=V; i++) {
edges[i]= new ArrayList<Node>();
}
for(int i=0; i<V; i++) {
st = new StringTokenizer(br.readLine());
int vertex = Integer.parseInt(st.nextToken());
while(true) {
int next = Integer.parseInt(st.nextToken());
if(next==-1)
break;
int cost = Integer.parseInt(st.nextToken());
edges[vertex].add(new Node(next,cost));
}
}
dfs(1,0);
visit=new boolean[V+1];
dfs(candidate, 0);
System.out.println(max);
}
static public void dfs(int v, int len) {
if(len>max) {
max=len;
candidate=v;
}
visit[v]=true;
for(int i=0; i<edges[v].size(); i++) {
Node next = edges[v].get(i);
if(visit[next.to]==false) {
dfs(next.to,len+next.cost);
}
}
}
}
참고한 블로그
https://moonsbeen.tistory.com/101


