[프로그래머스/java] 스터커 모으기(2)

문제 링크 - https://school.programmers.co.kr/learn/courses/30/lessons/12971?language=java

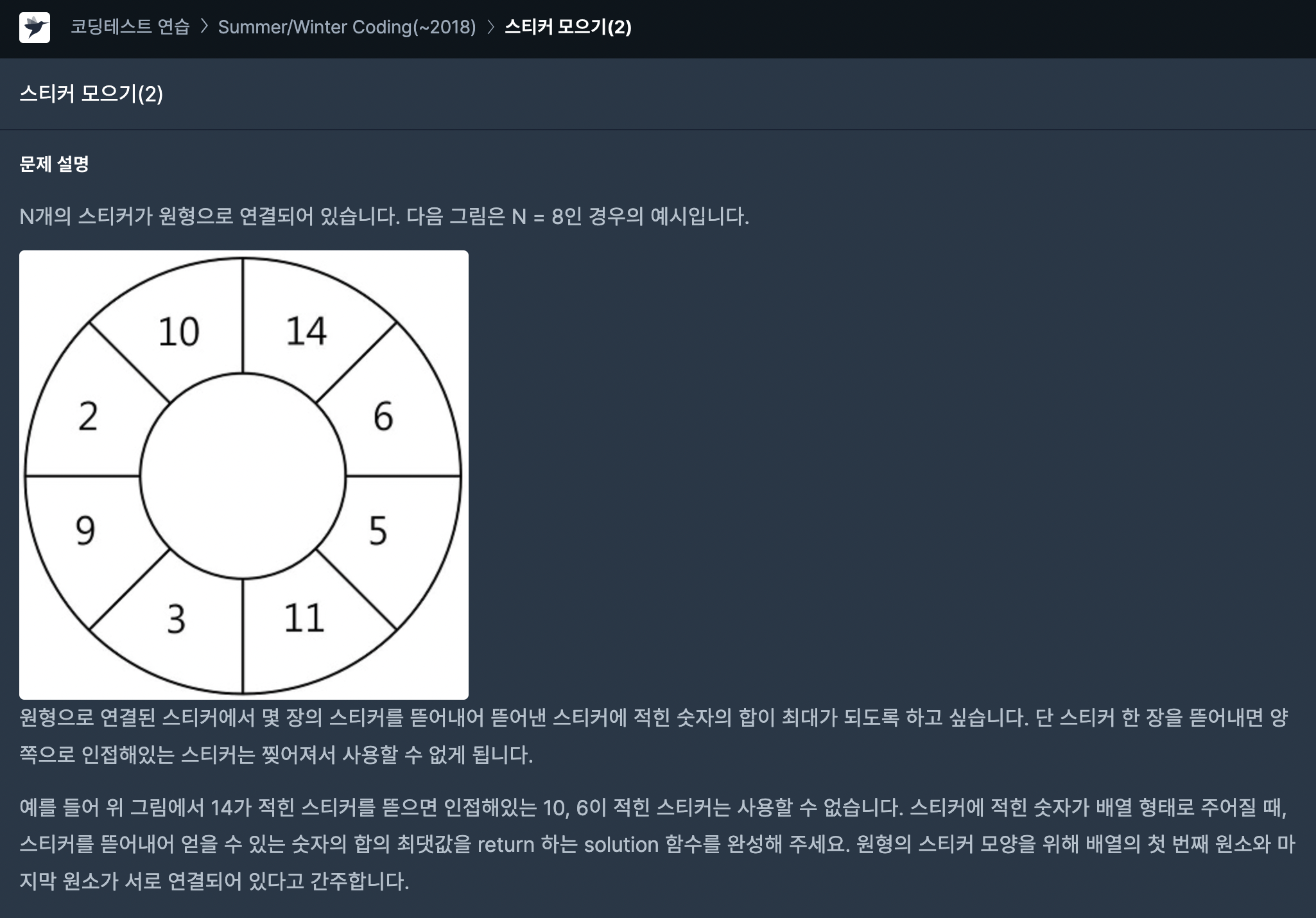
🌱 문제

🌱 풀이

• 어떻게 풀어야 할지 고민하다가 dp로 푸는 방식이 생각 났다.
• 우선 원형 스티커를 일차원 배열이라고 가정하고 풀기로 했다. 원형스티커 이기 때문에 두가지 경우로 나누어 생각하였다.
  1. 첫번째 스티커를 포함한 경우 (=마지막 스티커를 포함하지 않을 경우)
2. 첫번째 스티커를 포함하지 않을 경우 (=마지막 스티커를 포함할 경우)
• 각각의 경우에 dp[], dp2[] 배열을 채우고, 마지막에 두 dp배열의 마지막 값 중 더 큰 값으로 정답을 리턴해 주었다.
• 이때 dp[i]의 정의는 0번째부터 i번째 스티커 까지 고려 하였을 때 답이 되는 최댓값이다.
• i>=2 일때 dp[i]=Math.max(dp[i-1],dp[i-2]+sticker[i]) 로 나타낼 수 있다. (스티커를 연속해서 포함할 수 없으므로 전전 최댓값에+현재스티커 합한 값이 최대가 되거나 바로 직전의 최댓값이 그대로 최댓값이 되거나 둘중 하나이다)
• 테스트케이스가 몇개 틀린게 있었는데, 주어진 스티커가 1개 일때를 생각하지 못했었다.

🌱 코드

class Solution {
    int dp[];
    int dp2[];
    public int solution(int sticker[]) {
        int answer = 0;
        int n =sticker.length;

        //원형 스티커를 1차원 배열로 생각
        dp=new int[n];
        dp2=new int[n];
        
        if(n==1)
            return answer=sticker[0];
        
        //맨 처음 스티커 포함한 경우
        dp[0]=sticker[0];
        dp[1]=sticker[1];
        
        for(int i=2; i<n-1; i++){ // 마지막 스티커는 포함할수 없으므로 i<n-1 까지 반복
            dp[i]=Math.max(dp[i-1],dp[i-2]+sticker[i]);
            answer=Math.max(dp[i],answer);
            // System.out.println("answer1: "+answer);
        }
        //맨 처음 스티커 포함하지 않은 경우
        dp2[0]=0;
        dp2[1]=sticker[1];
        for(int i=2; i<n; i++){
            dp2[i]=Math.max(dp2[i-1],dp2[i-2]+sticker[i]);
            answer=Math.max(dp2[i],answer);
            // System.out.println("answer2: "+answer);
        }

        return answer=Math.max(dp[n-1],dp2[n-1]);
    }
}