RNN (Recurrent Neural Network)

dandan·2025년 9월 11일

AI

목록 보기

3/3

들어가며...

요즘은 Vanilla RNN을 직접 쓰는 경우가 거의 없다. 긴 의존 관계를 제대로 학습하지 못하고, 역전파 과정에서 기울기가 소실·폭발하는 문제까지 안고 있기 때문이다. 대신 Transformer가 사실상 모든 시퀀스 처리 문제의 표준으로 자리 잡았다.

그럼에도 RNN을 건너뛰어버리면 Transformer가 왜 혁신이었는지 맥락을 놓치기 쉽다. 은닉 상태를 이용해 과거 정보를 이어가는 순환 신경망의 발상은 이후 LSTM, GRU 같은 변형 모델로 이어졌고, 결국 Transformer의 아이디어와도 비교되는 출발점이 된다.

이번 글에서는 우선 기본 RNN의 구조와 동작 방식을 살펴본다. 이를 통해 순환 구조의 장단점을 이해하고, 이어질 글에서 LSTM과 GRU를 다루며 Transformer가 왜 필요했는지를 더 분명히 드러내고자 한다.

State-Space Model as RNN

State-Space Model의 관점에서 RNN을 이해해보자.

First Order System

1. $x_t=f(x_{t-1})$

현재 시간의 상태가 이전 시간의 상태와 관련이 있다고 가정한다.

$x$ : 상태 (시세, 날씨, 점수)
$t$ : 시간
$x_t$ : t일 때의 상태

이 시스템은 외부 입력 없이 자기 혼자서 돌아가는 autonomous system 이다.

2. $x_t=f(x_{t-1}, u_t)$

현재 시간의 상태 $x_t$ 가 이전 시간의 상태 $x_{t-1}$ 와 현재의 입력 $u_t$ 에 관련이 있다고 가정한다.

$x$ : 상태
$u$ : 입력

State-Space Model

1차원 시스템의 모형 $x_t=f(x_{t-1}, u_t)$ 에서 $x_t$ 의 관측 가능성을 따져보자.

모든 시간 t에서 모든 상태 $x_t$

ANN과의 가장 큰 차이는 시간에 따라 변화하는 Weight를 공유한다는 것이다.

시퀀스 데이터란?

시퀀스 데이터(sequence data)는 순서가 중요한 데이터를 말한다.

텍스트: 단어의 순서에 따라 문장의 의미가 달라짐
음성: 시간 축에 따라 신호가 이어짐
주가·날씨 같은 시계열 데이터: 앞뒤 맥락에 따라 패턴이 정해짐
영상: 프레임이 순서대로 쌓여야 의미가 유지됨

일반적인 MLP는 입력을 독립적으로 처리하기 때문에 이런 순서를 직접 고려하지 못한다. 반면 RNN은 은닉 상태를 통해 이전 시점의 정보를 현재로 전달하여 순서와 맥락을 학습할 수 있다.

RNN 아키텍처 유형

RNN은 시퀀스를 어떻게 입력·출력하느냐에 따라 네 가지 대표 구조로 나뉜다.

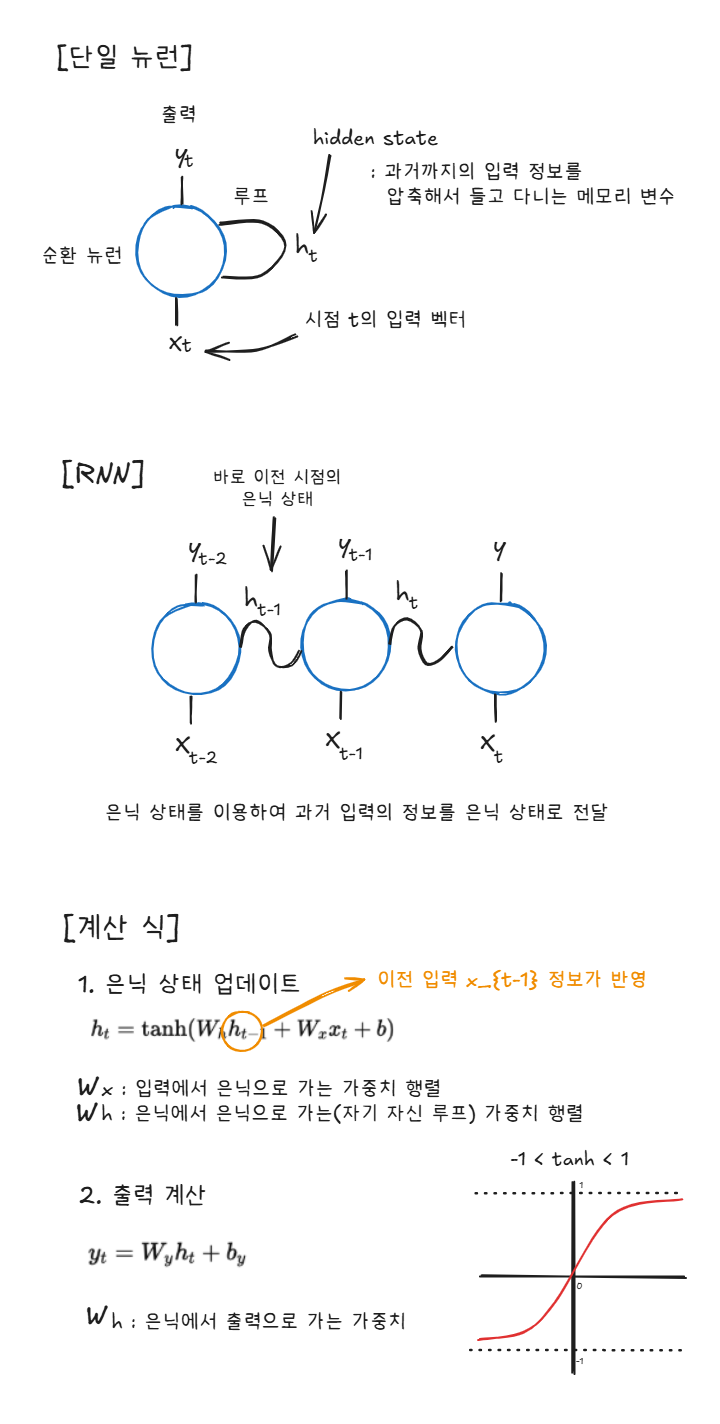
RNN

RNN은 Recurrent Neural Network로 순환 신경망을 말한다. 이는 시게열이나 연속적인 데이터를 다룰 때 사용된다. CNN이나 MLP 등 다른 신경망의 경우는 입력을 한번 처리하고 끝난다. 즉 현재 입력만 보고 예측하는 여타 신경망과는 다르게 RNN의 경우 과거의 정보를 기억하여 다음 계산에 반영하는 구조를 갖는다. 이는 자연어와 같이 데이터의 순서가 중요한 경우 적절하게 사용될 수 있다. 다만 Vanilla RNN의 경우는 Long-Term Dependency(장기 의존성) 문제를 갖는다. 이를 극복하기 위해 LSTM, GRU가 나오게 되었다.

RNN은 어떻게 과거의 정보를 반영할까? RNN의 구조를 간단히 알아보며 RNN의 동작 원리와 학습 과정에서의 장기 의존성 문제의 발생 원인을 이해해보도록 하자.

Long-Term Dependency

RNN의 동작 원리를 살펴보면, 왜 장기 의존성 문제가 발생하는지 이해할 수 있다.

은닉 상태의 업데이트 수식은 다음과 같다.

$h_t = \tanh(W_h h_{t-1} + W_x x_t + b)$

여기서 $h_t$ 는 이전 은닉 상태 $h_{t-1}$ 을 거쳐 반복적으로 계산된다. 즉, 은닉 상태는 본질적으로 순환 구조(루프)를 갖는다.

이제 출력 손실 $L$ 에 대한 과거 은닉 상태의 기여도를 따져보자.

그래디언트 $\frac{\partial L}{\partial h_{t-k}}$ 는 체인 룰에 따라 시점마다 곱해지며 전달된다. 결국 반복적으로 같은 행렬 곱이 누적된다는 뜻이다.

곱의 누적을 아래처럼 표현할 수 있다.

\frac{\partial L}{\partial h_t} \cdot \prod_{i=1}^{k} \frac{\partial h_{t-i+1}}{\partial h_{t-i}}=\frac{\partial L}{\partial h_{t-k}} = \frac{\partial L}{\partial h_t} \cdot \frac{\partial h_t}{\partial h_{t-1}} \cdot \frac{\partial h_{t-1}}{\partial h_{t-2}} \cdots \frac{\partial h_{t-k+1}}{\partial h_{t-k}}

이와 같이 곱셈이 누적되는 구조에서는 항의 크기가 1보다 작으면 곱이 점점 0으로 수렴하여 그래디언트 소실(Gradient Exploding) 문제가 발생하고, 1보다 크면 기하급수적으로 커져 그래디언트 폭발(Gradient Exploding)이 일어난다.

RNN 모델과 이미지 분류

이미지 분류 문제에서 CNN은 공간적 구조를 직접 반영하기 때문에 가장 우수한 성능을 낸다. 하지만 작은 이미지를 다루는 경우라면 MLP나 RNN도 충분히 적용할 수 있다. 일반적인 MLP는 평탄화된 픽셀만을 독립적으로 처리하기 때문에 공간 정보를 활용하지 못한다. 반면 RNN은 입력을 순차적으로 처리하면서 은닉 상태에 이전 시점의 정보를 저장할 수 있다는 특징이 있다.

따라서 64×64 이미지를 행 단위로 잘라 순차적으로 입력하면, CNN처럼 명시적으로 공간 구조를 반영하지 못하더라도 RNN은 “행의 순서”를 기억함으로써 어느 정도 공간적 맥락을 학습할 수 있다. 이 덕분에 RNN은 단순 MLP보다 이미지 분류 성능에서 더 나은 결과를 낼 수 있다.

RNN Model

PyTorch로 간단한 다층 RNN 분류기를 정의해보았다.

class RNNModel(nn.Module):
    def __init__(self, input_dim, hidden_dim, layer_dim, output_dim):
        super().__init__()
        self.hidden_dim = hidden_dim      # 각 시점 은닉벡터의 차원 크기
        self.layer_dim  = layer_dim       # RNN 층 수(스택 개수)

        # 내부 파라미터(W_ih, W_hh, b_ih, b_hh)는 self.rnn 안에 자동 등록됨
        self.rnn = nn.RNN(
            input_size=input_dim,     # 입력 벡터 크기
            hidden_size=hidden_dim,   # 은닉 상태 차원
            num_layers=layer_dim,     # RNN을 몇 층 쌓을지
            batch_first=True          # 입력 차원 순서: (배치, 시퀀스 길이, 특성)
        )
        # 마지막 은닉 벡터를 원하는 출력 차원으로 바꿔주는 역할
        self.fc = nn.Linear(hidden_dim, output_dim)

    def forward(self, x):
    
        # rnn은 시작할 때 초기 은닉 상태(h0)이 필요하기에 0으로 채움
        # h0 : (num_layers, batch, hidden_dim)
        # 매 forward마다 0으로 초기화. 상태를 이어가고 싶으면 이전 hn을 넘겨도 됨.
        batch_size = x.size(0)
        h0 = torch.zeros(self.layer_dim, batch_size, self.hidden_dim, device=x.device) 

        # out: 모든 시점의 은닉 상태 (batch, seq_len, hidden_dim)
        # hn : 각 층의 마지막 시점 은닉 상태 (num_layers, batch, hidden_dim)
        out, hn = self.rnn(x, h0)

        # many-to-one: 마지막 시점의 은닉 상태만 뽑아옴 (many-to-one 구조)
        last_hidden = out[:, -1, :]       # (batch, hidden_dim)

        # 마지막 은닉 상태 → 선형층 → 최종 예측 결과 (예: 클래스 확률 전 단계 값)
        logits = self.fc(last_hidden)     # (batch, output_dim)
        return logits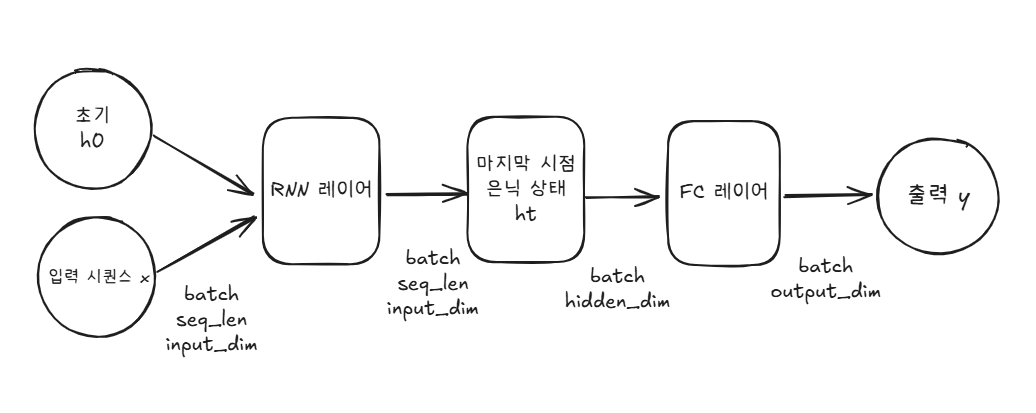

정리하며

RNN은 시퀀스를 처리하기 위한 기본적인 순환 구조로, 입력을 따라가며 은닉 상태를 갱신하고 마지막 은닉 상태를 통해 최종 출력을 만들어낸다. 하지만 은닉 상태를 반복적으로 곱해가며 전달하는 과정에서 그래디언트 소실이나 폭발이 일어나, 긴 시퀀스의 정보를 효과적으로 학습하지 못한다는 한계가 있다.