한 주 동안 열심히 레드-블랙 트리를 구현했다. 구현은 했는데 정작 이 자료구조가 어디서 어떻게 쓰이는지는 모르고 있는 것 같아서 한번 공부해보았다.

이진 (탐색) 트리

일단 이진 트리는 정렬되어 있는 자료를 저장할 때 유용하다. 이분 탐색을 시각적으로 구현했다고 볼 수 있기 때문에 탐색, 삽입, 삭제 속도가 빠르다. 또 순회 방향에 따라 내가 원하는대로 자료에 접근할 수도 있다. 하지만 그냥 이진트리의 경우 계속 큰값(혹은 작은값)을 넣어줬을때 한쪽으로 기울고 사실상 배열과 다름없는 자료구조가 되버린다.

그래서 이렇게 균형이 깨졌을 때 회전을 통해 균형을 맞춰주는 균형 트리가 나오게 되었다.

균형 트리

종류

1. AVL 트리
2. 레드 블랙 트리
3. B트리
4. 2-3(-4) 트리

이렇게 다양한 종류의 균형 이진 트리가 나오게 되었다. AVL 트리는 삭제할 때 시간복잡도가 O(logN)을 보장하지 못하기 때문에 논외로 하고 남은 것들 중에 레드-블랙 트리가 상대적으로 규칙이 단순해 많이 쓰이고 있다.

쓰이는 곳

균형 이진 트리

일단 순서가 있는 자료구조를 구현할 때 많이 쓴다고 보면 된다. 삽입과 삭제, 탐색시간 모두 최악의 경우에도 log(N)을 보장되기 때문에 장점이 많다. 물론 순서가 없으면 그냥 해시함수를 이용하면 되서 이경우는 필요가 없다..!

C++

• std::set

• std::map

  자바랑 살짝 다른게 자바는 기본set이 해시셋이라 순서를 보장하지 않는데, c++의 set은 레드블랙트리로 구현되어 있어서 순서를 보장한다. 순서를 보장하지 않는 set은 따로 std::unordered_set 이렇게 있다고 한다.

파이썬

• SortedSet

자바

• TreeSet
• TreeMap
  

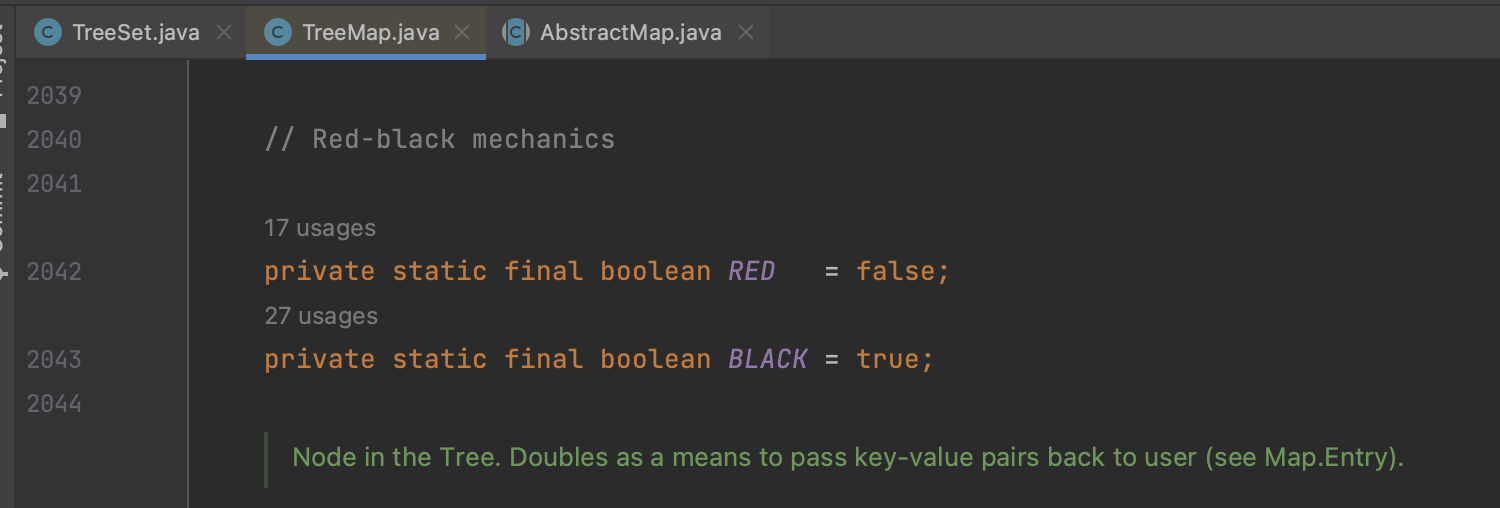
자바의 TreeMap이라는 클래스 내용의 일부를 긁어왔다. 레드와 블랙 상수도 정의 해줬고 익숙한 left_rotate()와 right_rotate()도 있는 걸 보면 레드블랙트리로 이루어져있는 것을 확인할 수 있다.

B트리

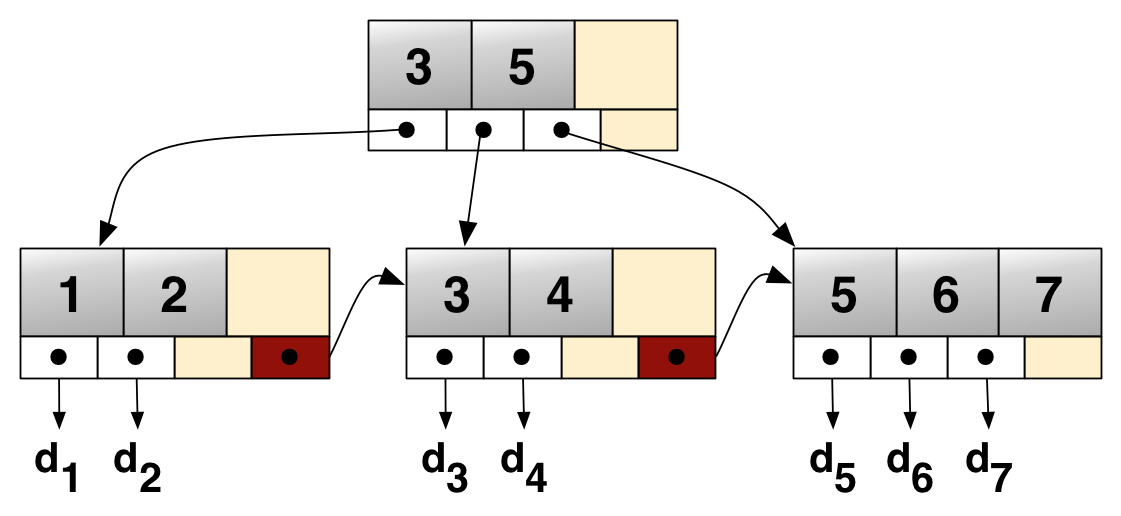
사진은 b+트리

DB 인덱싱을 위한 자료구조로 많이 사용된다. DB에서 쿼리 성능을 향상시키기 위해 인덱스를 만드는데 그 때 해시함수가 아니라 B+트리를 이용해서 만든다고 한다. 해시함수는 범위 검색에 약해서 잘 안쓴다. 레드블랙트리 역시 같은 이유로 잘 쓰이지 않고 대신 B+트리를 주로 쓴다고 한다.

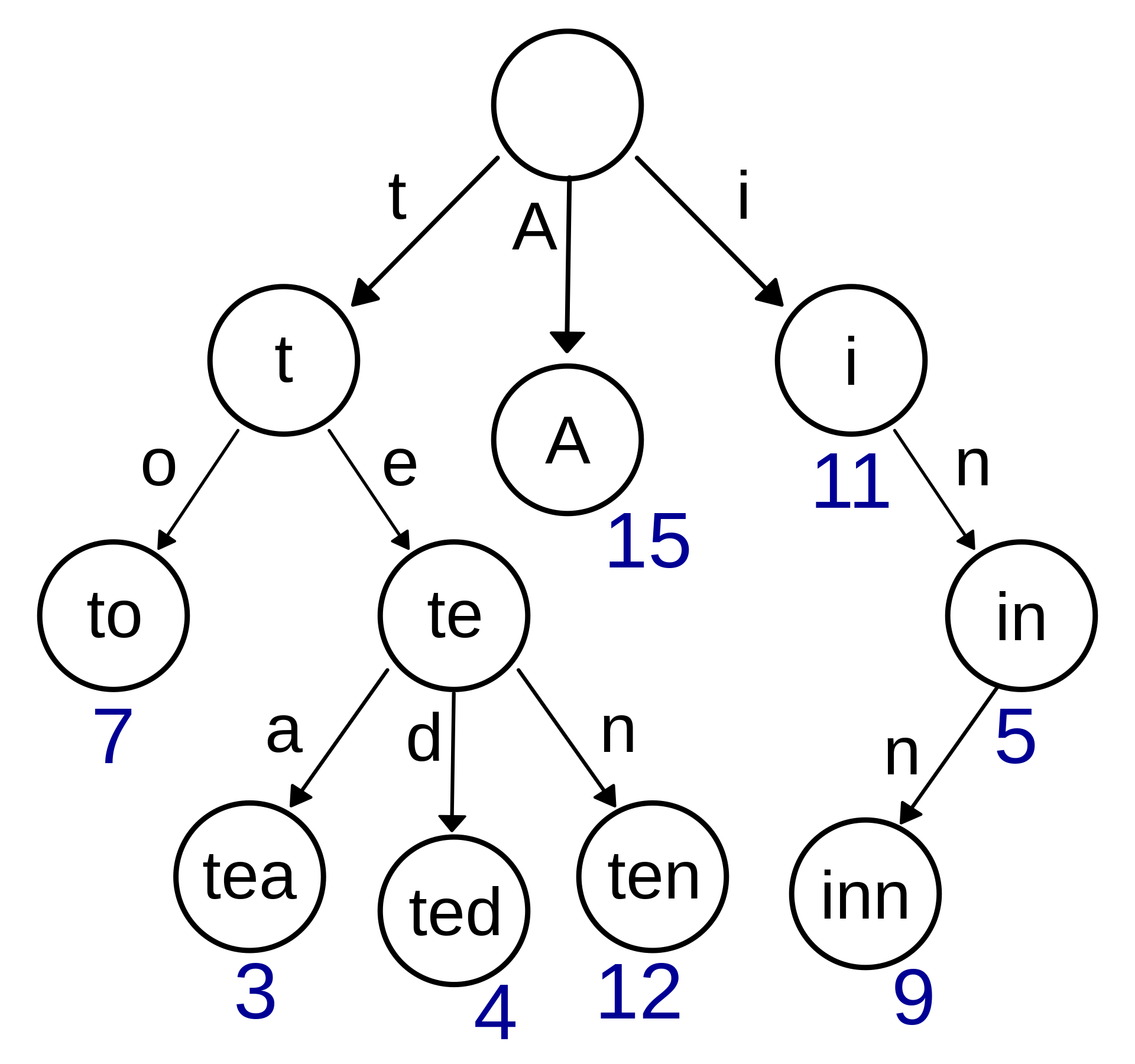
번외 (트라이)

트리 형태의 자료구조 중 트라이(Trie)라고 있는데 얘는 문자열 저장에 특화된 트리이다. 검색어 자동 완성, 문자열 검사, 사전 찾기 에 쓰인다. 균형트리는 아님!