문제

https://www.acmicpc.net/problem/2579

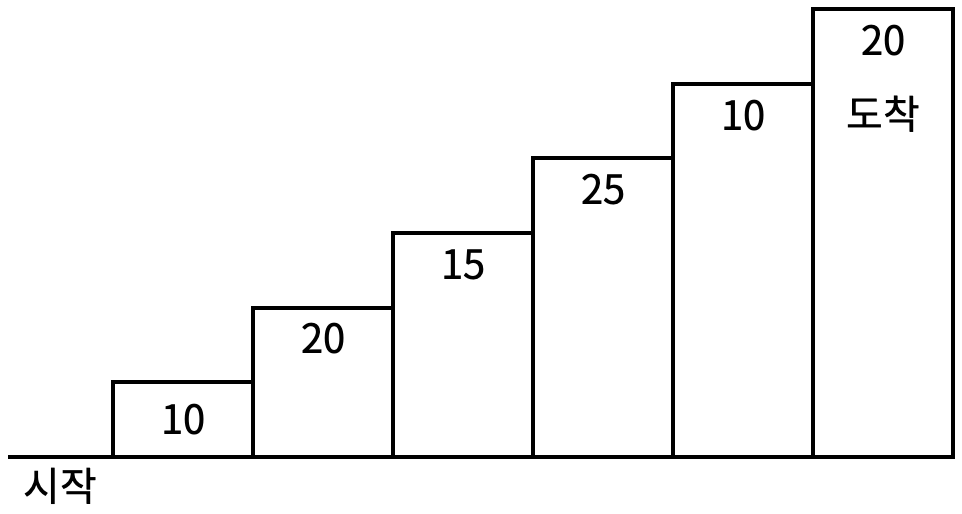
위와같은 계단이 있을때 시작 ~ 도착까지 계단을 밟고갈때 가장 높은 점수를 얻는 방법을 찾는문제다.
단, 조건이 있는데 계단은 연속으로 2회를 밟지 못한다.
이때 시작지점은 계단에 포함되지 않으며, 도착지점은 반드시 밟아야 한다.

입력

• 첫째줄: 계단의 개수
  • 300 이하의 자연수
• 2째줄 ~ 마지막: 계단에 쓰여진 점수
  • 10,000 이하의 자연수

출력

• 얻을 수 있는 총 점수의 최댓값

정답코드

const stdin = require('fs').readFileSync(0, 'utf-8');
const input = (() => {
  let line = 0;
  return () => +stdin[line++];
})();

function solution(N, stairs) {
  const dp = [
    stairs[0],
    stairs[0] + stairs[1],
    Math.max(stairs[0], stairs[1]) + stairs[2],
  ];

  for (let i = 3; i < stairs.length; i++) {
    const a = dp[i - 3] + stairs[i - 1] + stairs[i];
    const b = dp[i - 2] + stairs[i];
    dp[i] = Math.max(a, b);
  }

  if (N === 1) return stairs[0];
  if (N === 2) return stairs[0] + stairs[1];
  return dp.at(-1);
}

const N = input();
const stairs = Array.from({ length: N }, () => input());
const result = solution(N, stairs);
console.log(result);

코드설명

dp 문제는 맨 마지막에서 어떤식으로 가야할지 본다면 쉽게 풀린다.
계단오르기 문제의 경우 맨 마지막 계단에서 본다면 두가지 경우로 마지막 계단에 도달할수 있다.
왜냐하면 계단을 연속으로 2칸으로 뛰지 못하기 때문이다.

1칸 이전에서 오는경우, 2칸 이전에서 오는경우가 있다.
2칸 이전은 간단하게 2칸 이전의 dp + 현재칸의 점수를 더하면 되는데

1칸 이전의 경우 조건을 하나 추가해 주지 않으면 모든칸을 연속으로 밟을수도 있게된다.
3칸 이전의 dp + 1칸 이전의 점수 + 현재칸의 점수를 더해주면
연속으로 2칸까지만 뛸수 있다는 조건을 만족할수 있게 된다.

그래서 최대값은 이 두가지 경우의 수 중 더 큰 값을 dp에 저장하면 된다.
즉, dp[i] = max(dp[i - 3] + stairs[i - 1] + stairs[i], dp[i - 2] + stairs[i])이다

틀렸던 방법

처음이 정답에 거의 근접했는데 틀렸다.
아래처럼 풀었기 떄문이다 ㅠㅠㅠ

for (let i = 3; i < stairs.length; i++) {
  const one = dp[i - 1];
  const two = dp[i - 3] + stairs[i - 2];
  dp[i] = Math.max(one, two);
}

이때 틀린 이유는 두가지다.
1. 현재 dp에 이전계단에서 현재 계단으로 왔을때의 최댓값을 저장해줬다.
2. 그리고 3칸 이전의 dp + 2칸 이전의 계단을 더해줬다.

1은 마지막에 stairs[i]를 더해주면 해결된다.
2는 dp[-3] + 계단[-2], dp[-1]을 비교했는데 이게 아니라
dp[-3] + 계단[-1], dp[-2]를 비교해줬어야 했었다.

이런식으로 풀었던 이유는 전에 풀었던 명량한 아리의 외출 문제를 풀고 이를 너무 의식한것같다.
이때는 마지막엔 아무것도 하지 않기때문에 dp에 이를 저장하지 않고, 이 전의 값들로만 비교했다.
그런데 이 문제는 현재 계단을 밟는다 라는 조건이 있기때문에 이를 추가해줬어야 했다.

앞으로 dp문제를 풀때는 주어진 조건을 잘 보고 이해하자!