문제

https://www.acmicpc.net/problem/25170

시작위치 -> 종료위치를 가야할 때 주어진 시간안에 일을 가장 많이 할 수있는 방법을 찾는 문제다.

입력

• 1행: N, M, T
  • 보드의 세로크기: $2\leq N$
  • 보드의 가로크기: $M \leq 50$
  • 남은 시간: $N + M - 1 \leq T \leq 500$
• 2행 ~ 2 + M - 1 행: w(i, j) 장소에서 할 수 있는 일들의 개수, 정수 $w_ij$
  • $0 \leq w_ij \leq 100$
• 2 + M 행 ~ 2 + M*2 -1행: w(i, j) 장소에서 일을 했을때 걸리는 시간, 정수 $t_ij$
  • $0 \leq t_ij \leq 100$
• 단, 시작부분과 끝부분에서 할수있는 일은 존재하지 않는다.

출력

• 출발지에서 도착지까지 제한시간내에 갈 떄 시간내에 할수있는 일의 최대치

정답코드

const stdin = require("fs").readFileSync(0, "utf-8")
  .trim()
  .split("\n");
const input = (() => {
  let line = 0;
  return () => stdin[line++].split(" ").map(Number);
})();

const [N, M, T] = input();
const direction = [
  [-1, -1], //대각선
  [-1, 0], //위
  [0, -1], //왼쪽
];
// 보드 바깥을 벗어나지 않는지 확인하는 함수
const isInBoard = (y, x) => {
  if (y >= 0 && y < N && x >= 0 && x < M) return true;
  return false;
};
const board = Array.from({ length: N }, () =>
  Array.from({ length: M }, () => [])
);
const dp = Array.from({ length: N }, () =>
  Array.from({ length: M }, () => Array(T + 1).fill(-1))
);

// 입력부분
for (let y = 0; y < N; y++) {
  for (let x = 0; x < M; x++) {
    // 첫칸은 거름
    if (y == 0 && x === 0) continue;

    for (let t = 1; t <= T; t++) {
      // 왼쪽, 대각선, 위방향 탐색
      direction.forEach(([ny, nx]) => {
        const [py, px] = [y + ny, x + nx];
        // 만약 해당 방향에서 현재 방향으로 올 수 있다면
        if (isInBoard(py, px)) {
          const beforeDp = dp[py][px];
          const [beforeWork, beforeTime] = board[py][px];
          const calcTime = t - 1 - beforeTime;

          dp[y][x][t] = Math.max(
            // 현재 dp
            dp[y][x][t],
            // 일을 안할경우
            beforeDp[t - 1],
            // 일은 한경우
            calcTime >= 0 && beforeDp[calcTime] !== -1
              ? beforeDp[calcTime] + beforeWork
              : -1
          );
          dp[y][x][t] = Math.max(dp[y][x][t], beforeDp[t - 1]);
        }
      }); // 왼쪽, 대각선, 위방향 탐색 forEach 종료
    } // T 탐색 종료
  } // x 종료
} // y 종료

const result = Math.max(...dp[N - 1][M - 1]);
console.log(result);

코드 설명

코드에서 중요한 부분만 설명을 해도 될것같다.

const direction = [
  [-1, -1], //대각선
  [-1, 0], //위
  [0, -1], //왼쪽
];

...

// 왼쪽, 대각선, 위방향 탐색
direction.forEach(([ny, nx]) => { ... }

위 코드는 중복되는 부분이 세개 있어서 넣었는데 다른 방법으로 풀어도 상관없다.
그저 대각선, 왼쪽, 위 방향을 확인하기 위해 넣은 부분이다.

// py = y + ny, px = x + nx
const [py, px] = [y + ny, x + nx];
// 만약 해당 방향에서 현재 방향으로 올 수 있다면
if (isInBoard(py, px)) {
  // beforeDp = 이전 위치의 dp
  const beforeDp = dp[py][px];
  // [이전위치의 일 개수, 드는 시간] = board[py][px]
  const [beforeWork, beforeTime] = board[py][px];
  const calcTime = t - 1 - beforeTime;
  
  dp[y][x][t] = Math.max(
    // 현재 dp
    dp[y][x][t],
    // 일을 안할경우
    beforeDp[t - 1],
    // 일은 한경우
    calcTime >= 0 && beforeDp[calcTime] !== -1
    ? beforeDp[calcTime] + beforeWork
    : -1
  );
}

이 부분이 코드의 핵심부분이다.
dp[y][x][t]에서 최대값을 찾기 위해선 세가지 방향에서 올때 일을 하고올때, 안하고 올때를 구분지어서 최대값을 찾아줘야 하는데 해당 부분에 대한 코드이다.

우선 일을 안하고 올 경우에는 간단하다.
그저 현재 dp[y][x][t]와 dp[y][x][t-1]중 최대값을 찾아주면 된다.
t-1을 하는 이유를 모르겠다면 아래에서 자세히 설명하도록 하겠다.

만약 이전 위치에서 일을 하고 올 경우에는 두가지 경우를 더 생각해야한다.
calcTime은 t - 1 - (일했을때 소요된 시간) 이다. 이것역시 아래에서 자세히 설명할것이다.
calcTime이 0 미만이면 비교할 수 없기 때문에 비교하지 않고,
dp[y][x][t] == -1 이라면 해당 t에는 절대 해당 위치에 도달할 수 없기때문에 비교하지 않는다.
그래서 두가지 경우가 아닌경우 dp[y][x][t-1-(소요시간)] + 이전칸에서 소요시간과 현재 dp[y][x][t]를 비교한다.

try1

문제를 보자마자 이 문제는 dp로 풀어야겠다고 생각했다.
하지만 dp[y][x]에 어떠한 값을 저장해야 하는지 감이 안왔다.

이 문제에서 고민해 봐야 할건 대각선 방향에서, 왼쪽 방향에서, 위 방향에서 현재 위치로 왔을때
최대한 많은 일을 하되, 적은 시간을 사용한 값을 dp[y][x]에 어떻게 저장할까? 하는 것이다.

처음엔 dp[y][x]에 이전 위치에서 일을 했을때 안했을때에 대한 경우를 저장하려 했지만
이렇게 한다면 가중치를 줘서 해당 값을 줘야 했었다.

대각선에서 일을 하고올때, 대각선에서 일을 안하고 올때
왼쪽에서 일을 하고올떄, 왼쪽에서 일을 안하고 올때
위에서 일을 하고올때, 위에서 일을 안하고 올때

위의 6가지 경우들에서 (시간 / 한일)에 대한 가중치중 가장 큰 값을 dp[y][x]에 저장하는 방법이다.
하지만 이 방법은 틀릴수밖에 없었다. 가중치가 같을 경우를 처리해 준다고 해도 dp에 시간에 대한 정보가 없기때문에 마지막 칸에 도달했을때 정답이 맞는 경우도 있겠지만 틀린 경우도 존재한다.

try2

그래서 두번째 시도부터 dp[y][x]에 시간들에 대한 정보를 저장 해주게 됐다.
그냥 dp[y][x]에 최대값을 넣어주려 했지만 그냥 모든 시간에 대한 정보를 넣어주면 됐었다.

• dp[y][x][t]는 dp[y][x]에 t 시간을 소요해서 갔을때 할수있는 일의 개수다.
• dp[y][x][t-1]은 이전 위치에서 일을 안하고 현재 위치로 이동만 했을때 한 일의 개수다.
• dp[y][x][t-1-(이전위치 소요시간)]+이전위치 일 개수은 이전 위치에서 일을 하고 현재 위치로 이동할 떄 한 일의 개수다.

위에서 t-1을 해주는 이유는 한칸을 이동 할때마다 1의 시간이 소요되기 때문이다.
마찬가지로 t-1-(이전위치 소요시간)을 해준 이유는 1의 시간이 소요된거에 더해 이전에 일을하면 소요되는 시간을 빼준다.

이렇게만 설명하면 아마 이해가 안될지도 모른다.내가 그랬기 떄문이다.
하지만 동작하는 순서를 보면 바로 이해가 될거라 생각한다.

동작순서

동작하는 순서를 볼때는 아래의 그림을 사용하도록 하겠다.
각 칸의 왼쪽값은 해당 칸에서 (일의 개수, 소요시간) 이다.
예를들어 (2,1) 이라면 2개의 일을 완료하면 1의 시간이 소요된다는 뜻이다.

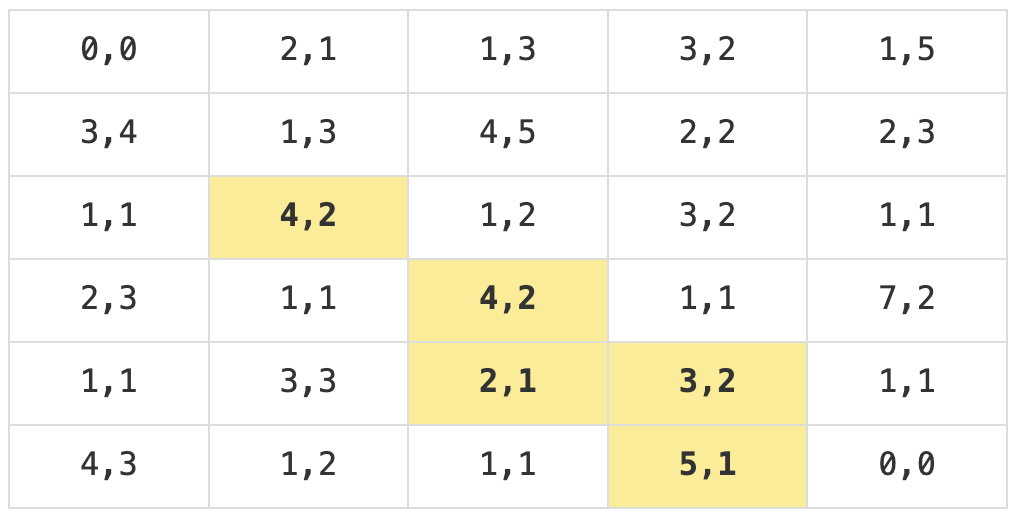
• 위의 그림에서 N=6, M=5, T=15이다.

우선 dp의 모든 값을 -1로 초기화 해주고, dp[0][0][0]=0 으로 초기화 해준다.
그러지 않으면 dp[0][1]에서 탐색을 할때 모든값이 -1이라 제대로 작동하질 않는다.

dp[0][1]부터 탐색을 시작하고, T가 15라서 t는 1~15까지 봐주면 된다.
올수있는 방향은 왼쪽밖에 없으니 dp[y][x-1]만 확인을 하면 된다.
dp[y][x-1]를 beforeDp라 하겠다.

dp[0][0] = [0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1]

---

참고로 앞으로 max에서 비교하는 값은 이렇다

일 안하고 올경우: dp[y][x-1][t-1]
일 하고 올경우: dp[y][x-1][t-1-이전위치 소요시간] + 이전위치 일 개수
현재 위치: dp[y][x][t]

---

이전위치(0,0) 일 개수: 0
이전위치(0,0) 일 했을떄 소요시간: 0

t = 1: dp[0][1][1] = max(dp[0][0][0], dp[0][0][0] + 0, dp[0][1][1]) = max(0,0,-1) = 0
t = 2: dp[0][1][2] = max(dp[0][0][1], dp[0][0][1] + 0, dp[0][1][2]) = max(-1, -1, -1) = -1
...

dp[0][1] = [-1, 0, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1]

---

이전위치(0,1) 일 개수: 2
이전위치(0,1) 일 했을때 소요시간 1

이제 dp[0][2]를 탐색한다. 이때도 왼쪽만 보면 된다.

t = 1: dp[0][2][1] = max(dp[0][1][0], dp[0][1][-1] + 2, dp[0][2][1]) = max(-1,-1,-1) = -1

• 여기서 dp[0][1][-1]은 존재하지 않기 때문에 -1을 대신 넣어 비교한다.

t = 2: dp[0][2][2] = max(dp[0][1][1], dp[0][1][0] + 2, dp[0][2][2]) = max(0, -1, -1) = 0

• 여기서 dp[0][1][0]의 값이 -1 이기 때문에 비교하지 않는다.
• 왜냐하면 dp[y][x][t] == -1 이라면 해당 t에는 이전위치에 도달할수 없기 때문이다.
• 그래서 원래 값 대신 -1을 넣어 비교한다.
  t = 3: dp[0][2][3] = max(dp[0][1][2], dp[0][1][1] + 2, dp[0][2][3]) = max(-1, 2, -1) = 2

...

dp[0][2] = [-1, -1, 0, 2, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1]

---

이전위치(0,2) 일 개수: 1
이전위치(0,2) 일 했을때 소요시간 3

...
t = 3: dp[0][3][3] = max(dp[0][2][2], dp[0][2][0] + 2, dp[0][2][3]) = max(0, -1, -1) = 0

• dp[0][2][0] = -1이기 떄문에 비교하지 않아서 -1로 치환

t = 4: dp[0][3][4] = max(dp[0][2][3], dp[0][2][1] + 1, dp[0][2][4]) = max(2, 1, -1) = 2
...
t = 6: dp[0][3][6] = max(dp[0][2][5], dp[0][2][2] + 1, dp[0][2][6]) = max(-1, 1, -1) = 1
t = 7: dp[0][3][7] = max(dp[0][2][6], dp[0][2][3] + 1, dp[0][2][7]) = max(-1, 3, -1) = 3

dp[0][3] = [-1, -1, -1, 0, 2, -1, 1, 3, -1, -1, -1, -1, -1, -1, -1, -1]

---

이 이후로도 위와 동일한 알고리즘으로 동작한다.
그러고서 마지막에 Math.max(...dp[N-1][M-1])의 값을 출력하면
결과가 나오게된다.