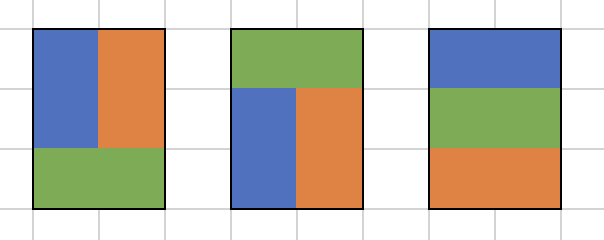
타일링 시리즈

• LV1. 11726: 2xn 타일링
• LV2. 11727: 2xn 타일링 2
• LV3. 2133: 타일 채우기
• LV4. 14852: 타일 채우기 3
• LV5. 아방가르드 타일

문제

https://www.acmicpc.net/problem/2133
3×N 크기의 벽을 2×1, 1×2 크기의 타일로 채우는 경우의 수를 구해보자.

풀이

이번 문제는 푸는데 꽤 애를 먹었다.
바로 전에 풀었던백준11726: 2xn 타일링1과 백준117: 2xn 타일링와는 비슷한듯 다른 문제이기 때문이다.
n이 1일때 ~ 4일때 어떤 도형들이 있는지부터 살펴보자.

우선 이 문제의 세로 크기는 3이기때문에 n이 홀수일때는 경우의수가 존재하지 않는다.

1. n = 2

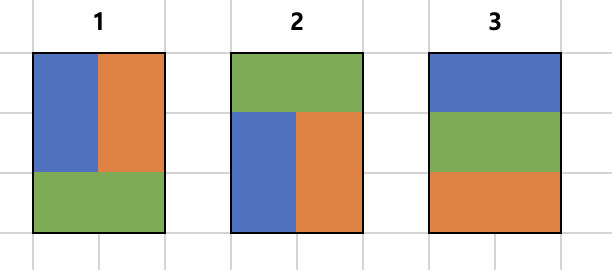
1x2 타일과 2x1의 타일로 만들 수 있는 모든 경우의 수는 위와 같이 3개다.
그리고 앞으로 해당 조합으로 만든 타일 모양을 1, 2, 3 으로 부를것이다.

dp[2] = 3

2. n = 4

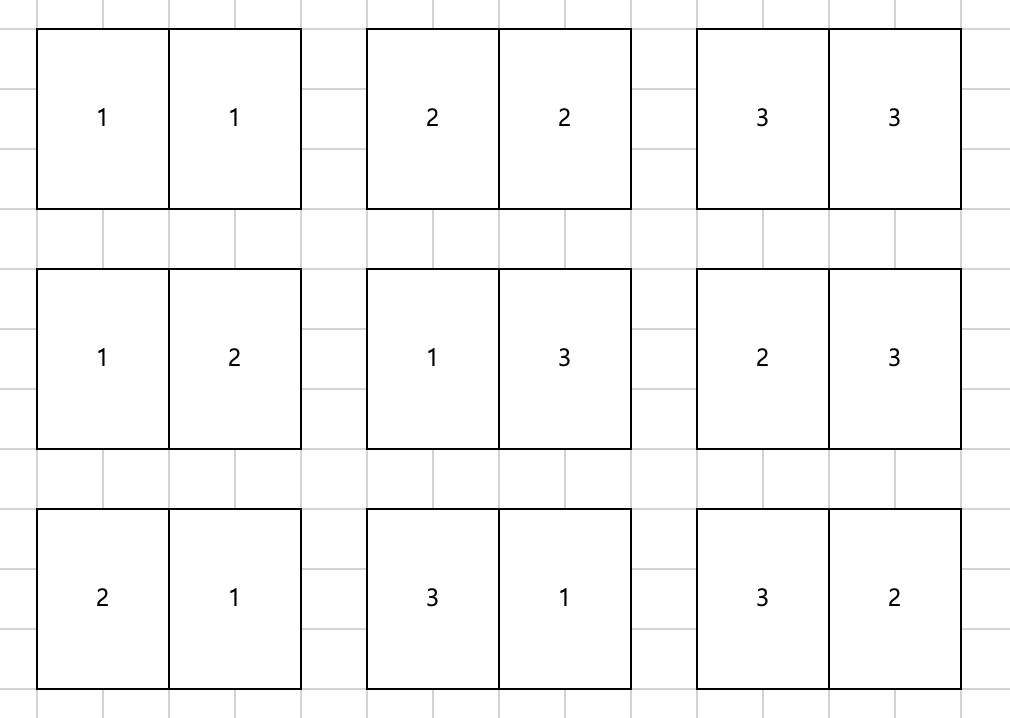
4일때는 n이 2일때의 타일을 앞뒤에 붙여서 혹은 두번 사용해서 모양을 만든다.

근데 여기에 더해 n이 4 이상일때 나오는 유니크 패턴이 존재한다.
이것때문에 문제를 어떻게 풀지 더 헤맸던것같고, 유니크패턴은 아래와 같이 두개다.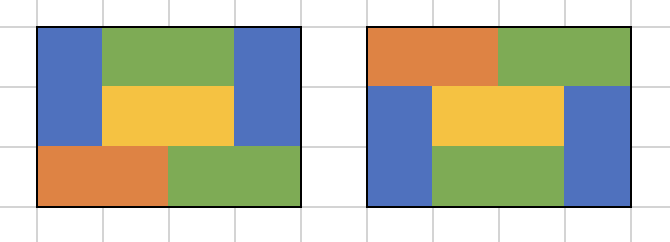

dp[4] = dp[2] * dp[2] + 2 = 9 + 2 = 11

3. n = 6

지금까지의 과정에 따르면 점화식은 이렇게 된다.

dp[n] = dp[n-2] * dp[2] + 2

그러면 dp[6] = dp[4] * 3 + 2 = 33 + 2 = 35 일까?
정답은 절반만 맞다. 왜일까?

위에서 n이 4 이상일때는 유니크 패턴이 존재한다고 했다.
근데 n=6일때 이 경우의 수를 고려하지 않았다.

즉, n=2 일때 도형의 옆에 n=4 일때의 유티크패턴들을 붙일수가 있다는 뜻이다.
그래서 아래의 도형들을 추가해 줘야 한다.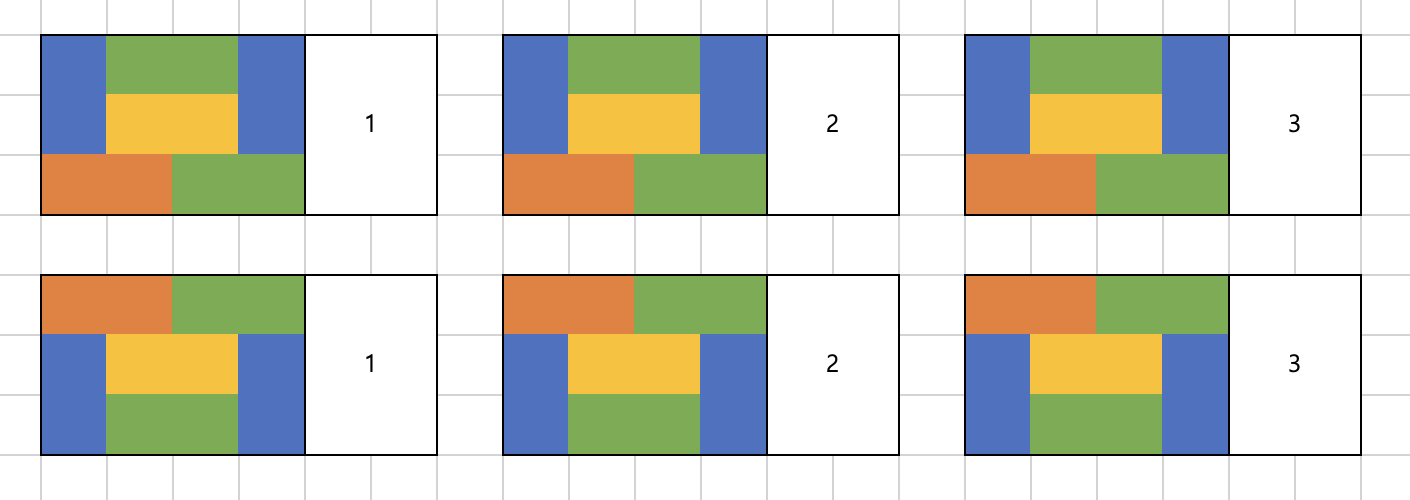

이렇게 n=6일때 답을 구하면 아래와 같이 된다.

dp[6] = dp[4] * dp[2] + dp[2] * 2 + 2 = 33 + 6 + 2 = 41

4. n = 8

n=6일때 n=2 일때 도형의 왼쪽 오른쪽에 n=4 일때의 유니크 패턴을 붙여준다고 했다.

그러므로 n=4일때 도형의 옆에 n=4일때의 유니크 패턴(2개)을 붙여 결과에 더하고
n=2일때 도형의 옆에 n=6일때 유니크 패턴(2개)을 붙여 결과에 더해야 한다.

위의 내용을 모두 정리하면 최종적으로 점화식은 아래와 같은 모양이 된다.

dp[n] = ( dp[n - 2] * dp[2] ) + ( dp[n - 4] * 2 ) + ( dp[n - 6] * 2 ) + ( dp[n - 8] * 2 ) + ... +( dp[0] * 2 ) + 2

dp[8] = ( dp[6] * dp[2] ) + ( dp[4] * 2 ) + ( dp[2] * 2 ) + 2 = 123 + 22 + 6 + 2 = 153

코드

//const stdin = require('fs').readFileSync(0, 'utf-8').trim().split('\n');
const stdin = `30`.trim().split('\n');

const N = +stdin[0];
const dp = Array(31).fill(0);
dp[1] = 0;
dp[2] = 3;

for (let i = 4; i <= N; i += 2) {
  dp[i] = dp[i - 2] * 3 + 2;

  for (let j = i - 4; j >= 0; j -= 2) {
    dp[i] += dp[j] * 2;
  }
}
console.log(dp[N]);