타일링 시리즈

• LV1. 11726: 2xn 타일링
• LV2. 11727: 2xn 타일링 2
• LV3. 2133: 타일 채우기
• LV4. 14852: 타일 채우기 3
• LV5. 아방가르드 타일

문제

https://www.acmicpc.net/problem/14852
2×N 크기의 벽을 2×1, 1×2, 1×1 크기의 타일로 채우는 경우의 수를 구해보자.

이번에도 타일링 문제다.
타일링 문제 유형을 박살내려고 이번주에 타일링 문제만 풀었다.
그리고 이 문제가 처음에 말했던 프로그래머스의 아방가르드 타일링 문제와 매우 흡사하다.
아마 이 문제를 풀었으니 저 문제도 쉽게 풀 수 있을거라 생각된다.

🚨주의사항🚨
1. 정답은 1,000,000,007로 나눈 나머지를 출력해야함
2. n이 100만으로 크므로 시간초과에 주의해서 풀어야함

풀이

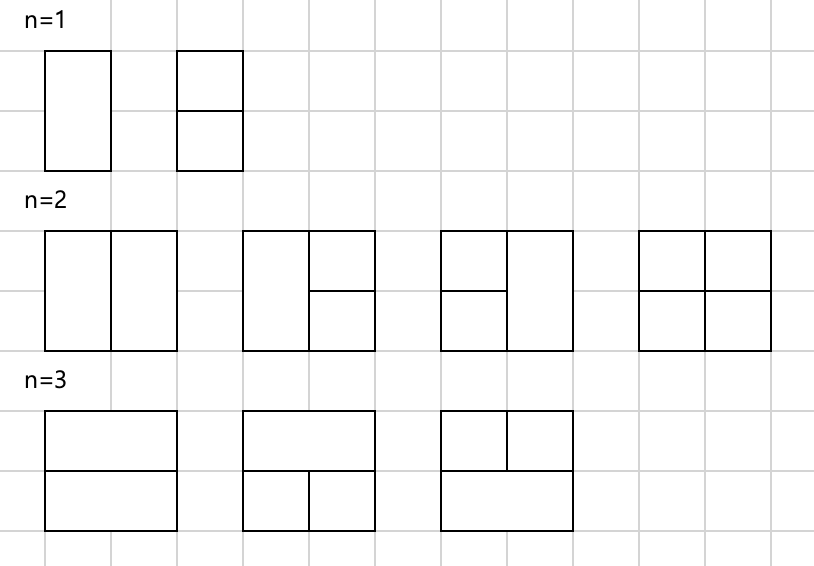
우선 지금까지 타일링 문제를 풀어왔던것처럼 n이 1일때부터 도형들을 나열해서 규칙을 찾아본다.
그리고 세로의 크기가 2이므로 우선 n이 2일때까지만 규칙을 찾아본다.

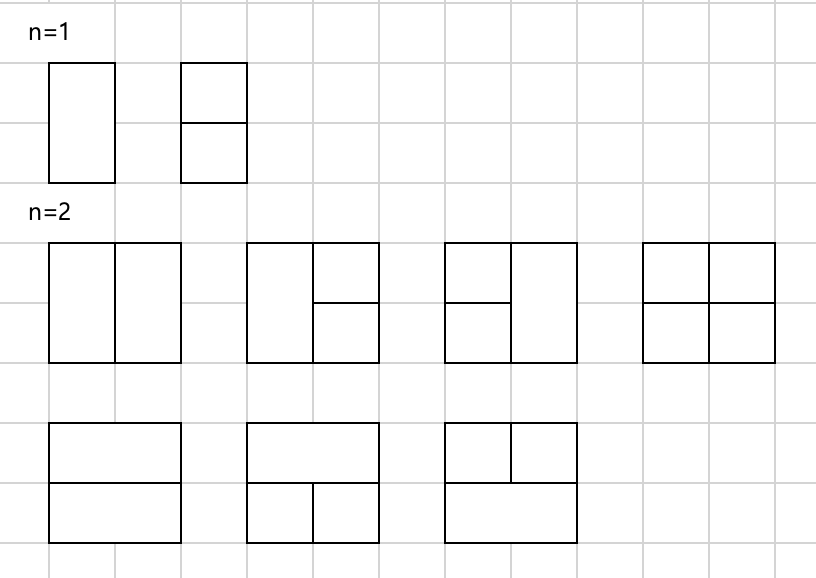
• n이 1일때는 새로 생긴 패턴이 2개고,
• n이 2일때는 새로 생긴 패턴이 가로가 사용된 3개다.

그리고 3, 4, 5, 6일때 유티크 패턴도 찾아본다.

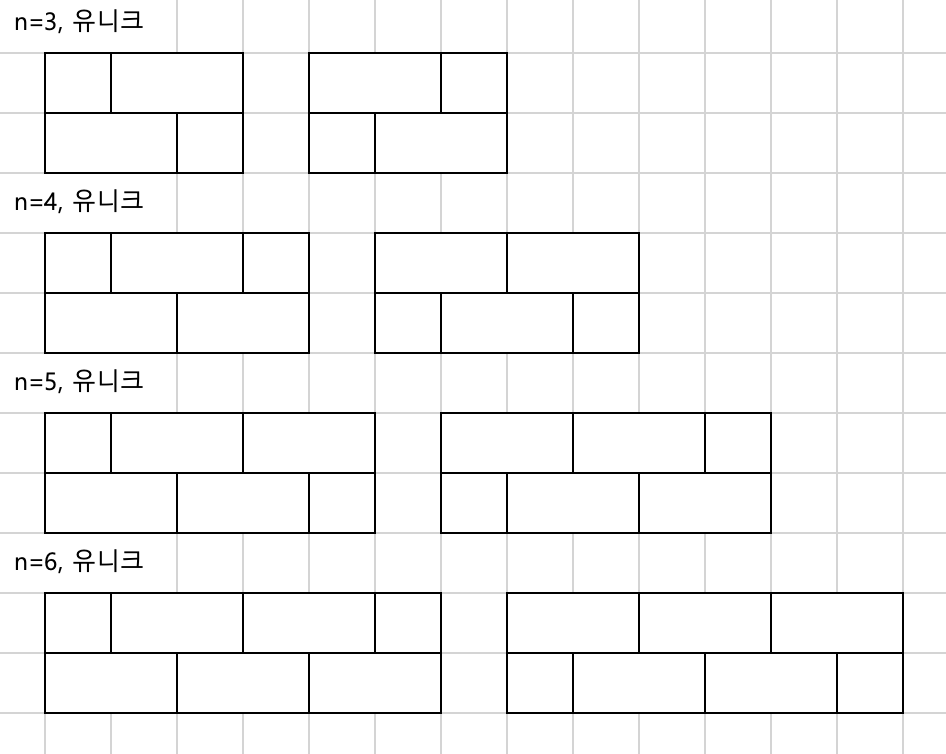
자세히 살펴보면 5, 6일때의 유니크 패턴은 3, 4일때 패턴에 ⎯ 모양 막대기만 추가된 모습을 볼 수있따.
그리고 유티크 패턴은 3 이상일 때 무조건 2개씩 생긴다는것도 알게됐다.

그럼 이제 식을 세워보자 우선 1, 2일때는 아래와 같다.
dp[1] = 1
dp[2] = 7

n = 3

dp[3]
= dp[i-1] * 2 + dp[i-2] * 3 + 2
= 14 + 6 + 2
= 22
dp[3] = 22

dp[i-1]에 2를 곱하는 이유는 n=1일때 새로 생긴 패턴은 두개이기 때문이다.
dp[i-2]에 3을 곱하는 이유도 위와같다.
더 자세한 설명은 이전글 을 읽어보면 자세하게 이해가 될것이다.

n = 4

dp[4]
= dp[i-1] * 2 + dp[i-2] * 3 + dp[i-3] * 2 + 2
= 44 + 21 + 4 + 2
= 71

여기서 dp[i-3]에 2를 곱하는 이유는
n=1일때 오른쪽에 n=3일떄의 유티크 패턴을 붙여 새로운 패턴을 만들어낼 수 있기 때문이다.
여기서 i-3부터 생기는 유니크 패턴은 모두 2개씩 이므로 i-3 이후에는 2를 곱하면 된다는 사실을 알게된다.

n = 5

여기까지 이해했다면 5일때도 구하기 쉽다.
dp[5]
= dp[i-1] * 2 + dp[i-2] * 3 + dp[i-3] * 2 + dp[i-4] * 2 + 2
= 142 + 66 + 14 + 4 + 2
= 228

점화식

dp[i] = ( dp[i-1] * 2 ) + ( dp[i-2] * 3 ) + ( dp[i-3] * 2 ) + ( dp[i-4] * 2 ) + ( dp[i-5] * 2 ) + ... + ( dp[0] * 2 )

dp에서 dp[0]의 값은 사용하지 않으므로 dp[0]을 2로 설정해놓으면 위와같은 점화식이 완성된다.

정답코드?

//const stdin = require('fs').readFileSync(0, 'utf-8').trim().split('\n');
const stdin = `5`.trim().split('\n');
const N = +stdin[0];
const dp = Array(1_000_001).fill(0);
dp[1] = 2;
dp[2] = 7;

for (let i = 3; i <= N; i++) {
  dp[i] = dp[i - 1] * 2 + dp[i - 2] * 3 + 2;
  for (let j = i - 3; j > 0; j--) {
    dp[i] += dp[j] * 2;
  }
}

console.log(dp[N]);

아쉽게도 이 코드는 정답이 아니다.
n이 10만이기에 n^2의 코드로는 통과할 수 없기 때문이다.
그래서 for문을 계속 돌려서 정답을 구해주는 대신
지금까지 곱했던걸 누적합에 저장해놓고 사용하기만 하면 문제는 해결된다.

정말 정답코드

//const stdin = require('fs').readFileSync(0, 'utf-8').trim().split('\n');
const stdin = `5`.trim().split('\n');
const N = +stdin[0];
const dp = Array(1_000_001).fill(0);
const memo = [2, 6, 20];
dp[1] = 2;
dp[2] = 7;

for (let i = 3; i <= N; i++) {
  const calc = dp[i - 1] * 2 + dp[i - 2] * 3 + memo[i - 3];
  dp[i] = calc % 1_000_000_007;
  memo[i] = (memo[i - 1] + dp[i] * 2) % 1_000_000_007;
}

console.log(dp[N]);