타일링 시리즈

• LV1. 11726: 2xn 타일링
• LV2. 11727: 2xn 타일링 2
• LV3. 2133: 타일 채우기
• LV4. 14852: 타일 채우기 3
• LV5. 아방가르드 타일

문제

https://school.programmers.co.kr/learn/courses/30/lessons/181186

정우는 예술적 감각이 뛰어난 타일공입니다. 그는 단순한 타일을 활용하여 불규칙하면서도 화려하게 타일링을 하곤 합니다.
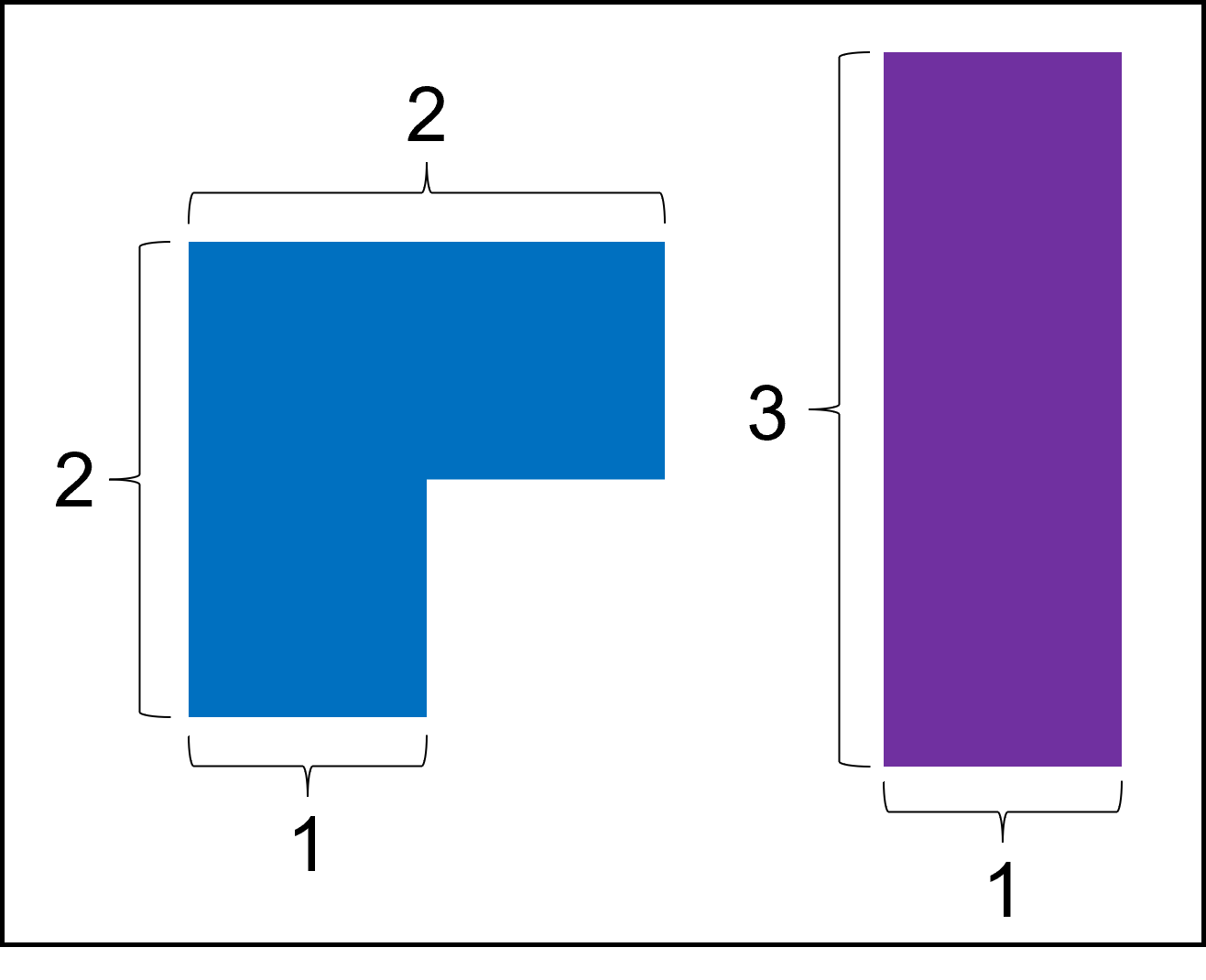
어느 날 정우는 가로 길이 n, 세로 길이 3 인 판을 타일링하는 의뢰를 맡았습니다. 아방가르드한 디자인 영감이 떠오른 정우는 다음과 같은 두 가지 종류의 타일로 타일링을 하기로 결정했습니다.

각 타일은 90도씩 회전할 수 있으며 타일의 개수는 제한이 없습니다.

n이 주어졌을 때, 이 두 가지 종류의 타일로 n x 3 크기의 판을 타일링하는 방법의 수를 return 하도록 solution 함수를 완성해주세요.

이전에 풀었던 문제들과 비슷한 타일링 문제다.
하지만 훨씬 어려웠고, 생각하는데 시간이 오래걸렸따.
만약 타일링 문제를 처음 풀어본다면 이전이전글 에 자세하게 써놨으니 읽어보면 도움이 될거라 생각한다.

풀이 1

n이 1, 2, 3일때 새로 생기는 패턴의 개수는 생각보다 많지 않다.

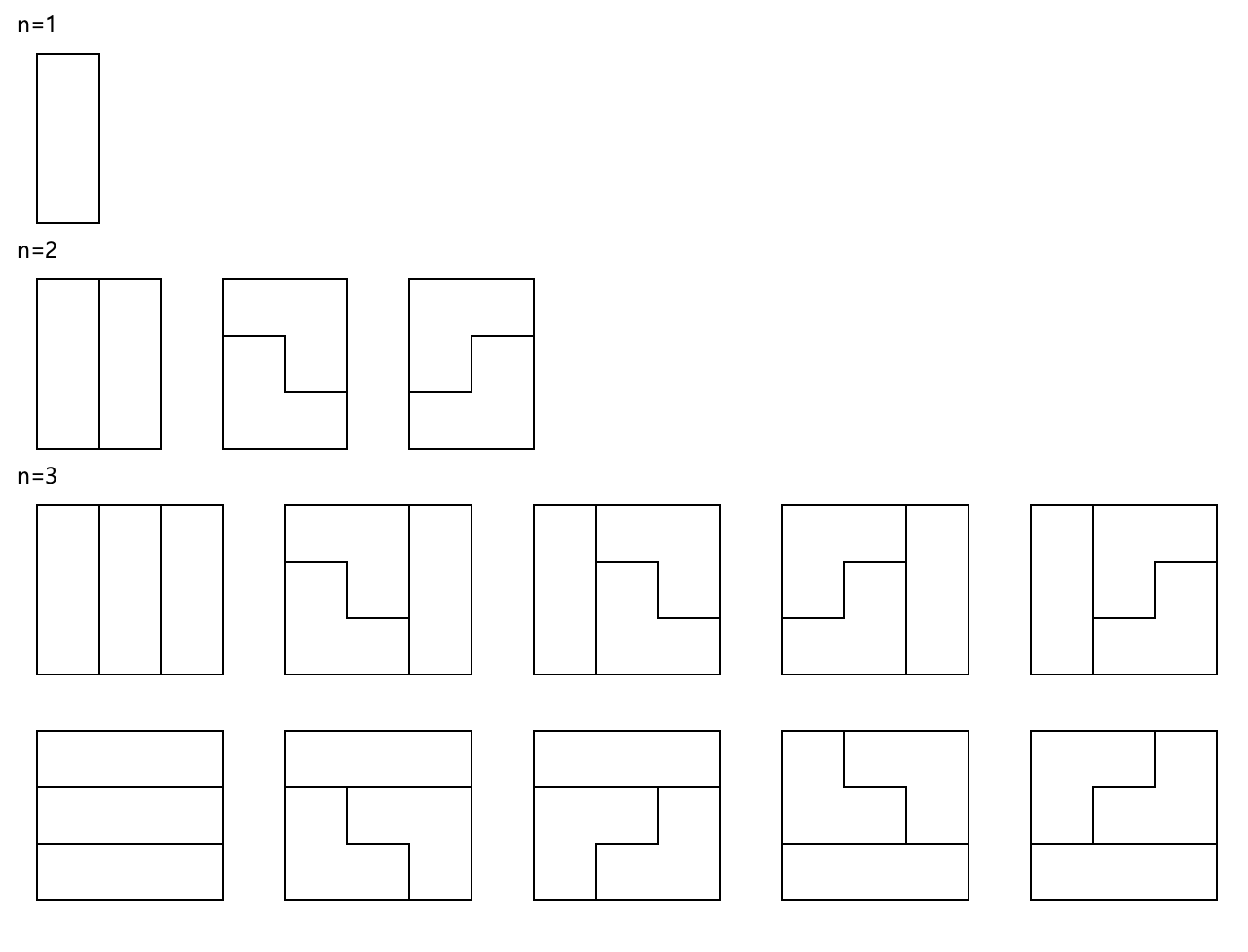
n=1 일때 새로 생긴 패턴 => 1개
n=2 일때 새로 생긴 패턴 => 2개
n=3 일때 새로 생긴 새턴 => 5개

그리고 n이 4, 5, 6일때 유니크 패턴은 아래와 같다.

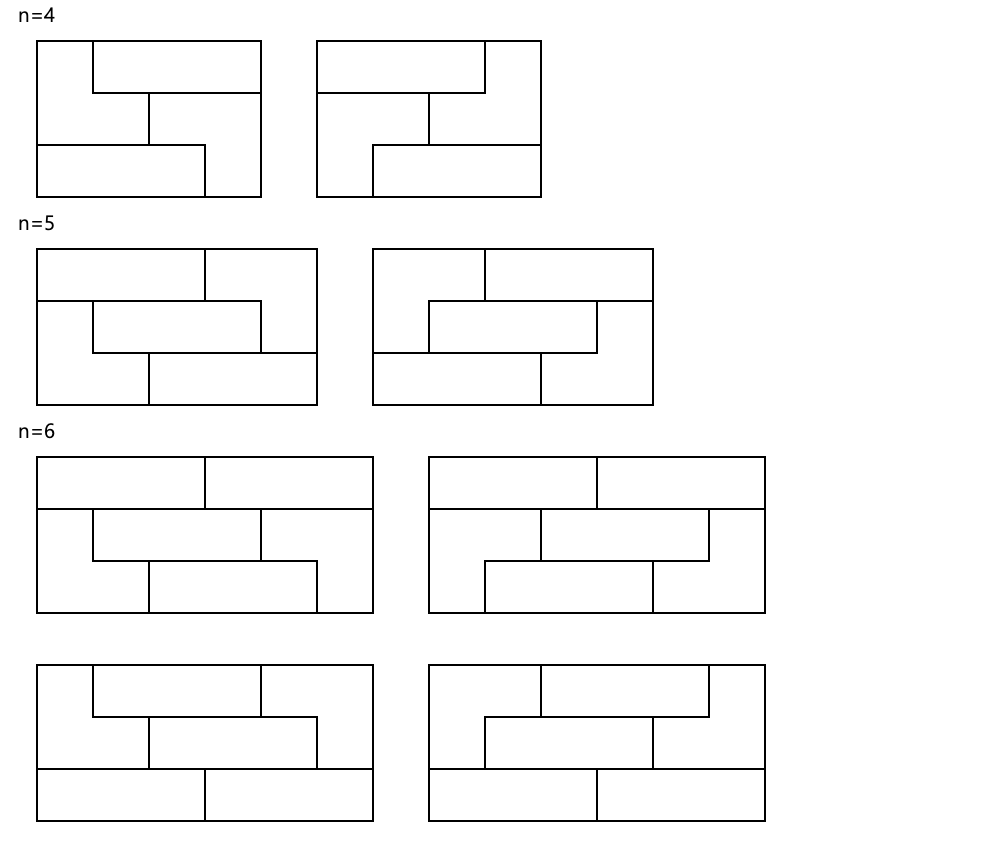
n이 7 이상일때를 그려보면 4, 5, 6일때 패턴이 반복되는것이 보인다.
그래서 4 이후로는 2, 2, 4가 반복된다.

결론은 새로 생기는 패턴은 1, 2, 5, 2, 2, 4, 2, 2, 4, ... 가 된다.
그리고 점화식은 아래와 같이 표현된다.

dp[i] = ( dp[i-1] ) + ( dp[i-2] * 2 ) + ( dp[i-3] * 5 ) + ( dp[i-4] * 2 ) + ( dp[i-5] * 2 ) + ( dp[i-6] * 4 ) + ... (2,2,4 반복을 0까지)
식을 세우기전 초기값은 이렇다.

그렇게 얻어진 0 ~ 4 까지의 dp는 이렇다.
마지막에 해당 n의 유니크 패턴을 곱해줄 것이므로 dp[0] 을 1로 설정해줬다.
dp[0] = 1, dp[1] =1, dp[2] = 3, dp[3] = 10, dp[4] = 23 이다.

풀면서 주의할 점은 이 문제도 n이 10만으로 꽤 크므로 이전 문제 처럼 누적합을 써줘야 한다.
그런데 이전문제는 반복되는 패턴이 2 하나였지만 이번에는 2, 2, 4 가 반복된다.
그래서 누적합도 세개를 따로 따로 더해줘야 한다.

예를들어
4일때는 2 4 2 ... 가 반복되는 누적합을
5일때는 2 2 4 ... 가 반복되는 누적합을
6일때는 4 2 2 ... 가 반복되는 누적합을 더해준다.

해당 순서로 반복되는 누적합을 더해줘야 하는 이유는 바로 위의 점화식을 보면 알 수있는데
i-4부터 2 2 4가 거꾸로 반복되기 때문이다.

위의 규칙대로 누적합을 구해보면 아래와 같다

const dp = [1, 1, 3, 10];
const memo = [
  [2, 6, 12, 32], // 2 4 2 2
  [2, 4, 16, 36], // 2 2 4 2
  [4, 6, 12, 52], // 4 2 2 4
];

각각 (i-1) % 3 일때 더해줘야 하는 누적합을 미리 계산해 놨다.

그렇게 완성된 코드는 아래와 같다.

코드 1

function solution(n) {
  const dp = [1, 1, 3, 10];
  const memo = [
    [2, 6, 12, 32], // 2 4 2 2 4 2 2 4 2 2 4  0
    [2, 4, 16, 36], // 2 2 4 2 2 4 2  1
    [4, 6, 12, 52], // 4 2 2 4 2 2 4  2
  ];

  for (let i = 4; i <= n; i++) {
    const now = (i - 1) % 3;
    const t1 = (now + 1) % 3;
    const t2 = (now + 2) % 3;

    dp[i] = (dp[i - 1] + dp[i - 2] * 2 + dp[i - 3] * 5 + memo[now][i - 4]) % 1000000007;

    memo[now][i] = (memo[now][i - 1] + dp[i] * 4) % 1000000007;
    memo[t1][i] = (memo[t1][i - 1] + dp[i] * 2) % 1000000007;
    memo[t2][i] = (memo[t2][i - 1] + dp[i] * 2) % 1000000007;
  }

  return dp[n] % 1000000007;
}

풀이 2

문제를 풀고나서 다른 사람의 풀이를 살펴보니 수학적으로 접근한 풀이법이 있었다.
위에서 구한 점화식은 이렇다.

dp[i] = dp[i-1] + ( dp[i-2] * 2 ) + ( dp[i-3] * 5 ) + ( dp[i-4] * 2 ) + ( dp[i-5] * 2 ) + ( dp[i-6] * 4 ) + ... (2,2,4 반복을 0까지)

그런데 여기서 계수 2,2,4가 반복되는 부분을 아래와같이 제거해줄 수 있다.

dp[i] = dp[i-1] + ( dp[i-2] * 2 ) + ( dp[i-3] * 5 ) + ( dp[i-4] * 2 ) + ( dp[i-5] * 2 ) + ( dp[i-6] * 4 ) ... 계수 2,2,4 반복

dp[i-3] = dp[i-4] + ( dp[i-5] * 2 ) + ( dp[i-6] * 5 ) + ( dp[i-7] * 2 ) + ( dp[i-8] * 2 ) + ( dp[i-9] * 4 ) ...

dp[i] - dp[i-3] = dp[i-1] + ( dp[i-2] * )2 + ( dp[i-3] * 5 ) +dp[i-4] - dp[i-6]

dp[i] = dp[i-1] + ( dp[i-2] * 2 ) + ( dp[i-3] * 6 ) + dp[i-4] - dp[i-6]

이렇게 dp[i] - dp[i-3] 을 하므로 인해 반복되는 부분을 제거할 수 있게 되었고
점화식도 아래처럼 더 깔끔하게 나왔다.

dp[i] = dp[i-1] + ( dp[i-2] * 2 ) + ( dp[i-3] * 6 ) + dp[i-4] - dp[i-6]

코드 2

function solution(n) {
  const mod = 1000000007;
  const dp = [1, 1, 3, 10, 23, 62];
  for (let i = 6; i <= n; i++) {
    dp[i] = (dp[i - 1] + dp[i - 2] * 2 + dp[i - 3] * 6 + dp[i - 4] - dp[i - 6] + mod) % mod;
  }
  return dp[n];
}

참고로 아래에서 mod를 더해주는 이유는 dp[i-6]을 뺏을 때 음수가 나오는 경우도 존재하기 때문이다.
dp[i] = (dp[i - 1] + dp[i - 2] 2 + dp[i - 3] 6 + dp[i - 4] - dp[i - 6] + mod) % mod;