
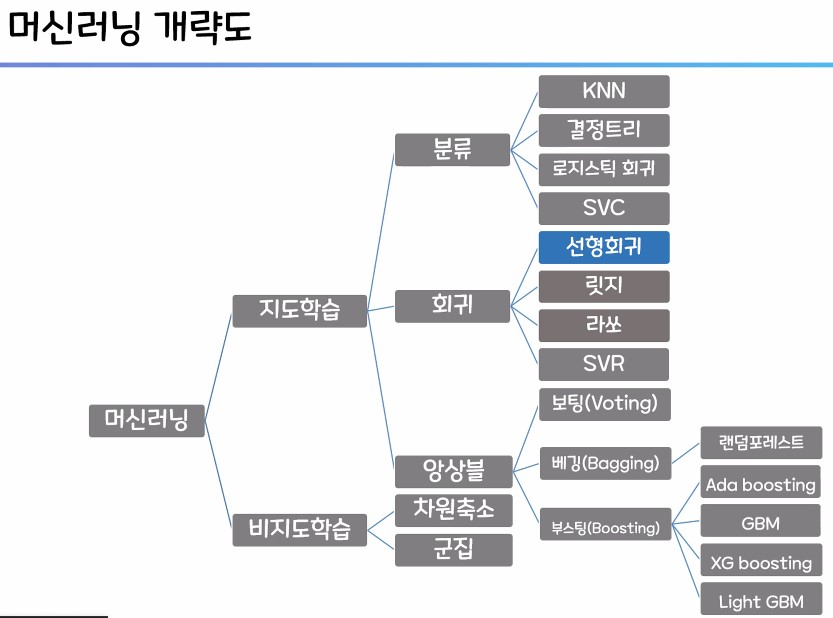
1. 머신러닝의 회귀
- 회귀 및 선현 회귀의 개념과 필요성을 이해 숙지
- 회귀 모델의 평가지표를 이해하고 그 종류를 숙지
- 경사하강법의 개념과
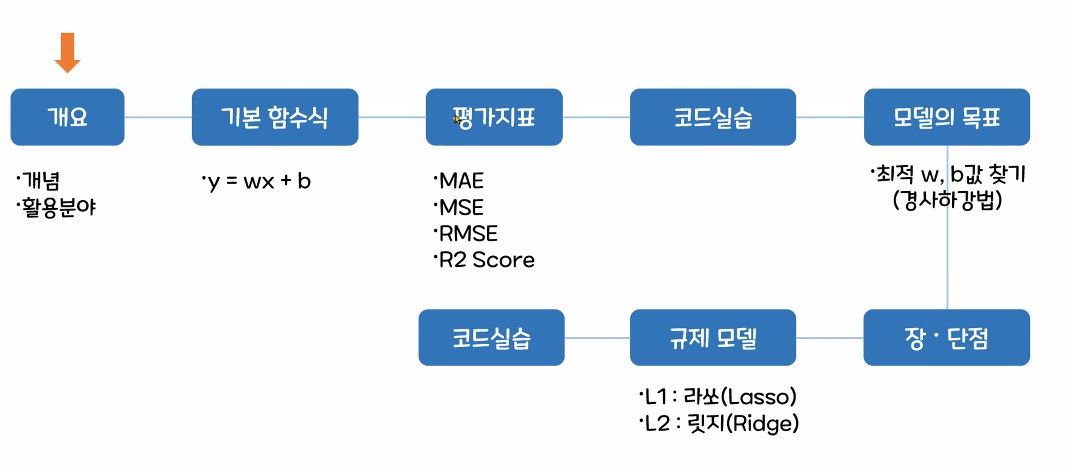
1.1. 선형 회귀 수업 흐름도
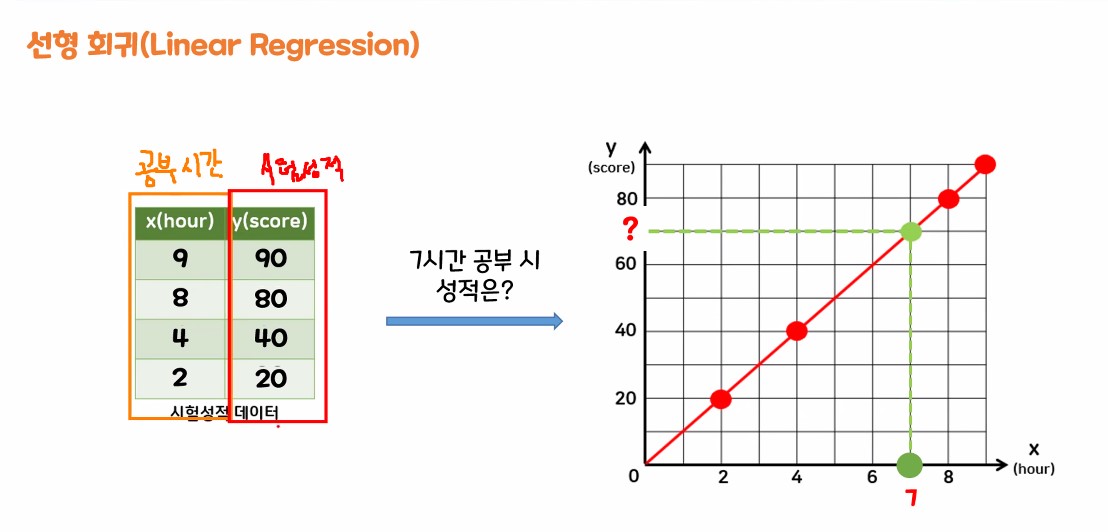
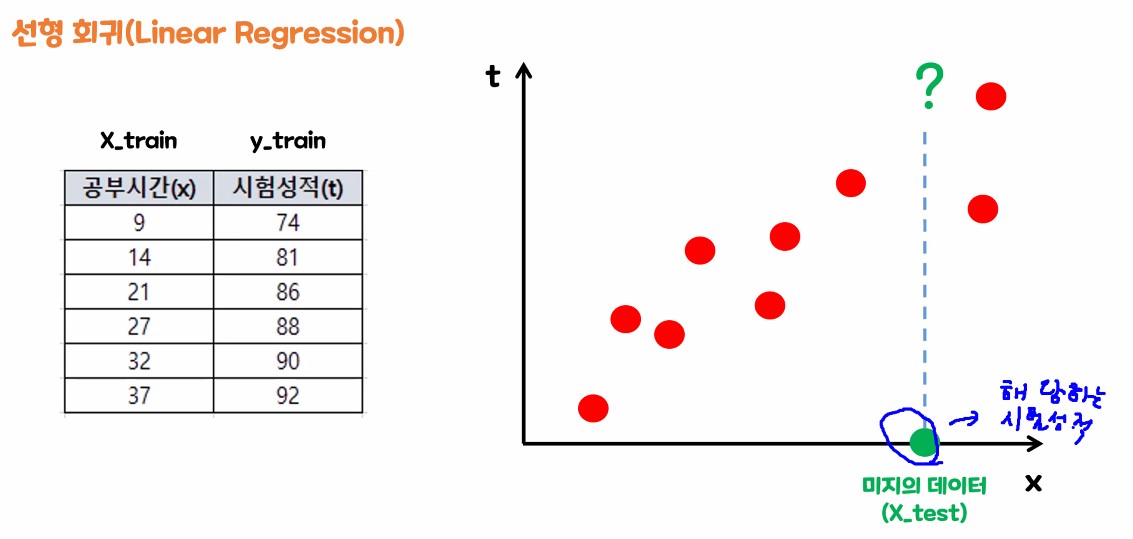
1.2. 선형 회귀(Linear Regression) 란?
- 회귀 : 연속 적인 실수 값을 예측하는 분야
- 선형 회귀 : 직선의 형태를 가지는 1차식으로 연속적인 실수 값을 예측하는 모델
- 여러개의 독립변수 x(특성)와 종속변수 y(예측값)의 선형 상관 관계를 모델링
- 회귀의 중요성 및 필요성

1.3. 선형 회귀
- 수식 y = 10 * x
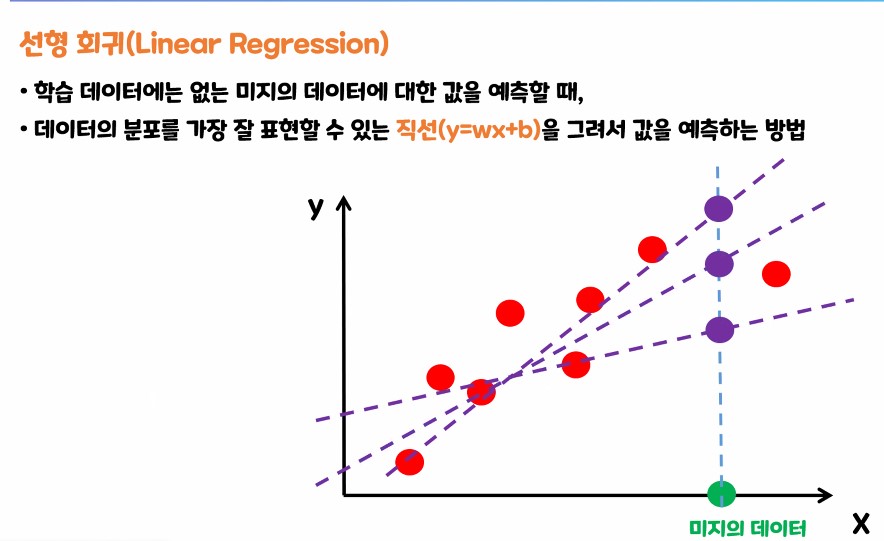
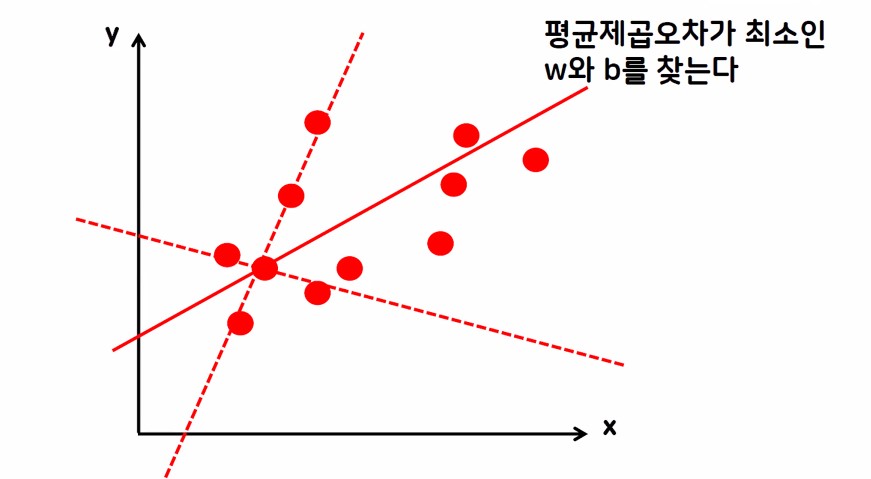
위 3가지 직선 중 어느 선이 잘 예측했는가? => 2번
1.3.1. 1차 함수식

- y : 정답, 예측 값
- =시험성적=예측 값
- x : 문제, 특성 값, 컬럼(특징)
- =공부한 시간=특성 값
- 컴퓨터가 바꿀 수 있는 데이터
- w : 가중치, 특성에 대한 정답 예측 중요도
- b : y축 방향으로 기준 점 위치를 잡아줌
1.3.2. w값 구해보기 (실습)
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# 선형 회귀 모델 import
from sklearn.linear_model import LinearRegression
# 임의에 데이터를 만들어 보자!
X = np.array([[1,2,3,4,5]])
y = np.array([[2,4,6,8,10]])
# 모델 객체 생성
linear = LinearRegression()
# 모델 학습
# 주의점 : 선형 회귀 모델에 들어가는 데이터는 문제와 정답 모두 2차원 이어야 한다!
linear.fit(X,y)
# 선형 그래프를 그리기 위한 1차원 화
X = np.array([1,2,3,4,5])
y = np.array([2,4,6,8,10])
# 그래프를 통해서 직선을 확인 해보자
plt.plot(X, y, marker = 'o')
plt.grid()
plt.show()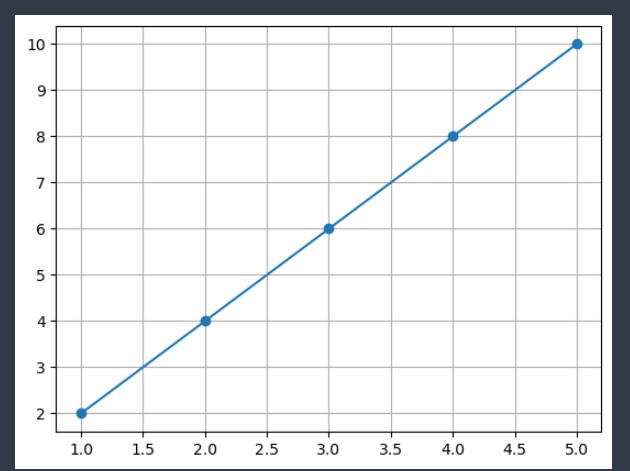
# 가중치 w를 확인하는 방법
print(linear.coef_)
# 편항 b를 확인하는 방법
print(linear.intercept_)
linear.coef_array([[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.]])
1.3.3. 다중 선형 회귀 함수식
- 같은 꽃이지만 여러 종류가 있을 경우, 특성의 분류를 위해 x가 p만큼 늘어남

특성(x)의 개수
- 수식에서 x의 개수
- x의 개수만큼 w의 개수도 늘어남
2. 회귀 모델 평가 지표

2.1. 회귀 모델 평가지표 종류
① MSE
② RMSE

③ MAPE
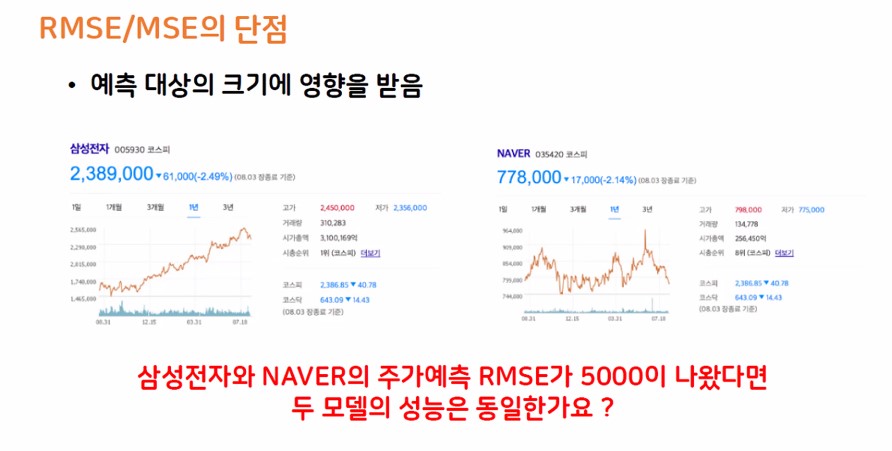
- 2개 이상의 모델을 비교할때 자주사용


- 회귀 함수(직선)가 평균에 비해 얼마나 그 데이터를 잘 설명할 수 있는가에 대한 점수
- 편차 : 예측값과 평균과의 거리
- 오차 : 예측값과 회귀 직선과의 거리
- 일반적으로 0에서 1사이의 값이지만 예측이 심하게 어긋날 경우 -(음수) 값이 나올 수 있음
( -값이 나온다는 것은 회귀 직선이 평균 보다 더 데이터를 잘 설명하지 못한다는 뜻)
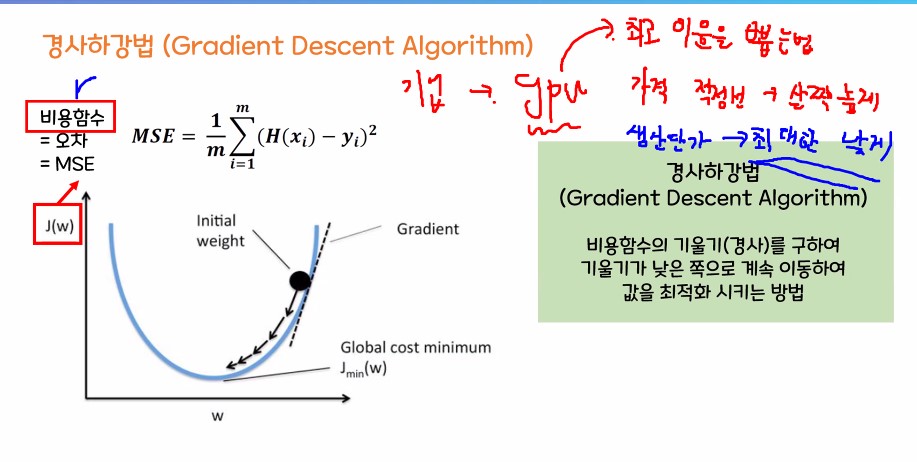
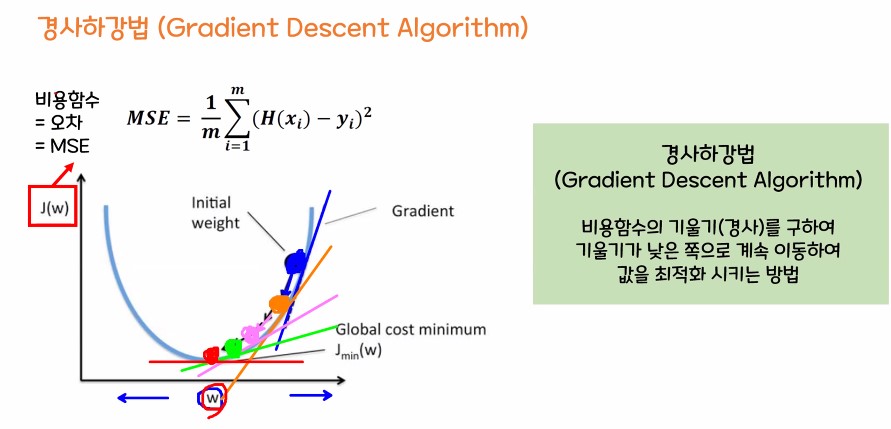
2.2. 회귀 모델의 최종 목표
MSE가 최소가 되는 최적의 w(가중치), b(편항) 값 구하기
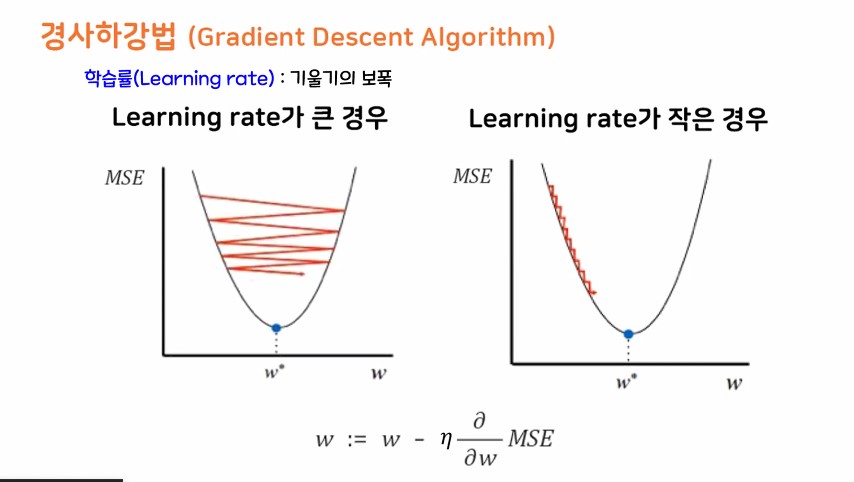
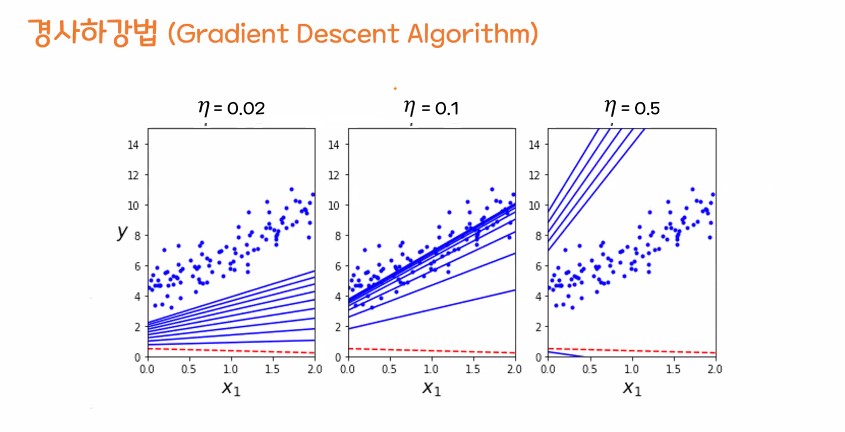
- 경사 하강법이 정말 중요함.

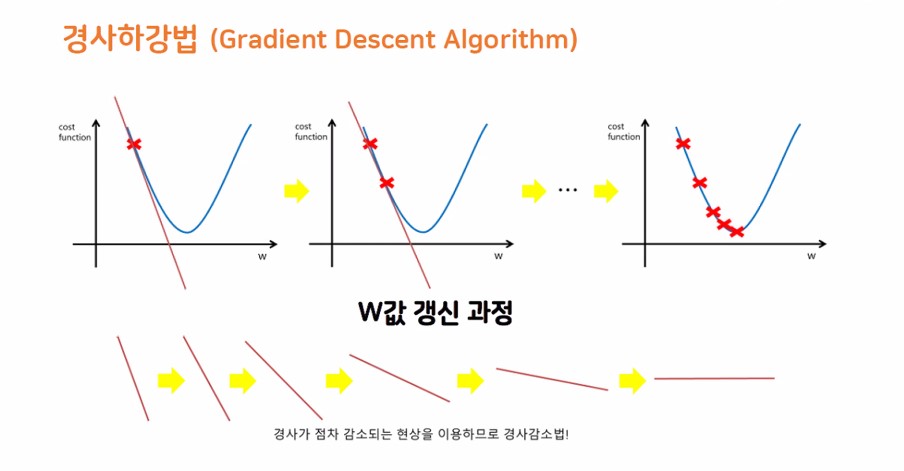
경사 하강법
- 평균 제곱오차가 최소가 되게 하는 최족의 w, b값을 찾는 방법론
- 기계가 스스로 학습한다는 머신, 딥러닝의 개념을 있게 한 핵심 알고리즘


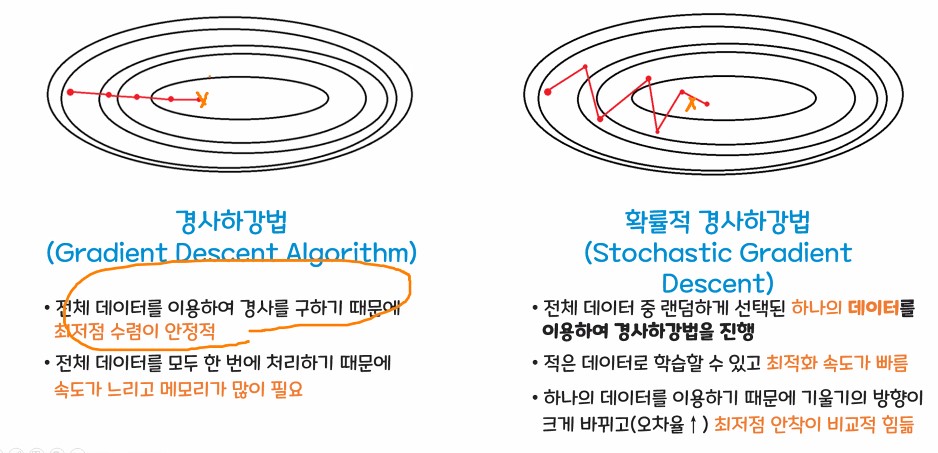
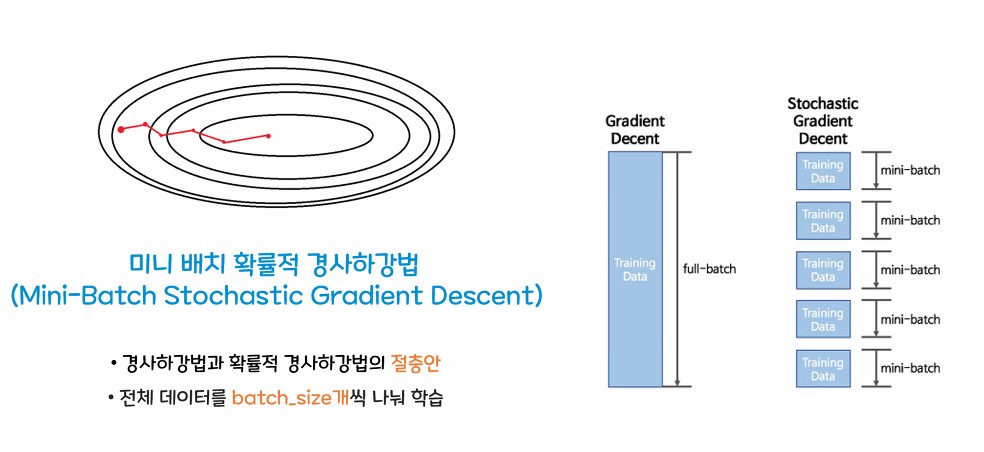
둘의 절충안

상관계수


### 목표
- 선형 회귀를 이용해서 보스턴 주택 데이터를 분석해보자
- 특성 곱을 진행해서 모델의 성능을 끌어 올려보자
- 규제 모델의 사용법을 배워보자(L1(Lasso), L2(Ridge))
# 필요한 라이브러리 불러오기
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# 데이터 불러오기
data = pd.read_csv('./data/boston_housing.csv')
# 필요없는 컬럼 제거
data.drop('Unnamed: 0', axis = 1, inplace = True)
### 데이터 특성정리
**독립변수 : (원인 : 예측값을 설명할 수 있는 변수, 특성)**
- 'CRIM': 범죄율
- 'ZN': 25,000 평방피트를 초과하는 거주지역의 비율
- 'INDUS': 비 소매 상업지역의 면적비율
- 'CHAS': 찰스 강의 경계에 위치하면 1 / 아니면 0
- 'NOX': 대기중 일산화질소 농도
- 'RM': 방의 개수
- 'AGE': 1940년대 이전에 지어진 주택의 비율
- 'DIS': 직업센터와의 거리
- 'RAD': 방사형 도로와의 인접성 지수
- 'TAX': 재산세율
- 'PTRATIO': 선생님과 학생의 비율
- 'B': 인구중 흑인의 비율
- 'LSTAT': 인구중 하위계층의 비율
**종속 변수 : (결과 : 예측하고자 하는 값)**
- 'MEDV': 주택 가격
### 문제와 정답을 나누기!
- 문제 : 주택 가격을 제외한 모든 특성
- 정답 : 주택 가격
# loc / iloc / drop 이 중 한가지 이용
X = data.loc[: , :'LSTAT']
y = data['MEDV']
# shape 확인
X.shape, y.shape
=> ((506, 13), (506,))
### 훈련 셋트와 평가 셋트 구성
- train_test_split() 이용
- test 셋트의 비율 : 30%
- 랜덤시드 : 0
- 주의점 변수수의 순서에 주의하자!
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
X, y,
test_size = 0.3,
random_state = 0)
# shape 확인
X_train.shape, X_test.shape, y_train.shape, y_test.shape
=> ((354, 13), (152, 13), (354,), (152,))
### 모델링
- 선형 회귀 모델을 사용해보자
# 모델 import
from sklearn.linear_model import LinearRegression
# 모델 객체 생성
lr_model = LinearRegression()
# 교차 검증
from sklearn.model_selection import cross_val_score
# cross_val_score(model, X_train, y_train, cv = 몇 조각 등분)
rs = cross_val_score(lr_model, X_train, y_train, cv = 5)
print(rs)
print(rs.mean()) # r2 스코어
# 모델 학습
lr_model.fit(X_train, y_train)
# 모델 예측
pre = lr_model.predict(X_test)
### 여러 평가지표 사용해보기
- MSE / RMSE / MAE / R2score
# 평가지표 불러오기
from sklearn.metrics import mean_squared_error as mse # 평귝 제곱 오차
from sklearn.metrics import mean_absolute_error as mae # 평귝 절대 오차
from sklearn.metrics import r2_score # 결정개수 / r2스코어
# RMSE는 별도로 지원하지 않음 -> 연산이 필요하다.
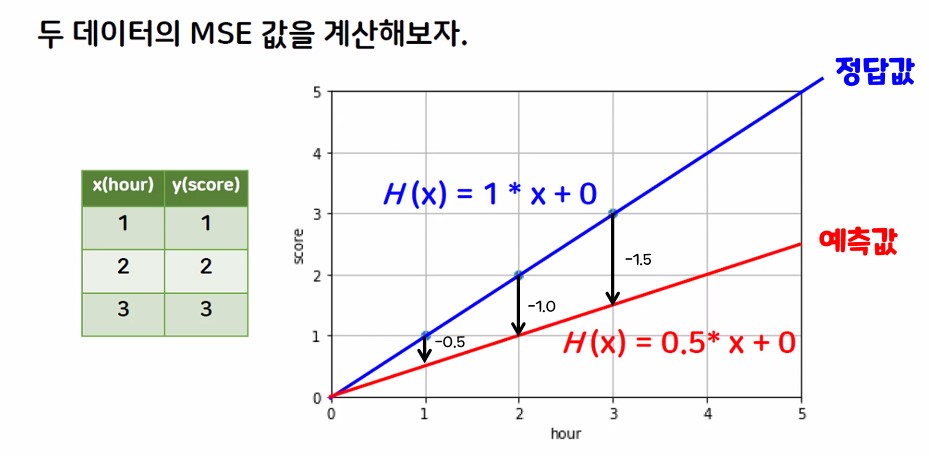
# mse (평균 제곱 오차)
# mse(실제 정답 / 예측 값)
mse(y_test, pre)
# 평균 제곱 오차값이 27.195.....
# 오차가 제곱이 되어있는 상태 -> 오차가 큰지 작은지 확인하기 어렵다 / 성능을 직관적으로 파악하기 어려움
# RMSE (평균 제곱근 오차)
# np.sqrt(mse(y_test, pre))
# np.sqrt : 스퀘어 루트 -> 루트 값 구하는 함수
np.sqrt(mse(y_test, pre))
# 평균 제곱근 오차 5.214....
# 오차의 원래 스케일이지만 직관적으로 성능을 판단하기 어렵다.
# r2_score(결정 계수)
# r2_score(y_test, pre)
r2_score(y_test, pre)
# r2스코어 0~1의 범위를 가지고 있음
# 1에 가까울 수록 성능이 좋다.
# 0에 가까울 수록 성능이 안좋다.
# r2값이 1이면 가지고 있는 X(특성)를 이용해서 Y(정답)을 100% 예측
# r2값이 0이면 가지고 있는 X(특성)를 이용해서 Y(정답)을 0% 예측
# mae (평균 절대 오차)
# mae(실제 정답 / 예측 값)
mae(y_test, pre)
# 평균 절대 오차값이 3.6099....
# 오차가 절대값으로 되어있는 상태
### 모델 평가
- 현재 선형 회귀 모델은 성능이 좋지 못하다.
- 선형 모델의 성능은 데이터가 많아 질 수록 좋아지는 경향이 있다.
- 성능이 좋다는 것은 훈련 데이터를 가지고 학급 시켰을때 성능이 조금 떨어지더라도 새로운 데이터를 받아서 례측할 때 잘 반응하는 것을 의미한다.
### 특성확장 진행하기
- 특성을 확장해서 데이터의 양을 늘려보기
# 원본 데이터가 오염되지 않도록 사본을 만들어서 사용해보자.
# 현재 데이터 프레임의 상태를 똑같이 복사하자
data_copy = data.copy()
# 정답과 연관 관계가 높은 컬럼을 찾아보자
data_corr = data.corr().abs() # 상관관계를 절대 값으로 바꿔주세요
data_corr.sort_values(by='MEDV', ascending = False)
# 상관관계가 높은 놓은 특성 : LSTAT / RM
# 상관관계가 높은 특성으로 학습했을때 특성 확장 전과 후를 비교해서 성능이 얼마나 개선되는지 확인해보자
# 확장 전) 먼저 LASTAT 특성을 가지고 학습 시킨 후 예측을 어떻게 되는지 그래프로 그려보자
model = LinearRegression()
model.fit(X_train[['LSTAT']], y_train)
pre = model.predict(X_train[['LSTAT']])
plt.scatter(X_train['LSTAT'], y_train) # 실제 데이터 분포
plt.scatter(X_train['LSTAT'], pre) # 예측 값 (예측선 확인하기)
plt.show()
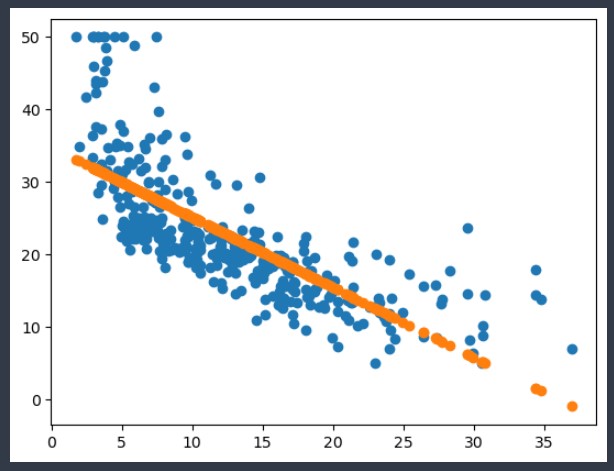
# 확장 후) 원래 LSTAT 컬럼과 확장 특성 LSTAT을 이용해서 학습 후 예측 결과 확인
X_train['LSTAT x LSTAT'] = X_train['LSTAT'] * X_train['LSTAT']
model2 = LinearRegression()
model2.fit(X_train[['LSTAT', 'LSTAT x LSTAT']], y_train)
pre = model2.predict(X_train[['LSTAT', 'LSTAT x LSTAT']])
plt.scatter(X_train['LSTAT'], y_train) # 실제 데이터 분포
plt.scatter(X_train['LSTAT'], pre) # 예측 값 (예측선 확인하기)
plt.show()
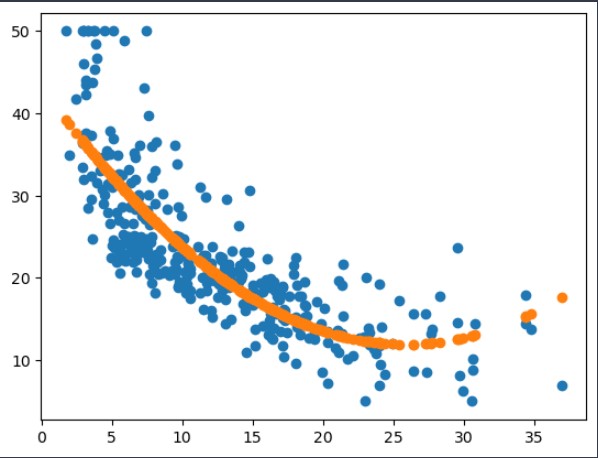
- 다항 회귀의 이해 :
독깁변수의 단항식이 아닌 2차, 3차 방정식과 같은 다항식으로 표현된 것을 다항 회귀
주의)
- 다항 회귀를 선형이 아닌 비선형 회귀로 혼동할 수 있지만, 본질은 선형 회귀인 것을 기억하자.
- 선형 / 비선형 회귀흫 나누는 기준은 회귀계수(w)가 선형 / 비선형인가에 따른 것이지 독립변수의 선형/비선형에 따른 것이 아니다.
# 성능 평가
X_test['LSTAT x LSTAT'] = X_test['LSTAT'] * X_test['LSTAT']
lr_model = LinearRegression()
lr_model.fit(X_train, y_train)
lr_model.score(X_test, y_test)
# 67.3% -> 69.7% = 2.4% 성능개선
# 상관관계가 높은 특성으로 학습했을때 특성 확장 전과 후를 비교해서 성능이 얼마나 개선되는지 확인해보자
# 확장 전) 먼저 RM 특성을 가지고 학습 시킨 후 예측을 어떻게 되는지 그래프로 그려보자
model = LinearRegression()
model.fit(X_train[['RM']], y_train)
pre = model.predict(X_train[['RM']])
plt.scatter(X_train['RM'], y_train) # 실제 데이터 분포
plt.scatter(X_train['RM'], pre) # 예측 값 (예측선 확인하기)
plt.show()
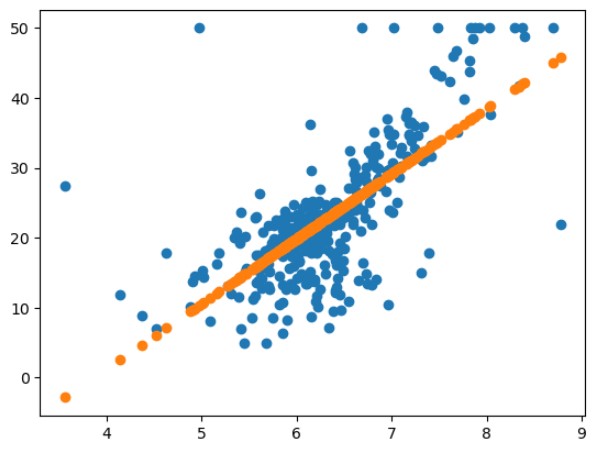
# 확장 후) 원래 RM 컬럼과 확장 특성 RM 을 이용해서 학습 후 예측 결과 확인
X_train['RM x RM'] = X_train['RM'] * X_train['RM']
model2 = LinearRegression()
model2.fit(X_train[['RM', 'RM x RM']], y_train)
pre = model2.predict(X_train[['RM', 'RM x RM']])
plt.scatter(X_train['RM'], y_train) # 실제 데이터 분포
plt.scatter(X_train['RM'], pre) # 예측 값 (예측선 확인하기)
plt.show()
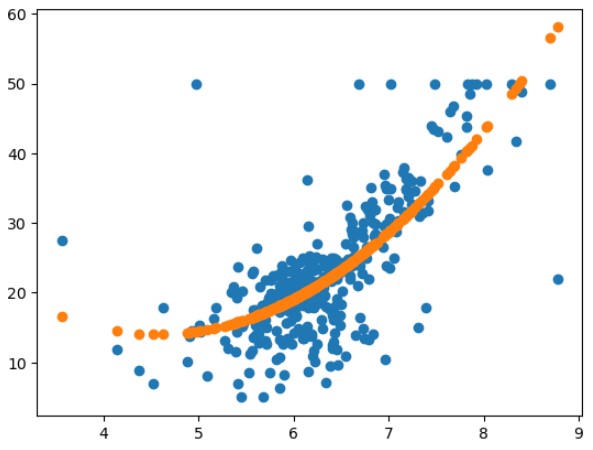
# 성능평가
X_test['RM x RM'] = X_test['RM'] * X_test['RM']
lr_model = LinearRegression()
lr_model.fit(X_train, y_train)
lr_model.score(X_test, y_test)
# 67.3% -> 69.7% = 2.4% 성능개선
=> 0.7460776611187953
# 가설 : 특성 확장이 진행될때마다 성능이 좋아지는 것을 확인
# 전체 특성을 확장 시킨다면 성능이 월등히 좋아질까?
X_train.drop(['LSTAT x LSTAT', 'RM x RM'], axis=1, inplace=True)
X_test.drop(['LSTAT x LSTAT', 'RM x RM'], axis=1, inplace=True)
# 훈련 / 평가셋 복사하기
ex_X_train = X_train.copy()
ex_X_test = X_train.copy()
# 훈련셋 특성 확장
for col1 in X_train.columns: # 13번 반복
for col2 in X_train.columns: # 13번 반복
ex_X_train[col1 + 'x' + col2] = X_train[col1] * X_train[col2]
ex_X_train.shape
ex_X_test.shape
# 모델링
lr_model = LinearRegression()
lr_model.fit(ex_X_train, y_train)
lr_model.score(ex_X_test, y_test)
lr_model.score(ex_X_train, y_train)
=> 0.9517246762476054
선행 회귀 - 직선의 형태를 가지고 1차식으로 연속적인 실수 값을 예측하는 분야
-
y = wx + b
-
x = 독립변수 / 데이터의 특성 / 컬럼
-
y = 종속변수 / 예측값 / 예측한 정답
-
w = 가중치 / 특성의 정답 관여율
-
b = 절편 / 편향
-> y = wx 라는 회귀직선을 y축 방향으로 얼마나 수직평행 이동 시키는지? -
다중 회귀 함수
y = wx + wx + wx + ..... + wx + b
- 평가 지표
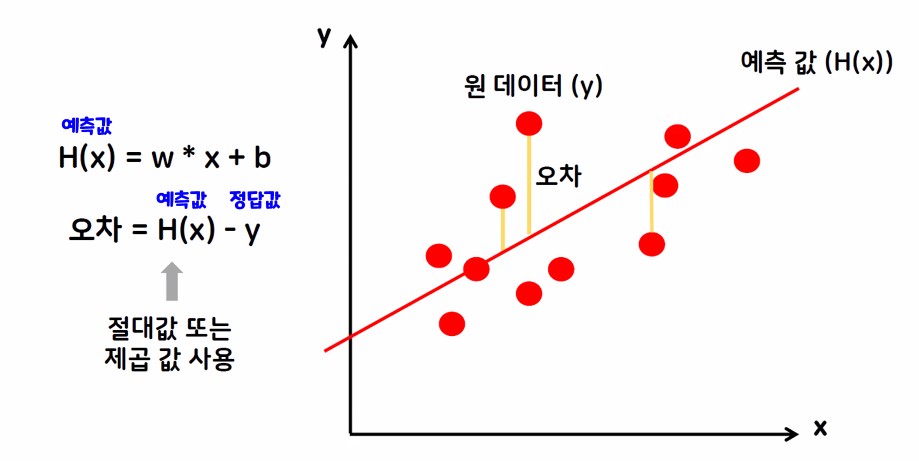
- 오차 -> H(x) - y
- H(x) = 예측값 -> y=wx+b -> 오차는 절대 값이나 제곱 값을 사용하는 경우가 많다.
-> 음수로 인해 연산이 잘못되는 것을 방지하기 위해서
- 한글 뜻을 뒤에서 해석하며 풀이하면 접근이 쉬워짐
mse -> mean squared error (평균 제곱 오차)
rmse -> root mean squared error (평균 제곱근 오차)
mae -> mean absolute error (평균 절대 오차)
mape -> mean absolute percentage error (평균 절대비율 오차)
r2score -> 결정계수
선형 회귀의 최종 목표
-> mse가 최소가 되는 최적의 가중치와 편향을 구한다.
최종 목표를 달성하기 위한 방법론
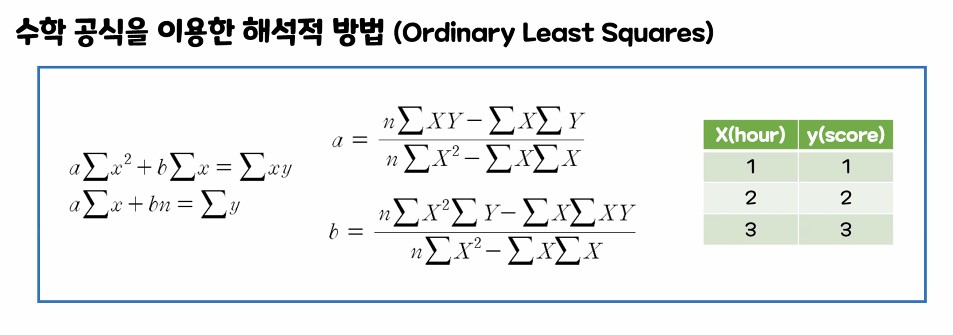
1. 수학공식을 이용한 해석적 방법 -> 연립방정식
2. 경사하강법 -> 중요 / 엄청중요 / 겁나중요
