Intro
CNN
- LeCun, 1988년 제안한 뉴럴 네트워크의 한 종류
- 각 pixel의 값이 feature가 됨. 즉 grid-like 구조에 특화되어 있다.
- 시계열 데이터 : 1d grid
- 이미지 데이터 : 2d grid + RGB 채널
- Convolution operation을 수행
Motivation : 특징
- sparse한 connection을 가진다. ( 이미지의 각 feature을 다 연결하면 파라미터가 너무 많아짐 )
- 파라미터 공유 -> 같이 update됨
- 공간적인 데이터. 공간상 위치가 정보를 가짐
Fully Connected Layer와 비교
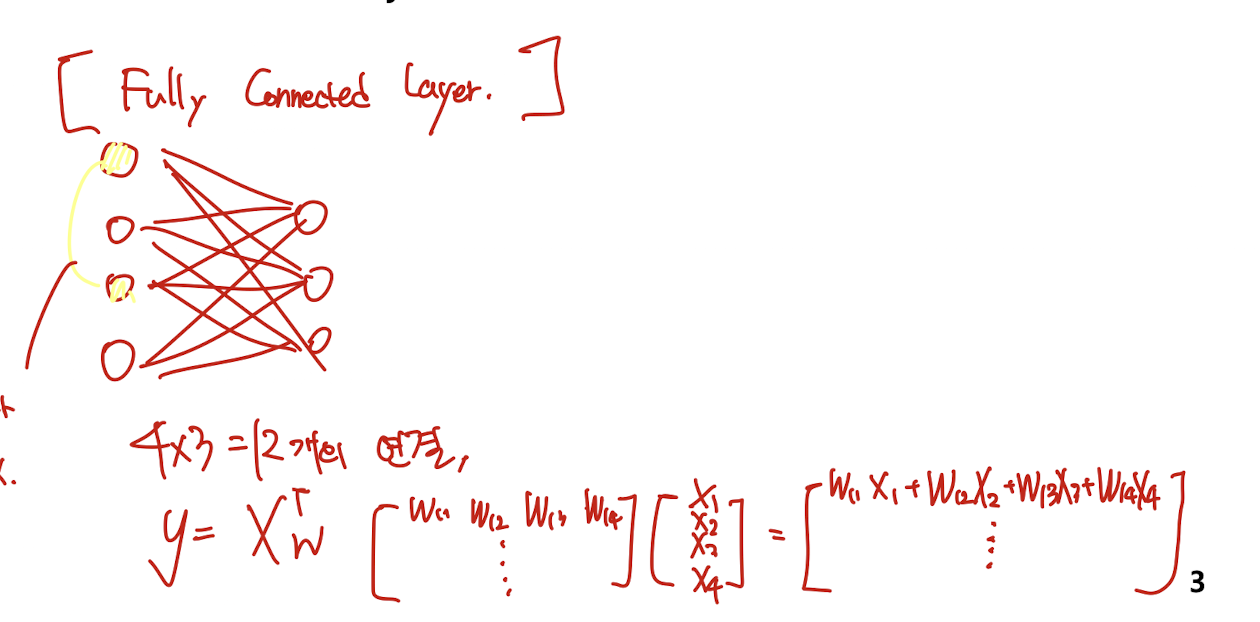
- 전체가 다 연결되어 있음.
- 각각 모두 다른 파라미터를 가짐
- 각 노드가 완전 독립적이라 순서가 상관이 없다.
Convolutional Neural Network
Convolution Operation
- Convolution : 주로 신호처리에서 많이 쓰이는 연산
-
원래의 convolution 연산
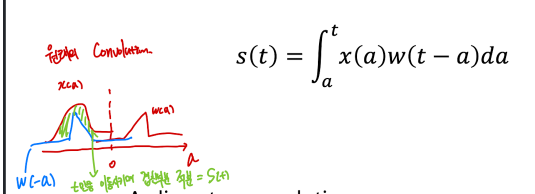
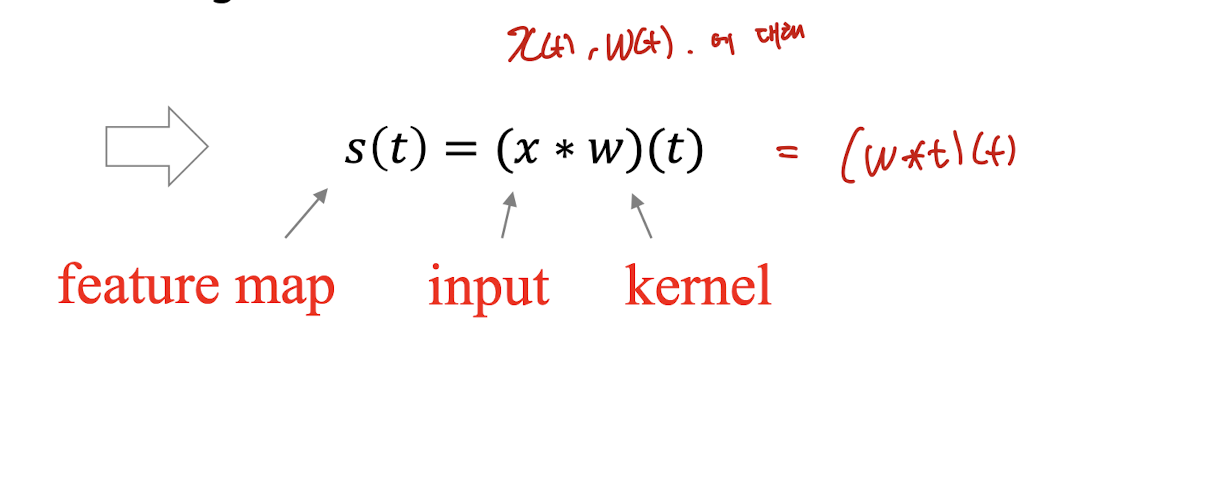
-
CNN에서의 convolution
- Input, Kernel 모두 finite한 값- 좌우반전 시키지 않음
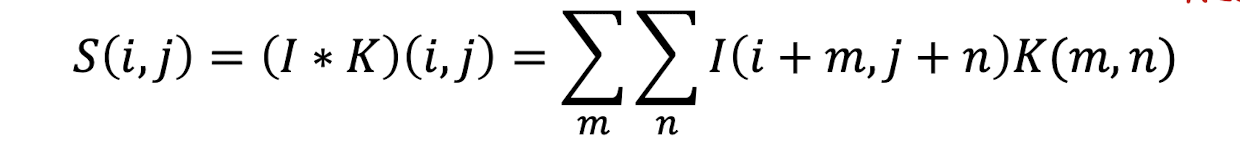
- 좌우반전 시키지 않음
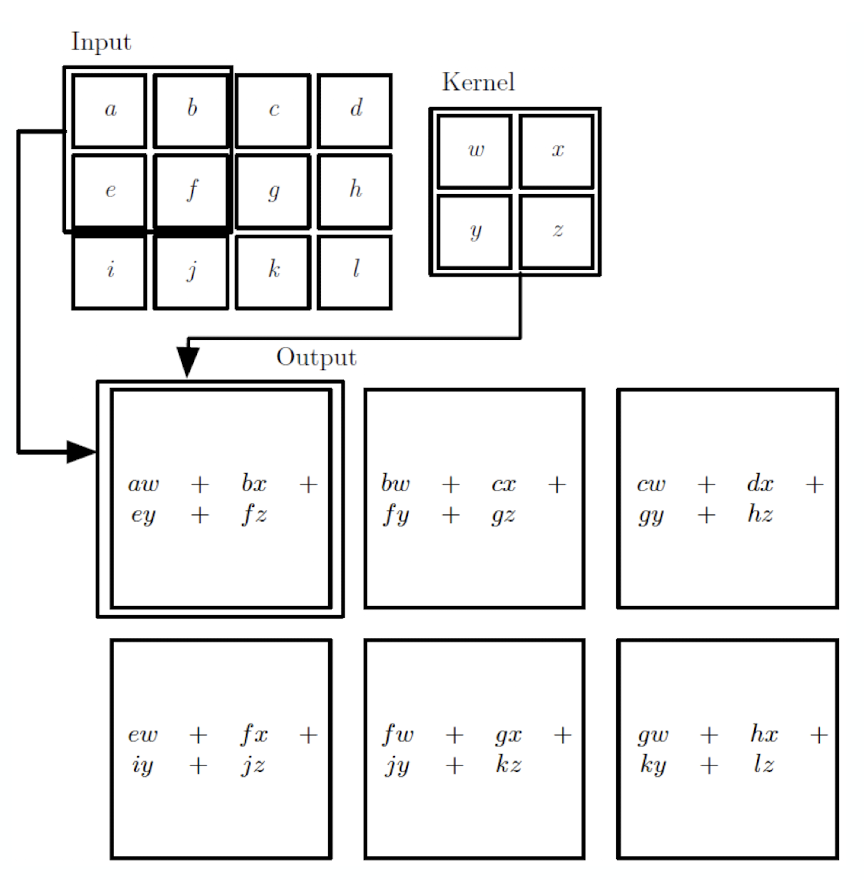
Example
4 * 4 input, 2 * 2 Filter
최종 결과

FC와 비교
FC : 16 -> 9 로 가는 layer, 즉 16 * 9 개의 연결(가중치)이 필요하다.
Convolution Layer
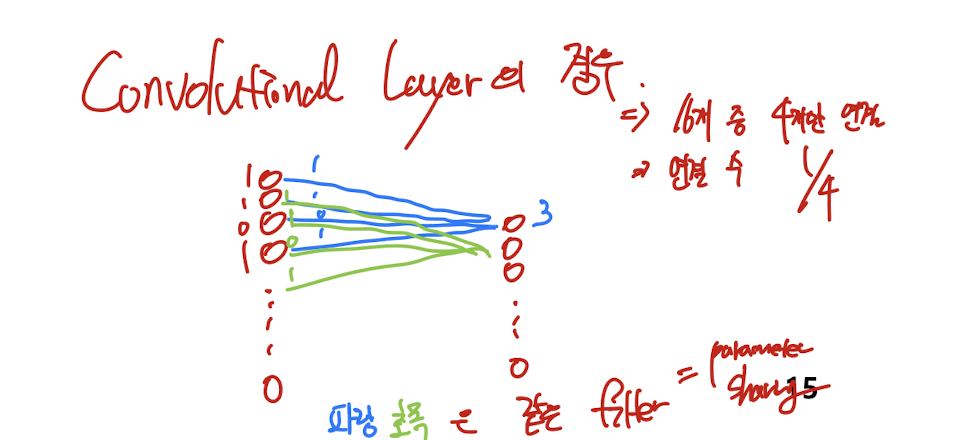
General expression
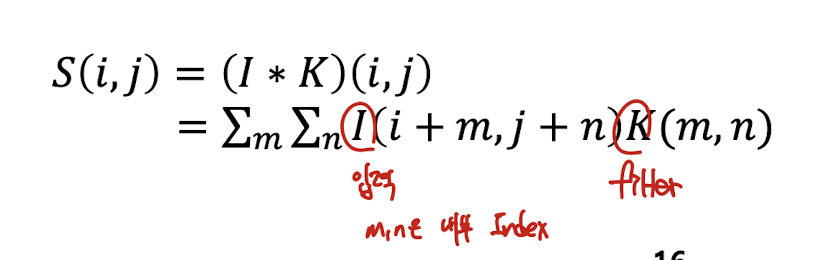
Convolutional operation for multi-channel inputs
기본적으로 컬러 이미지는 3개의 채널로 표현됨. R,G,B
3 dimensions : width, height, depth(R,G,B or 흑백일 경우 1개)
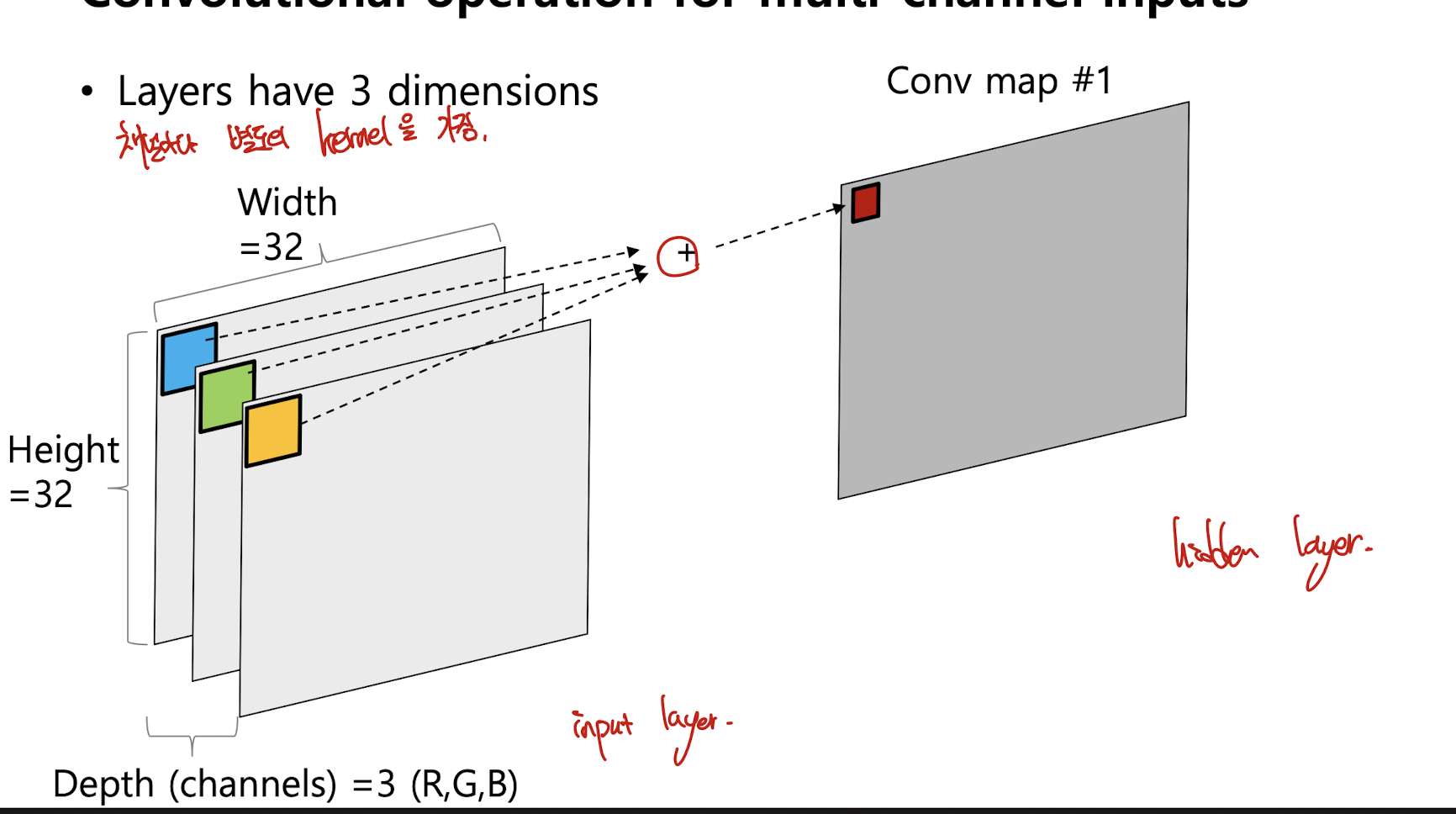
각 input channels마다 각각의 kernel이 존재한다. ( 위 그림에서는 파랑, 초록, 노란색 정사각형 )
각 channel의 convolution 결과를 Sum하여 한 개의 output을 출력
kernel (필터) 의 사이즈가 5 * 5 라면,
kernel의 weight 개수는 5 * 5 * 3 으로 결정할 수 있음 (파랑,초록,노란색 정사각형)
이때 output channel이 여러개라고 하면, 각 output channel은 각각의 kernel을 가진다.
예시
input channel 3, output channel 12개라면, 총 36개의 kernel이 필요하다.
kernel size = 5 * 5 라고 하면
총 필요한 weight의 개수는
36 * 5 * 5
example
앞의 괄호는 size이다.
input : ( 7 * 7 ) * 3
filter : ( 3 * 3 ) 6 ( input * output )
output : ( 3 * 3 ) * 2
bias : 각 output channel 별로 존재.
cf) 본 summary에서는 kernel ( fiter ) 의 개수를 6이라고 이해하는데,
( 3 * 3 * 3 )* 2 처럼, kernel의 개수 == output channel의 개수 라고 진행하는 강의와 논문도 많다.
Convolution operation
합성곱 연산은 데이터와 합성곱 filter(kernel)간의 행렬곱(linear operation)이다.
MLP(fc layer)와의 차이로,
- 필터는 격자 형태의 국소 데이터에 영향을 미친다. 즉 모두와 연결되지 않는다. ( 희소 연결 )
- 필터는 이미지의 모든 픽셀에 대해 사용된다. ( 파라미터 공유 )
- 필터는 원본 이미지에 대한 하나의 표현을 찾는다. 같은 입력에 대해 별도의 representation
Motivation : Sparse interactions
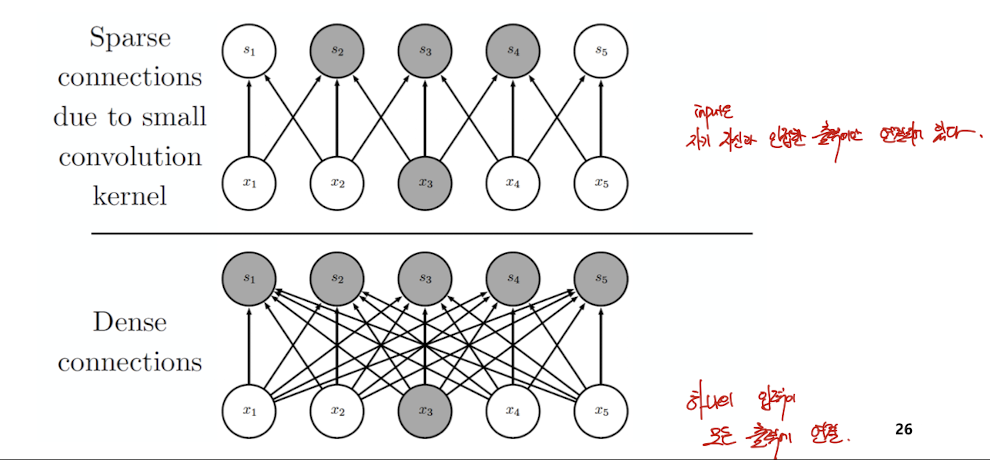
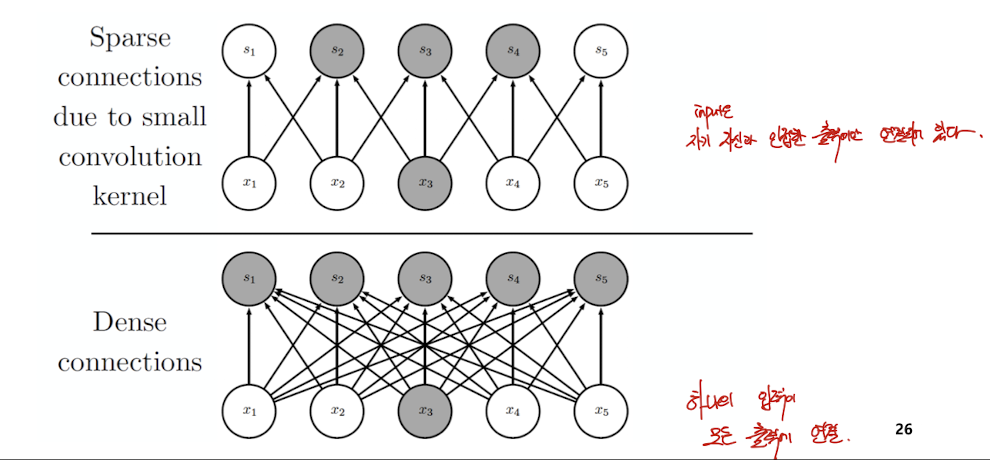
주변에 있는 몇개 노드에서만 신호 전달 - Receptive field : 수용장
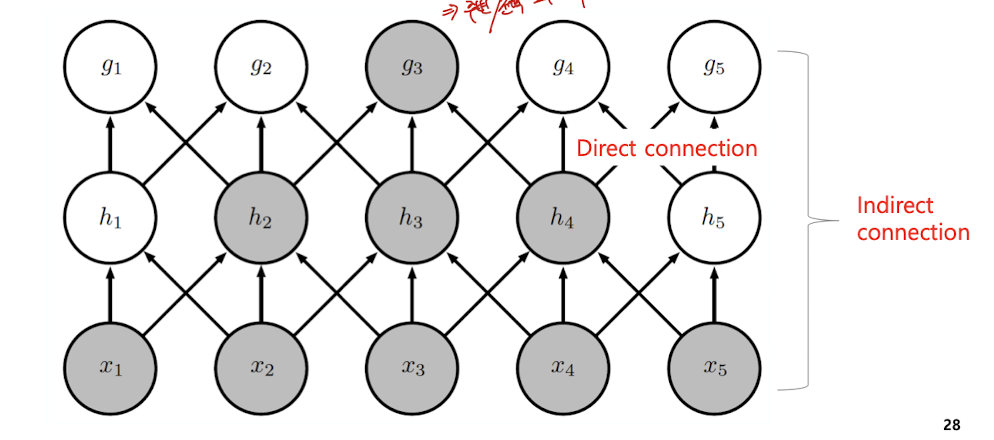
하지만 이러한 layer을 쌓으면, 결국엔 모든 input으로부터 영향을 받는다.
이러한 연산을 통하여, 파라미터(연결)과 연산이 줄어든다. 따라서 메모리나 CPU 측면에서 이득
example
Receptive field size를 한번 확인해보자.
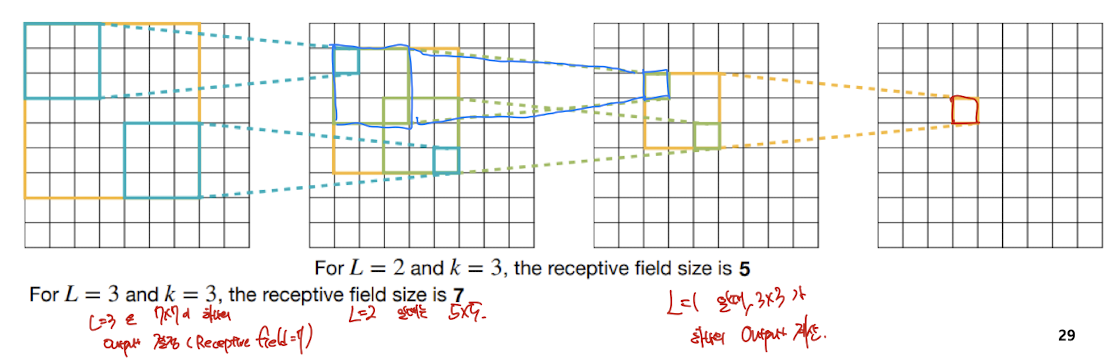
하나의 출력을 내는데, Receptive field?
L = 1 일때는 3 3
L = 2 일때는 5 5
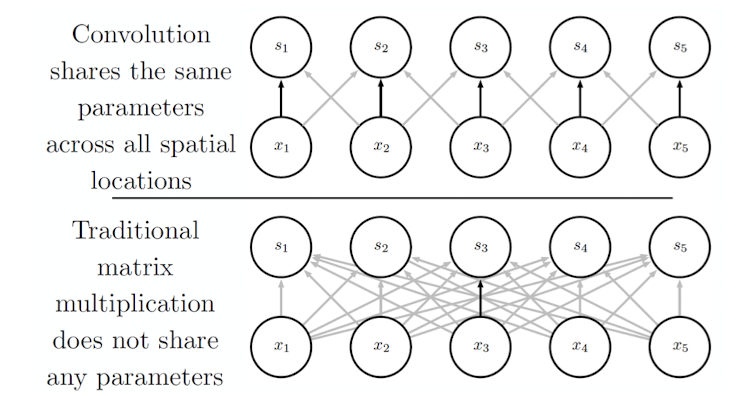
Motivation : parameter sharing
FC, MLP에서는 가중치 행렬의 각 요소가 정확히 한 번만 사용된다. 서로 다 독립적
합성곱 신경망에서는 하나의 채널에서 같은 커널 사용
- 커널의 각 요소는 입력의 모든 위치에서 사용
- 각 위치마다 별도의 파라미터를 학습하지 않음
- 대신 하나의 집합만 학습
장점 : 메모리 절약, 정규화 효과
Motivation : Equivariant representation
등변성, input이 변하면 output도 같은 형태로 변한다. 즉 함수의 방향 순서를 바꿔도 무방하다.
수식적으로는 다음과 같이 정의된다.
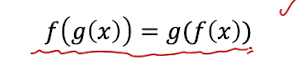
CNN에서
입력에 대한 변화가 있을 때 (이미지를 자른다거나, 약간의 shift)
입력 변화 -> CNN
CNN -> 입력 변화
같은 결과를 낸다.
따라서 노이즈에 강인한 특성을 가진다.
Pooling
sub sampling, 주변값을 대푯값으로 표현하여 size를 줄인다.
- 비선형 활성화 값의 출력을 변형하는 과정이다.
- 신경망의 특정 위치에서의 출력을 그 주변 출력들의 요약 통계치(최대값, 평균값)로 대체
- Max pooling : 정해진 영역 내에서 가장 큰 값을 고름
- average pooling(영역의 평균값), L2 pooling, weighted average pooling ..
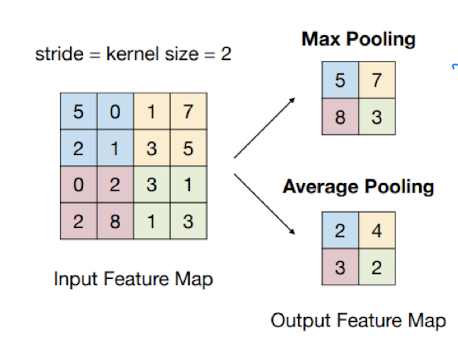

입력의 크기가 작든, 크든 출력의 크기는 일정하게 맞춰야 한다.
크기가 큰 image 처리를 위하여 size를 줄여줄 필요가 있다.
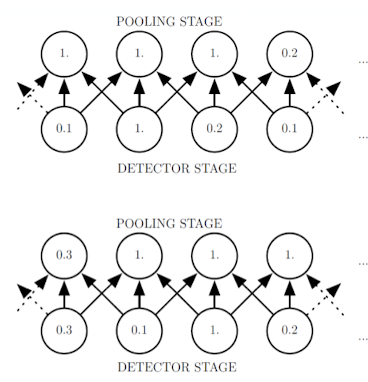
사이즈를 단순히 줄이게 되면 정보를 줄이게 됨. 근데 어느정도 괜찮다. 큰 값이 출력값에 영향을 크게 준다. Max 값을 전달한다는 측면에서 괜찮다.
그리고 약간의 input 변화에는 영향을 덜 받는다.
ex) 약간의 노이즈 영향을 받지 않음
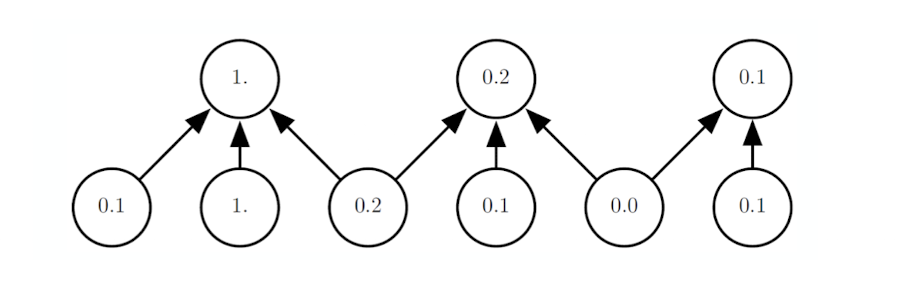
k -> 1
중간 중간 줄여주는 것이
연산 측면에서의 효율성
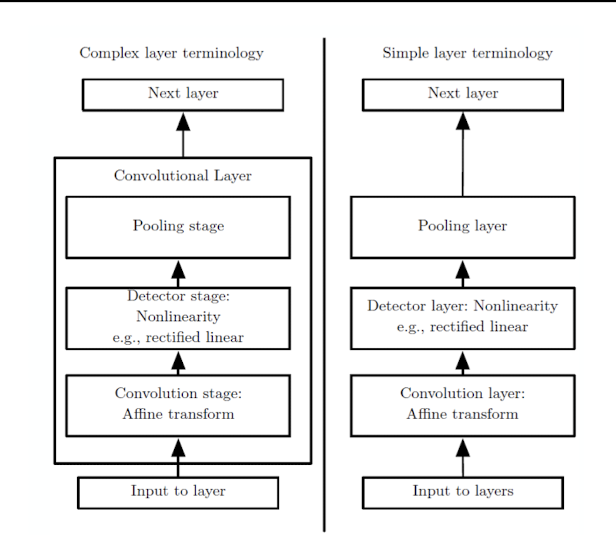
많이 쓰이기 때문에
컨볼루션 연산, 논리니어 액티베이션, 풀링까지 묶어서 컨볼루션 연산이라고 하는 경우가 대부분
Variants of the basic convolution function
컨볼루션 연산의 변형들
Stride Convolution
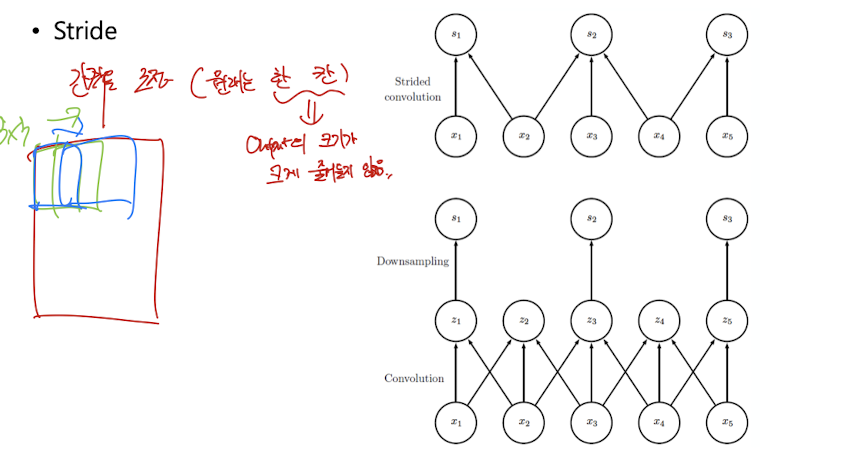
원래는 kernel이 한 칸씩 움직임. output의 크기가 크게 줄어들지 않는다.
stride를 높이면 size가 줄어듦
receptive field를 적은 Layer 수로 크게 키울 수 있다.
입력과 출력 size 계산하는 공식
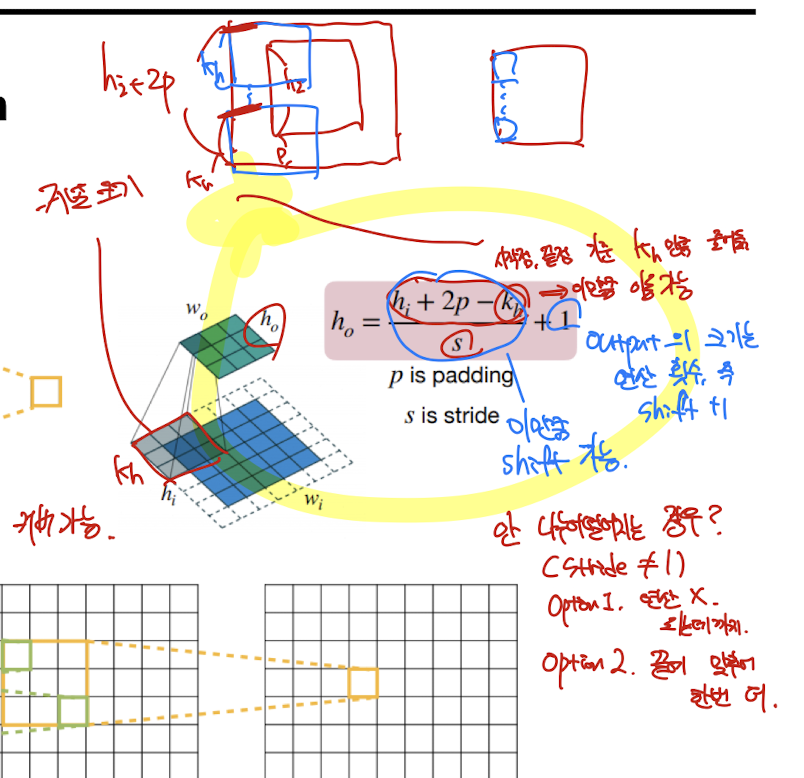
출력(feature map)의 크기를 계산하는 공식
각 기호의 의미:
- : 출력(feature map)의 높이 (output height)
- : 입력 데이터의 높이 (input height)
- : 패딩(padding) 크기 (입력 데이터의 가장자리에 추가하는 값의 폭)
- : 커널(필터)의 크기 (kernel size)
- : 스트라이드(stride, 필터가 한 번에 이동하는 칸 수)
왜?
예시:
입력 이미지 높이 = 32, 패딩 = 1, 커널 크기 = 3, 스트라이드 = 1일 때,
= (32 + 2* 1 - 3)/1 + 1 = (32 + 2 - 3)/1 + 1 = 31/1 + 1 = 32
즉, 출력의 높이는 32
Zero-padding
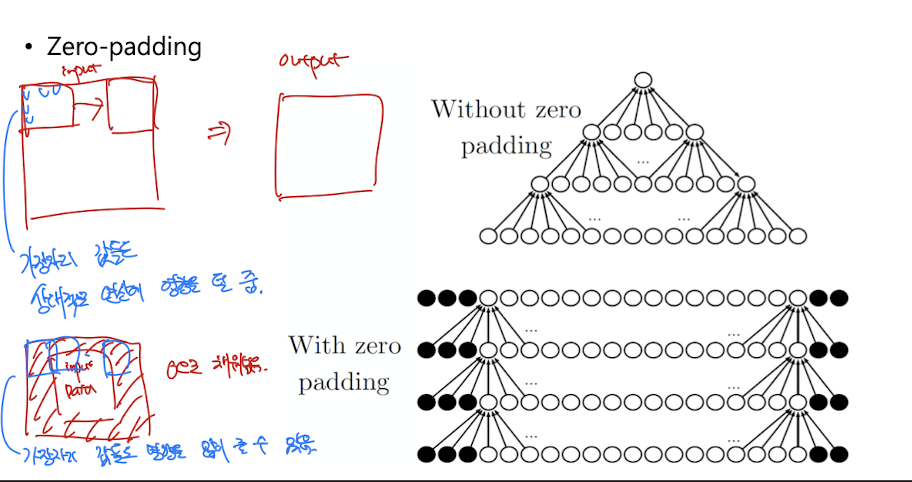
가장자리에 있는 값들은 output에 영향을 상대적으로 덜 준다. 한번만 연산에 반영하기 때문
다른값들은 여러번 통과
또는 입력과 출력의 size를 맞추기 위하여 적용
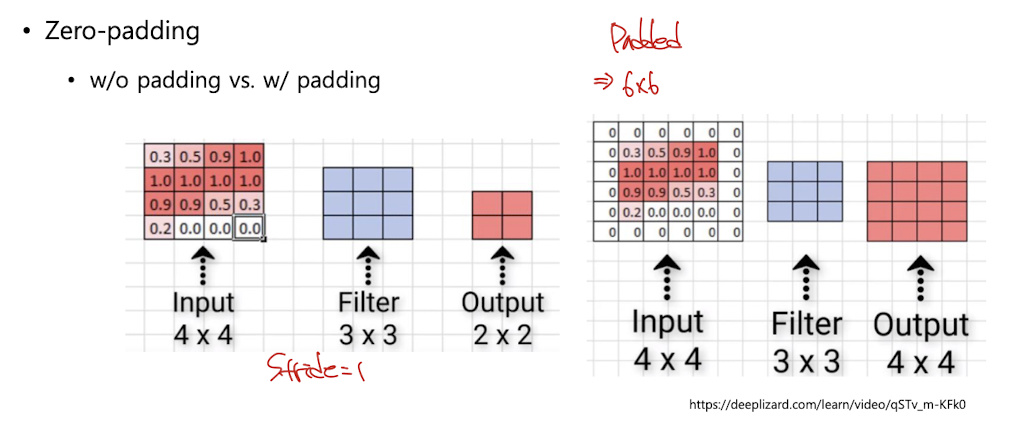
그래서 가장자리에 0을 다 채워넣음.
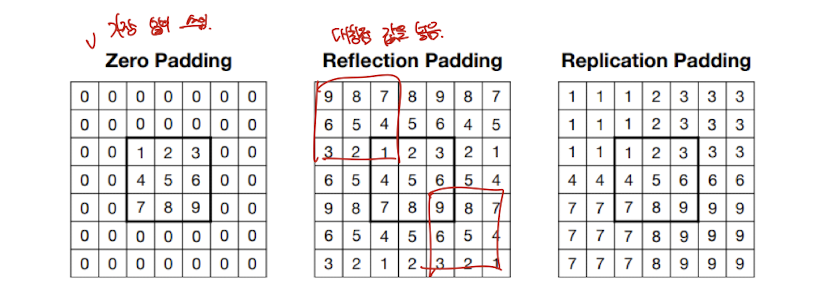
말고도 여러가지 padding 값들이 있다.
어느정도 의미있는 값을 넣는 Refection Padding, Replication Padding
마이너한 주제들
Unshared Convolution ( local connection )
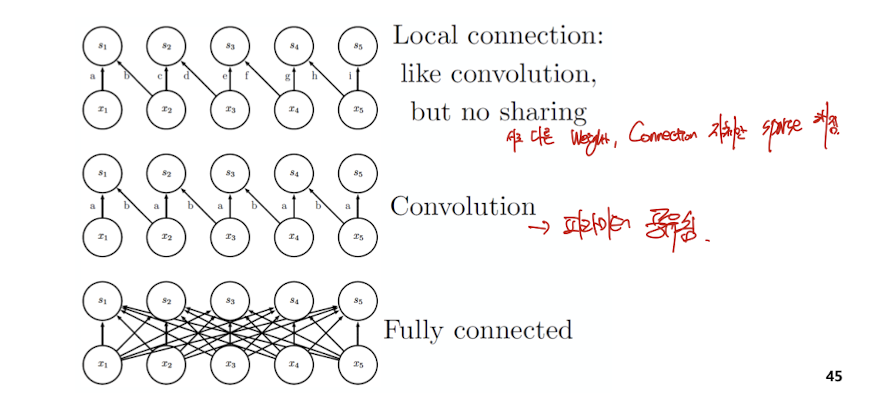
엄밀하게는 Convolution이 아니긴하다. ㅇㅇ
Tiled convolution
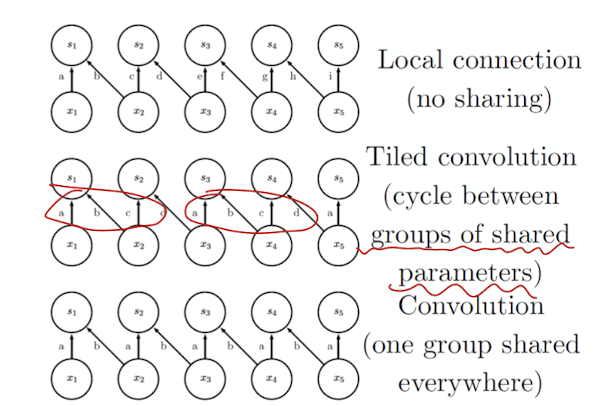
shared parameter 즉 하나의 channel에 대하여 filter가 여러개임. 그걸 번갈아써가면서 사용
CNN Architectures
CNN은 효율적인 구조를 가지면서도 매우 높은 정확도를 달성함. 다양한 구조에 대해 배워보자.
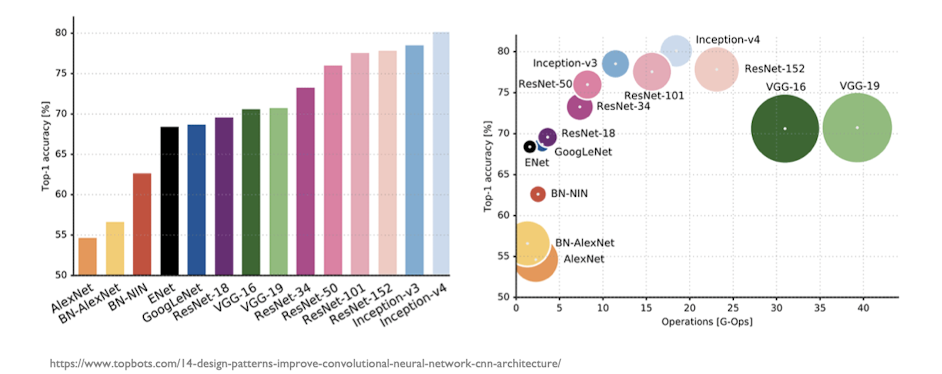
Remarkable CNN architectures
LeNet
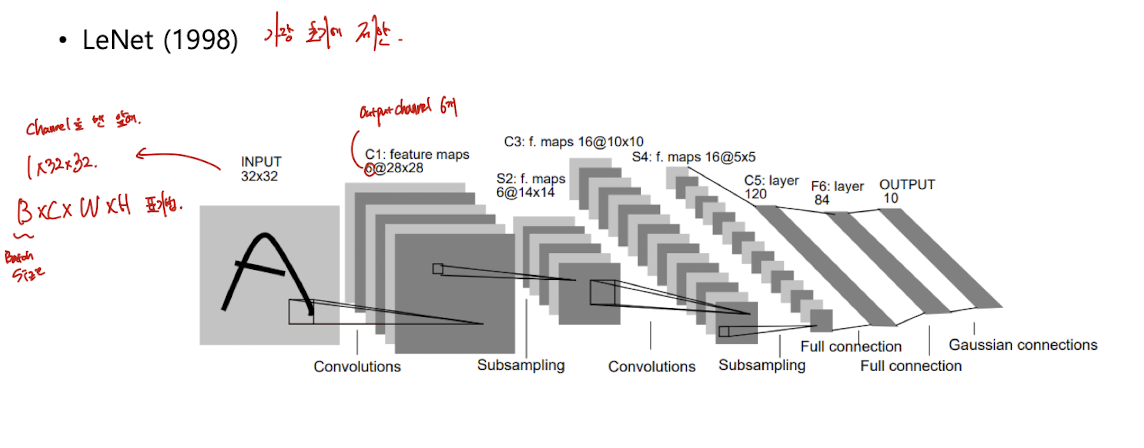
98년에 가장 초기에 제안됨.
subsampling과 Convolution 사용
하나의 1 32 32 channel ( 지금은 이런식으로 표기 )
cf)
pytorch는
Batch size * # of channel * width * height 로 표기
AlexNet
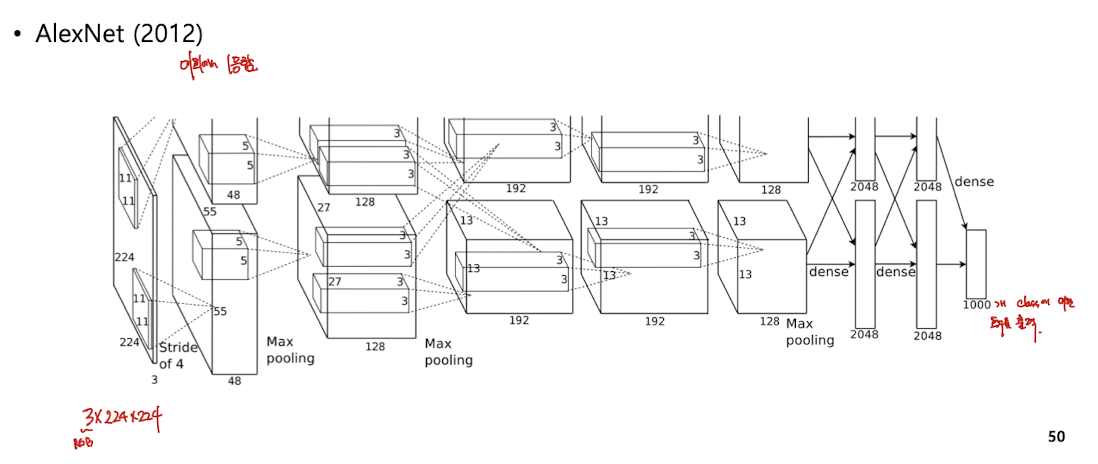
Max pooling 사용
grouped convolution : 한 채널을 절반씩 grouping 하여, 같은 그룹끼리만 convolution. 중간에 cross하기도 함
예시
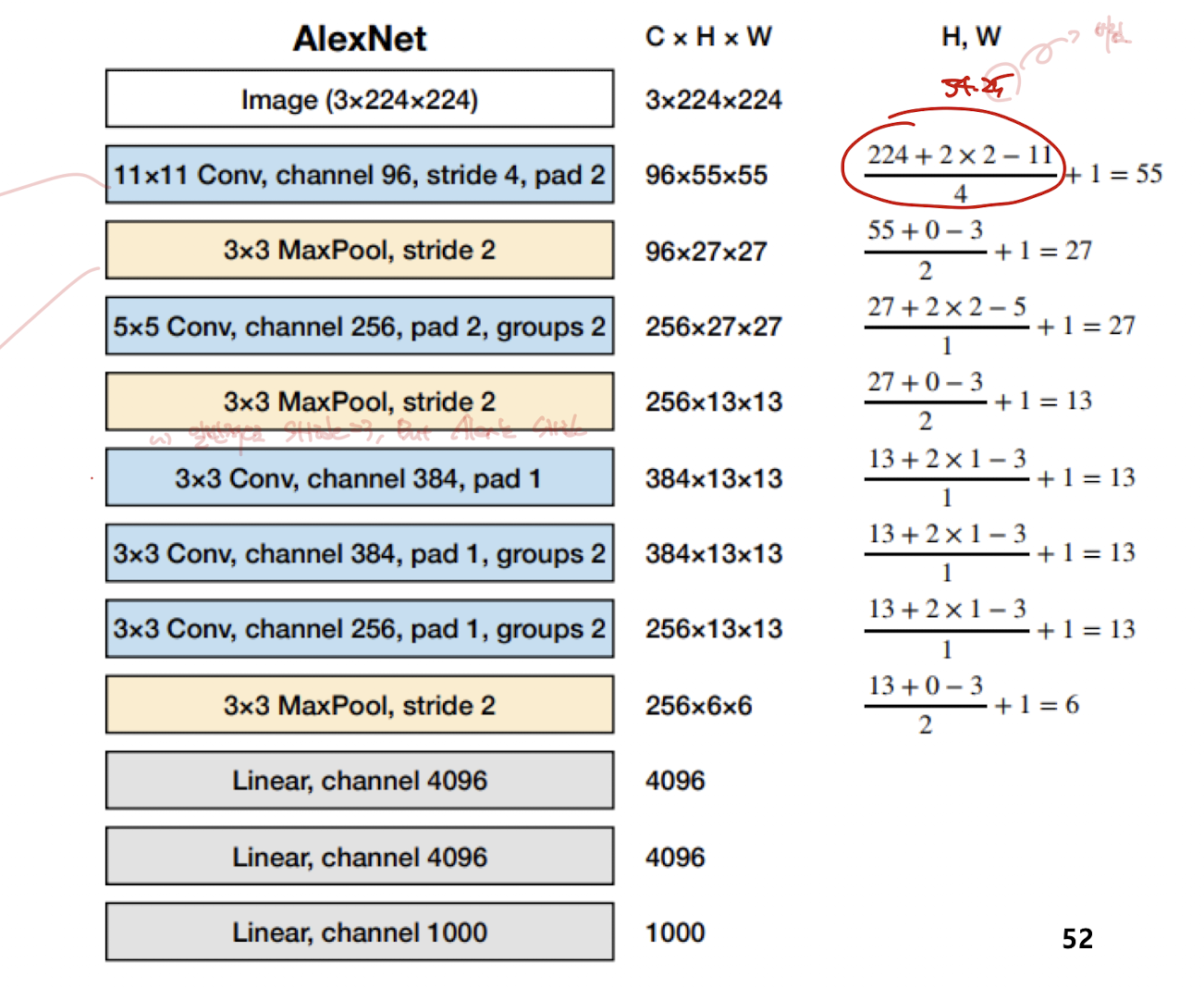
input image : 3 * 224 * 224
11 * 11 convolution 수행, output channel은 96이고 stride 4, pad 2
총 파라미터 개수는 11 * 11 * 3 * 96
output 채널의 크기는
224 + (2 * 2) - 11 / 4 + 1 = 55 (55.25에서 버림)
따라서 두번째 레이어는 96 55 55
3 * 3 Max pooling (보통 stride는 3으로 가져감) 여기서는 stride 2
결국 Max Pooling도 size 3 * 3 인 커널에 적용시킨다고 생각하면 된다. 공식넣어보셈
96*27*27
parameter의 개수는 해당 layer의 input channel과 output channel, 그리고 Kernel size를 곱해주면 됨.
Grouped convolution인 경우
input channel : 96
output channel : 256
2 group 일때
원래는 256* 96 * 5* 5 임.
근데 2개로 각각 인풋 아웃풋 채널을 쪼갰음. 즉 128, 48
이러한 파라미터 set이 2개니까
1/2 1/2 2 = 1/2
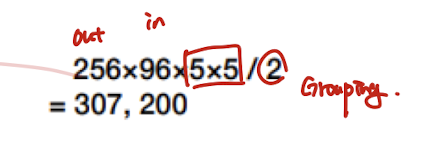
그냥 끝에 나누기 2라고 써주면 된다.
VGGNet
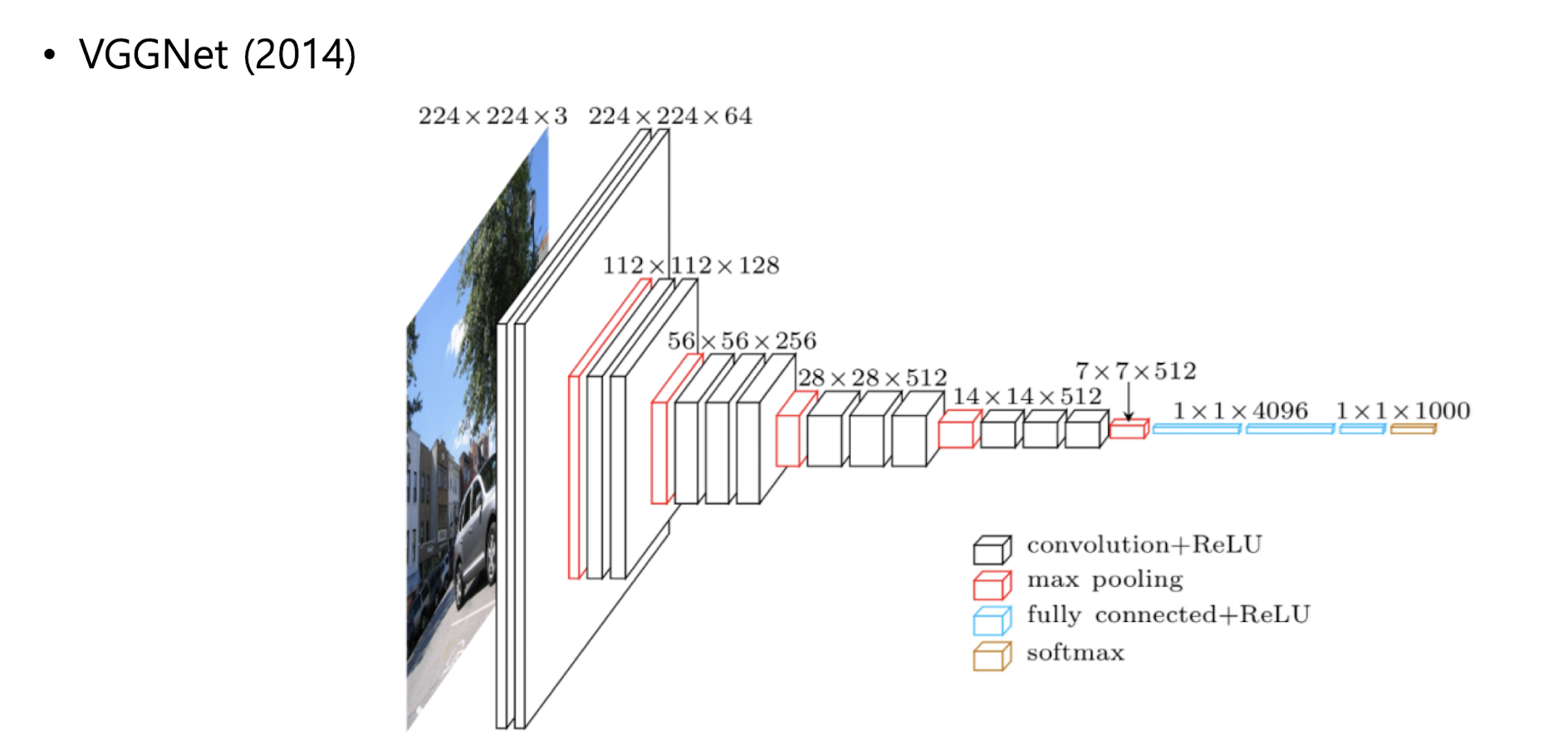
3 *3 convolution과 2*2 풀링을 반복
VGG-16 ( 16개 레이어 )
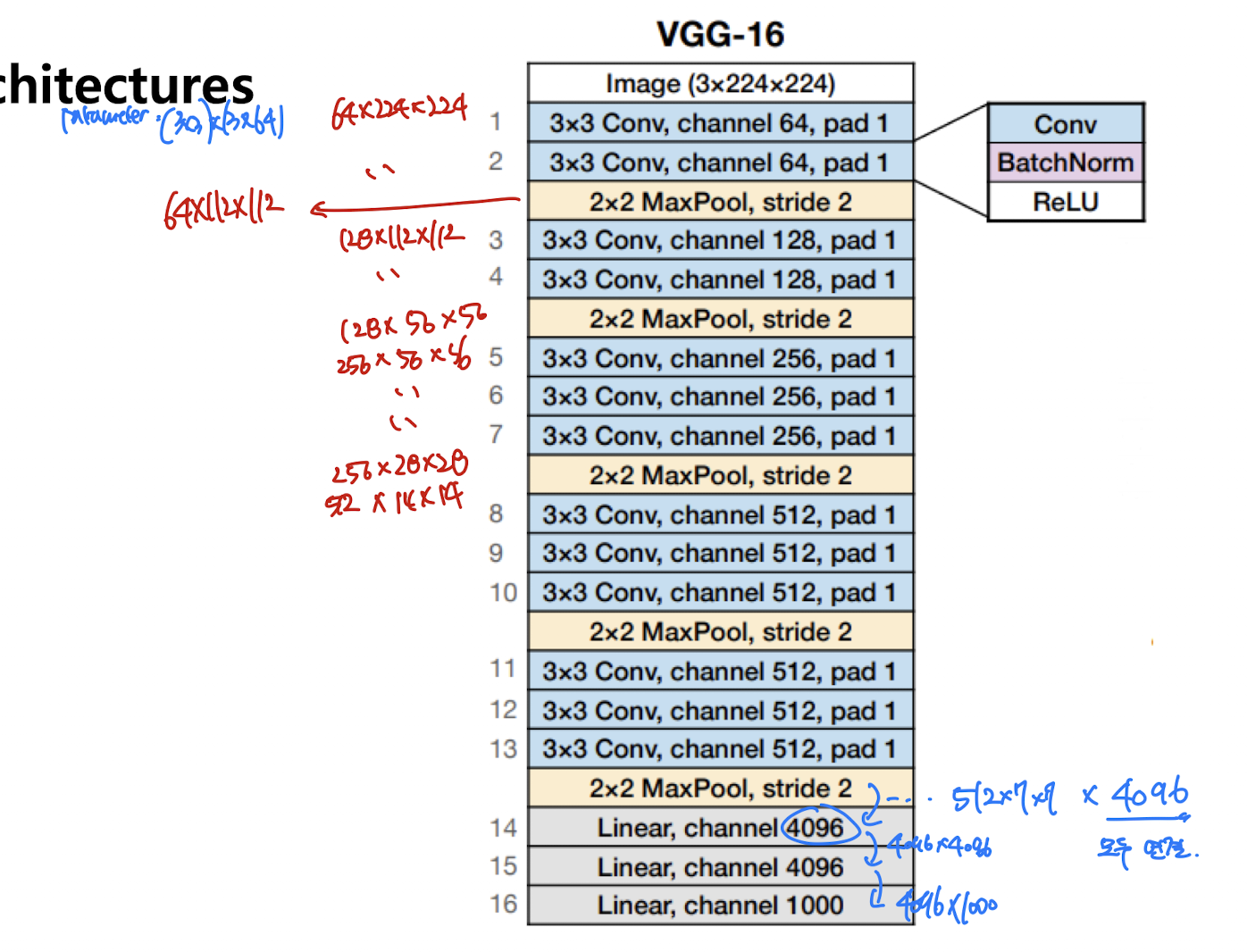
계산은 한번 직접 해보는 것이 좋을 듯 하다.
GoogleNet
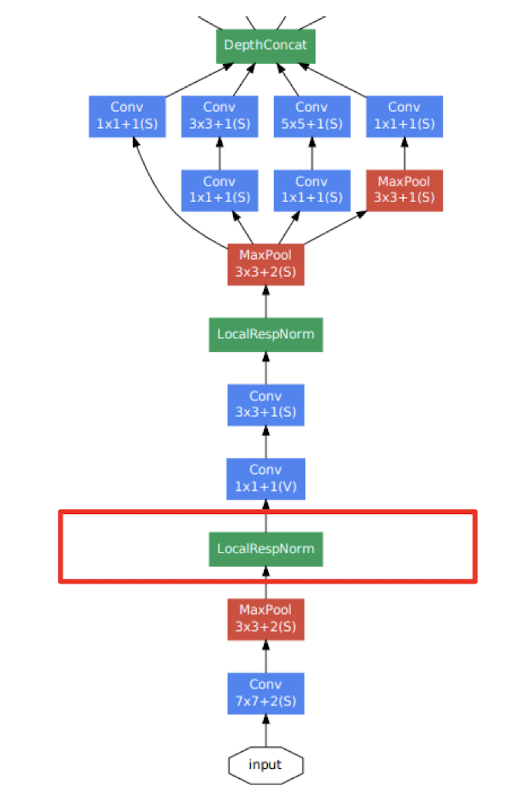
Local response normalization, LRN : 가장 강하게 활성화된 뉴런이 다른 feature map에 있는 같은 위치의 뉴런을 억제. 여러 channel에서 같은 위치의 뉴런들이 경쟁하게 하여 특정 채널이 강하게 활성화되는것을 방지한다.
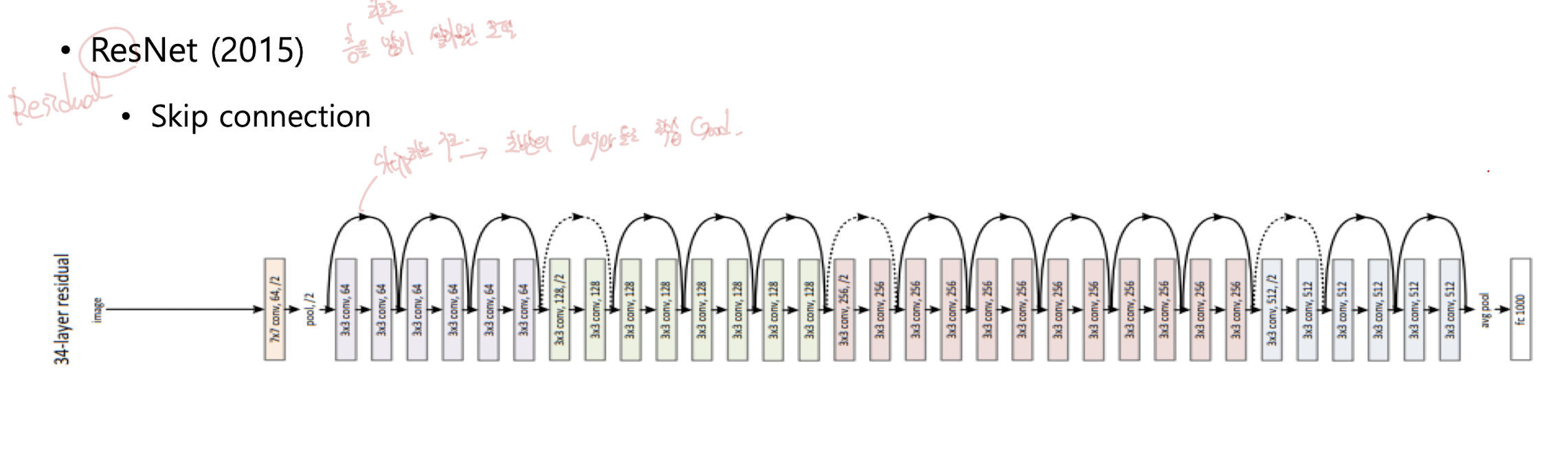
최초로 층을 많이 쌓아올린 모델
SKIP connection 즉 일반적인 합성곱 연산 블록을 여러 층 쌓는 대신에 입력을 다음 블록의 출력에 더해주는 구조로, 입력이 다음 블록을 건너뛰어 더해진다.
-> 기울기 소실, 기울기 폭주 문제 완화, 더 깊은 네트워크 학습 가능
잔차 학습(residual) : 입력 - 출력, 즉 잔차만 학습하면 되므로 최적화가 더 쉬워진다.
ResNet
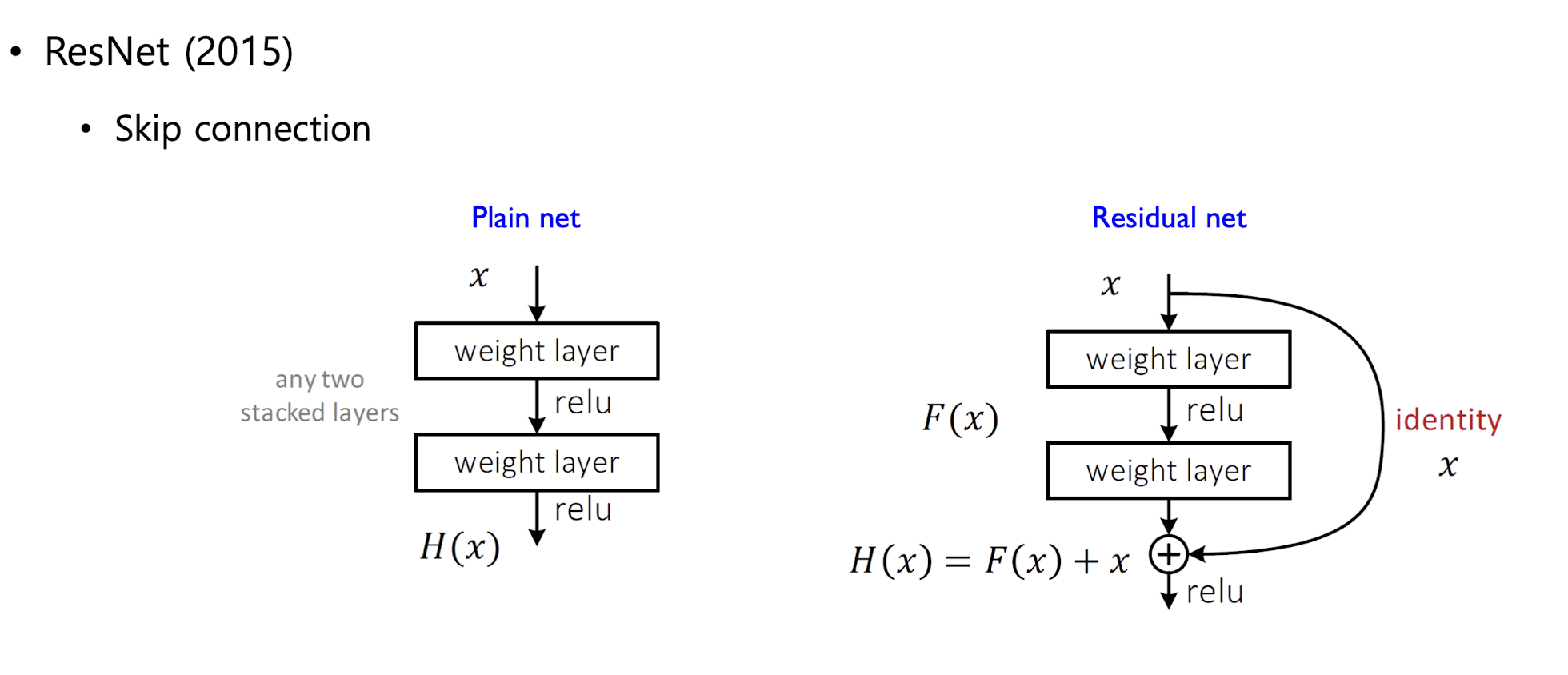
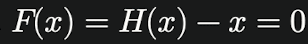
왼쪽 그림은 일반 네트워크
오른쪽 그림은 residual connection.
입력 x는 아래로 위회하여 마지막 출력에 더해진다.
기울기 소실 문제 크게 완화, 네트워크가 입력과 출력의 차이만 학습하면 되기 떄문에 깊은 네트워크도 효율적으로 학습할 수 있음
ResNet-50
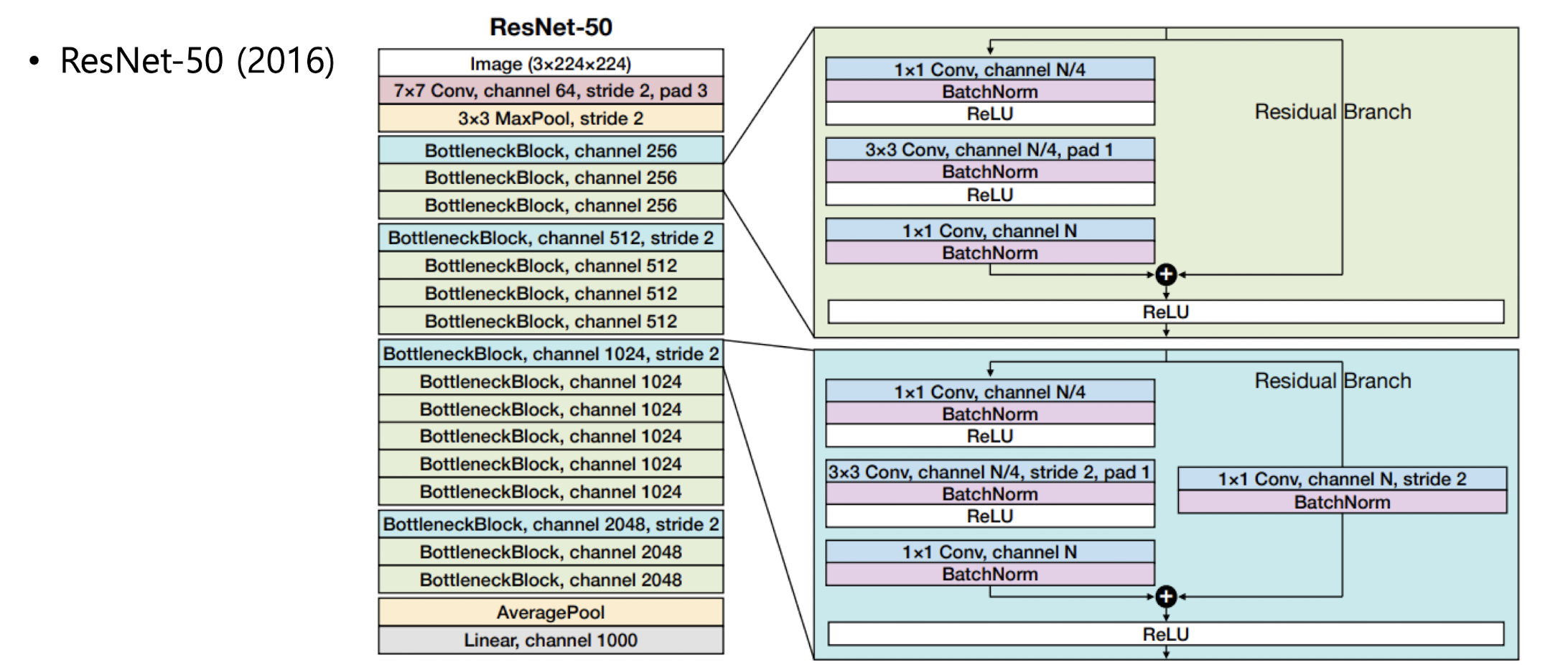
레이어가 50개
DenseNet
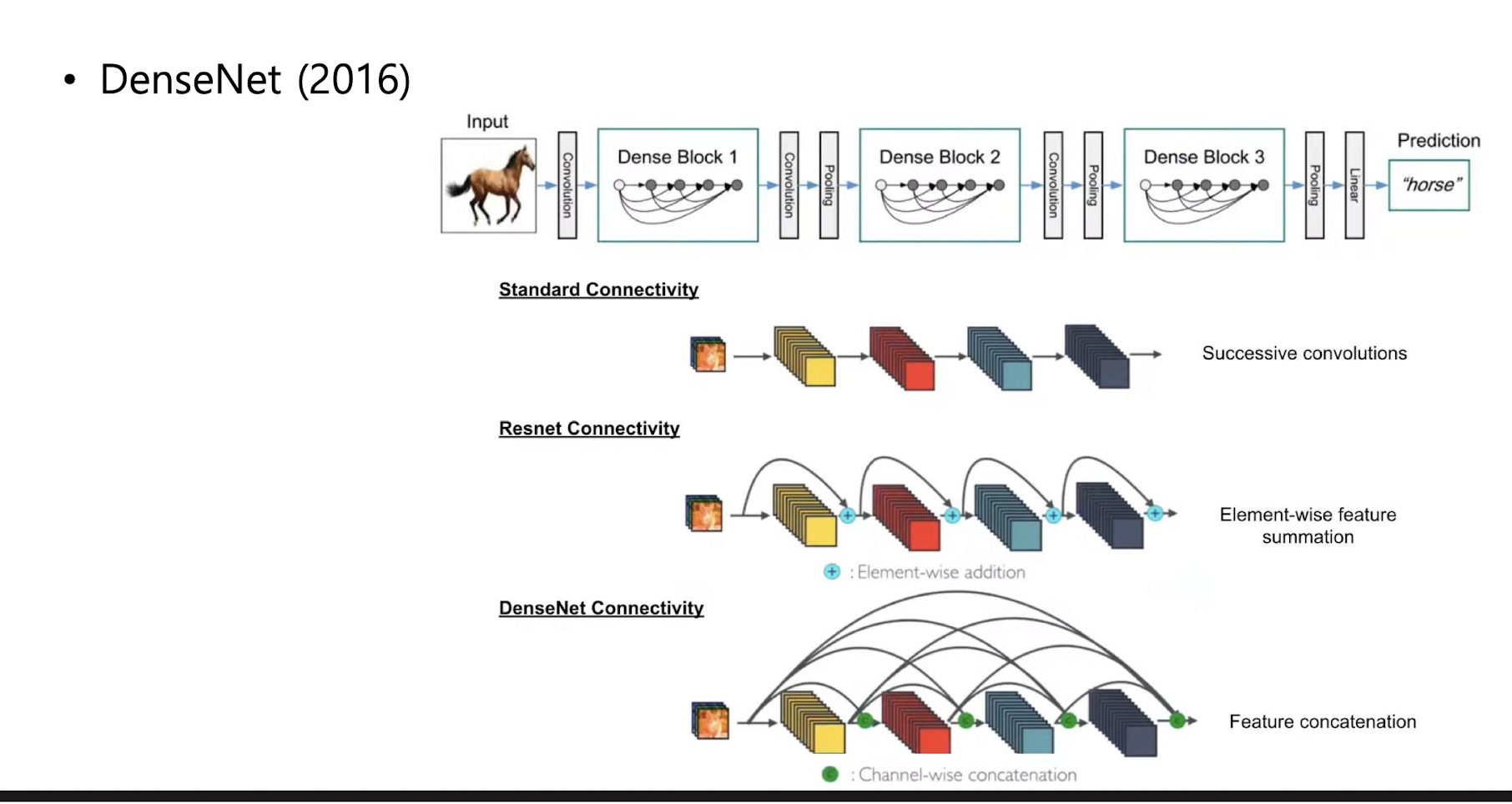
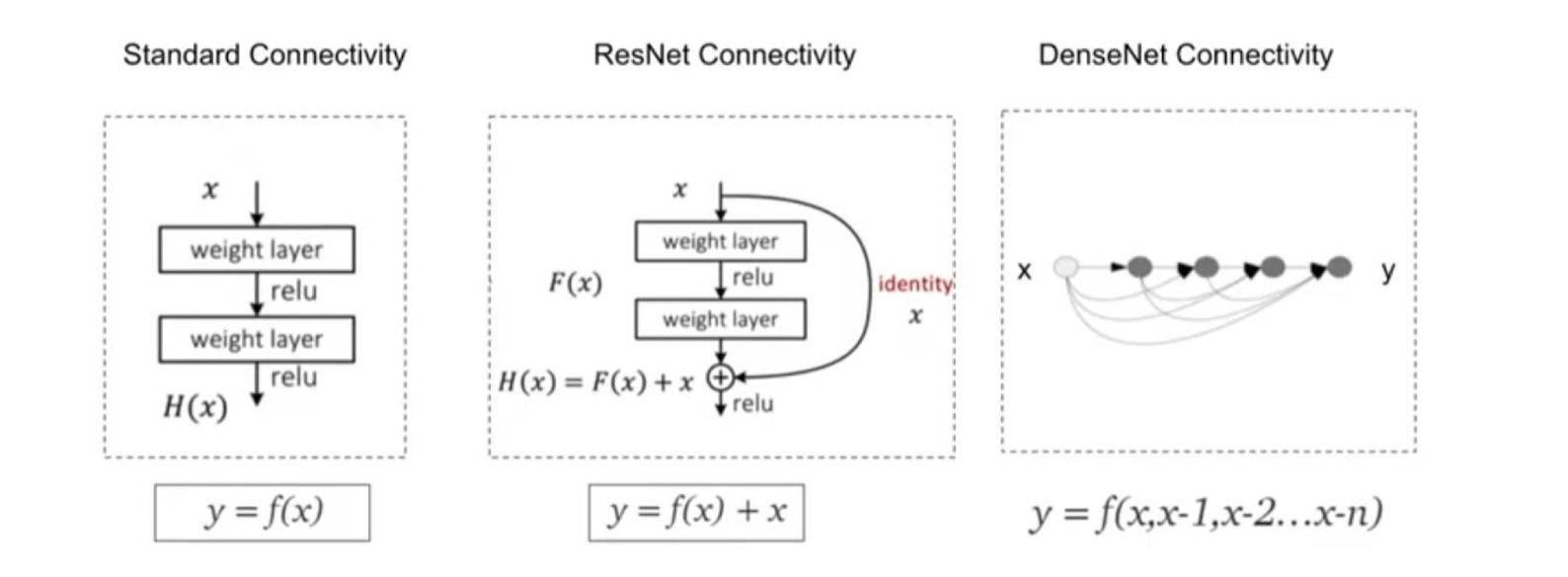
각 레이어가 앞선 모든 레이어의 출력을 입력으로 받는 형태(feature reuse)
기울기 소실 문제를 효과적으로 방지할 수 있다.
각 레이어는 적은 수의 필터만 추가로 학습하면 된다. 따라서 적은 수의 파라미터로 효율적인 성능
Deeper and deeper
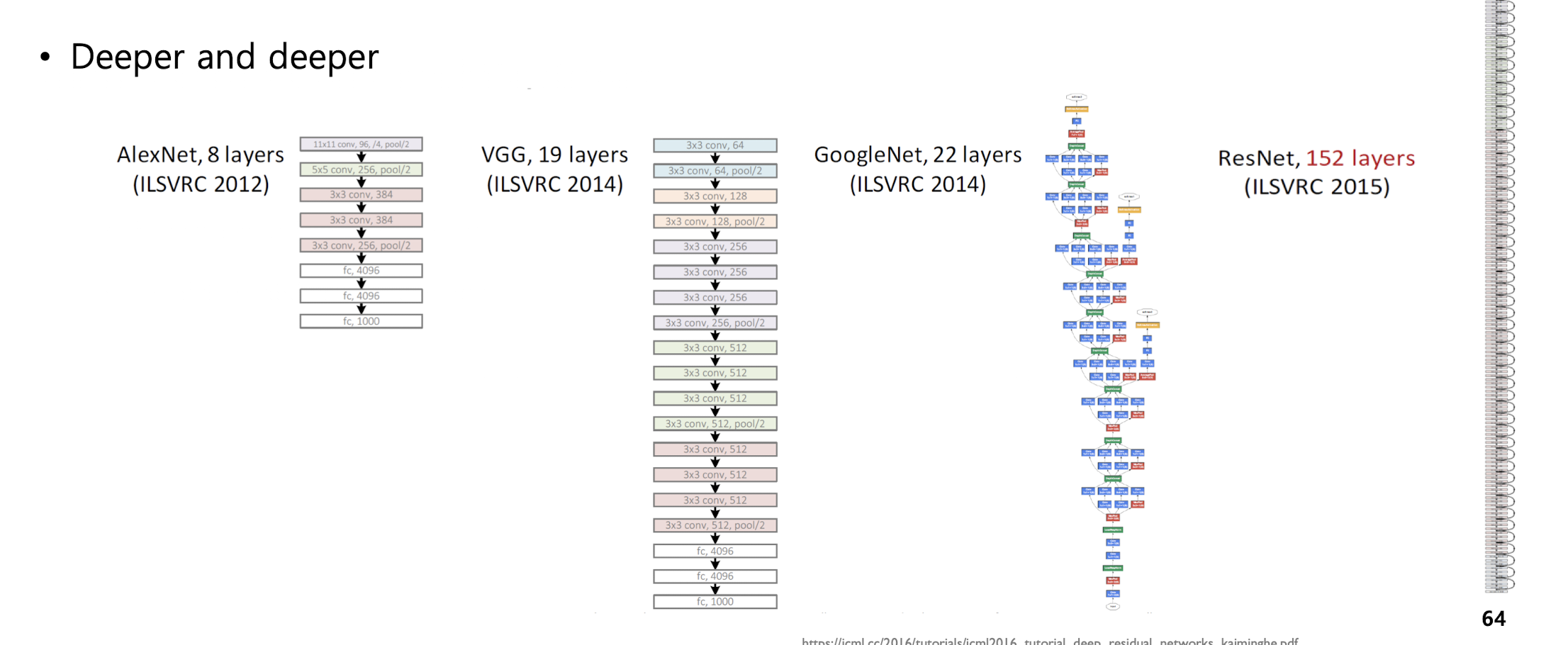
네트워크 구조들은 점점 더 깊어진다.
Object detection
bounding box (중심, 가로 세로) 문제 해결
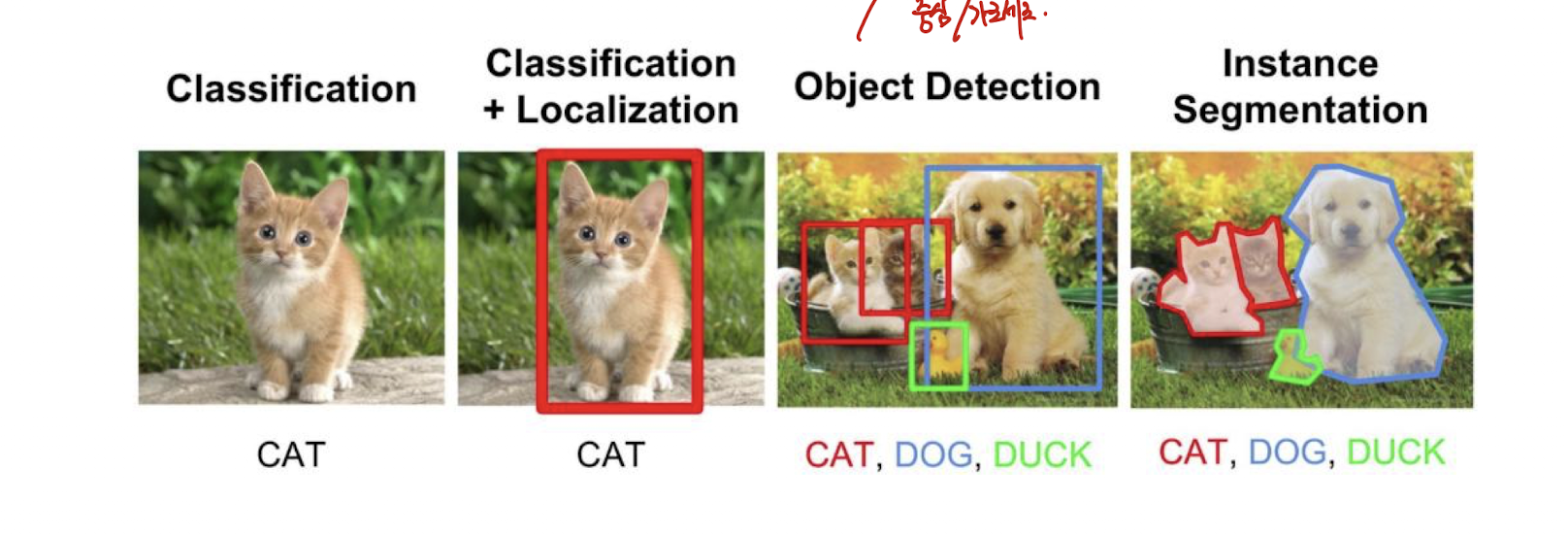
해당 문제들 해결하기 위해 다음과 같은 모델들이 제시됨.
R-CNN
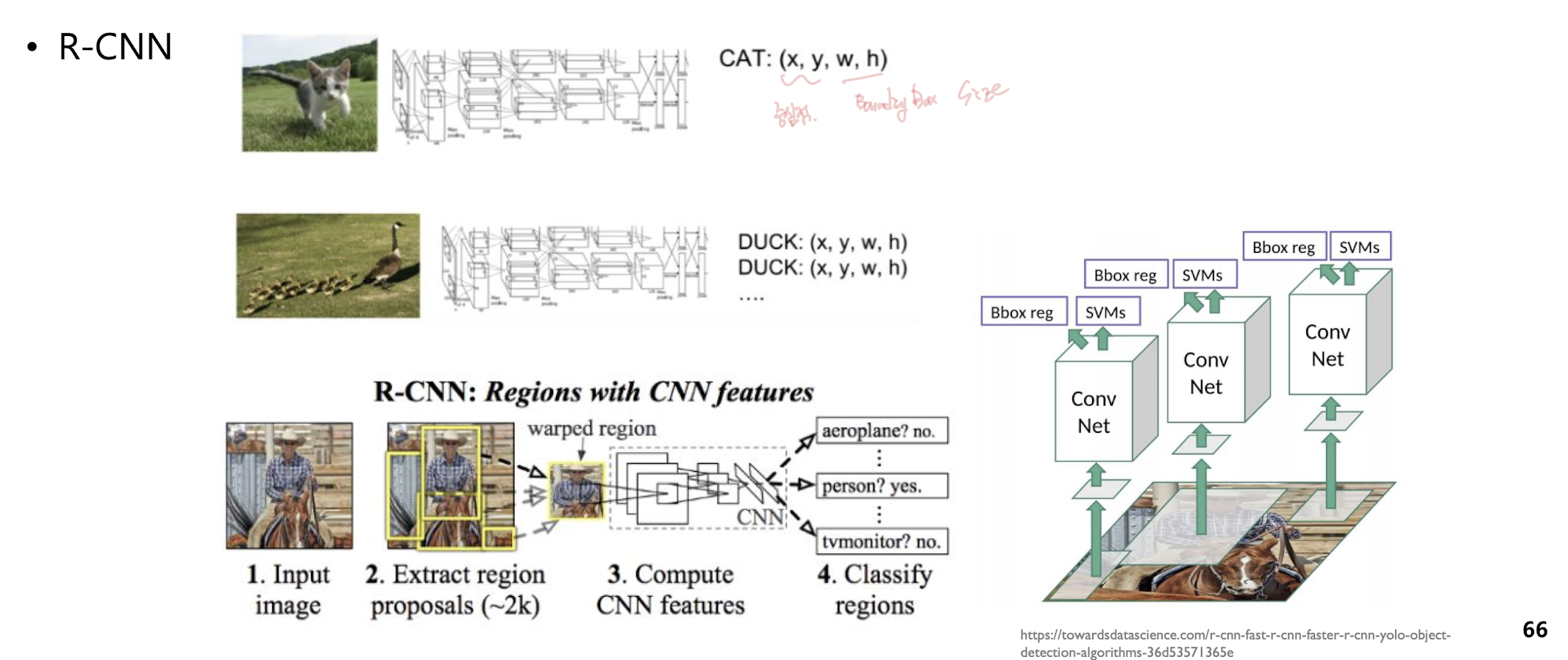
초기 모델
중심점의 좌표, 바운딩 박스의 사이즈 4개의 값을 찾아줌
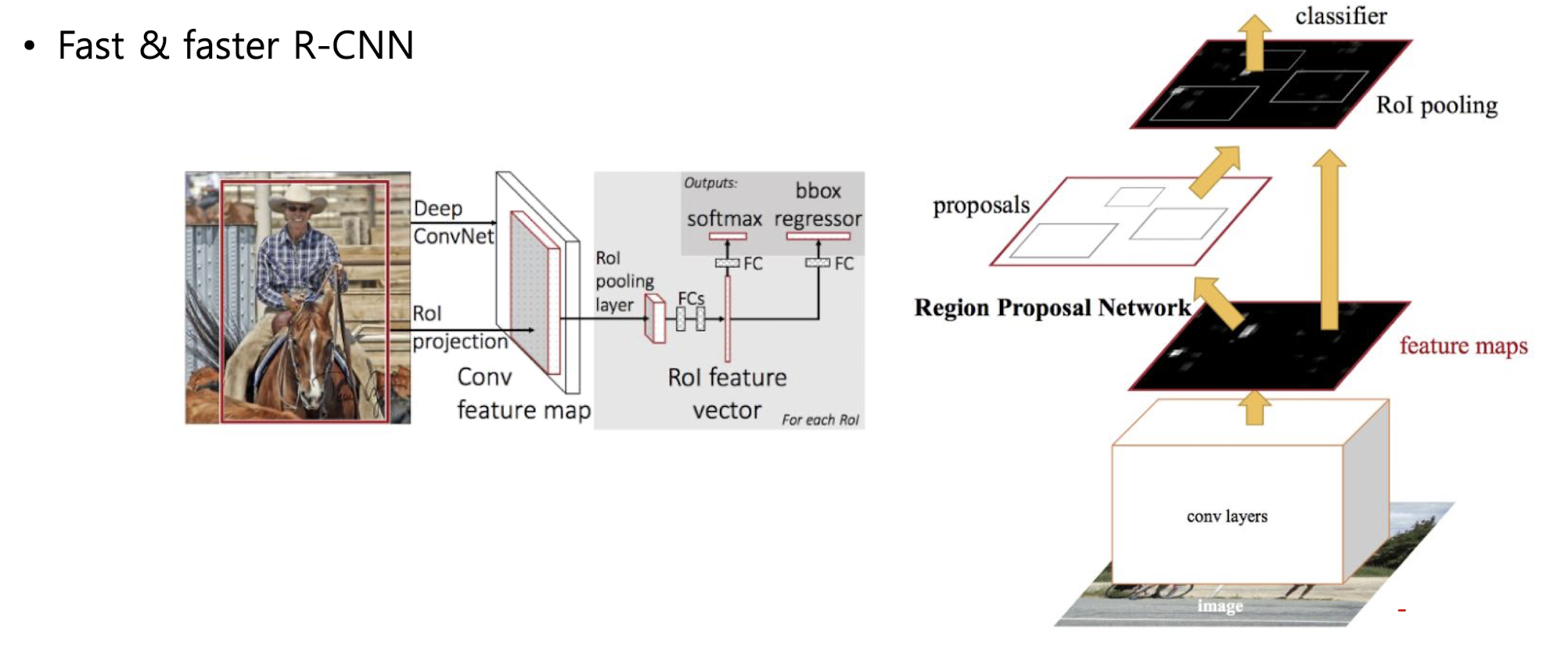
Fast&faster R-CNN
YOLO
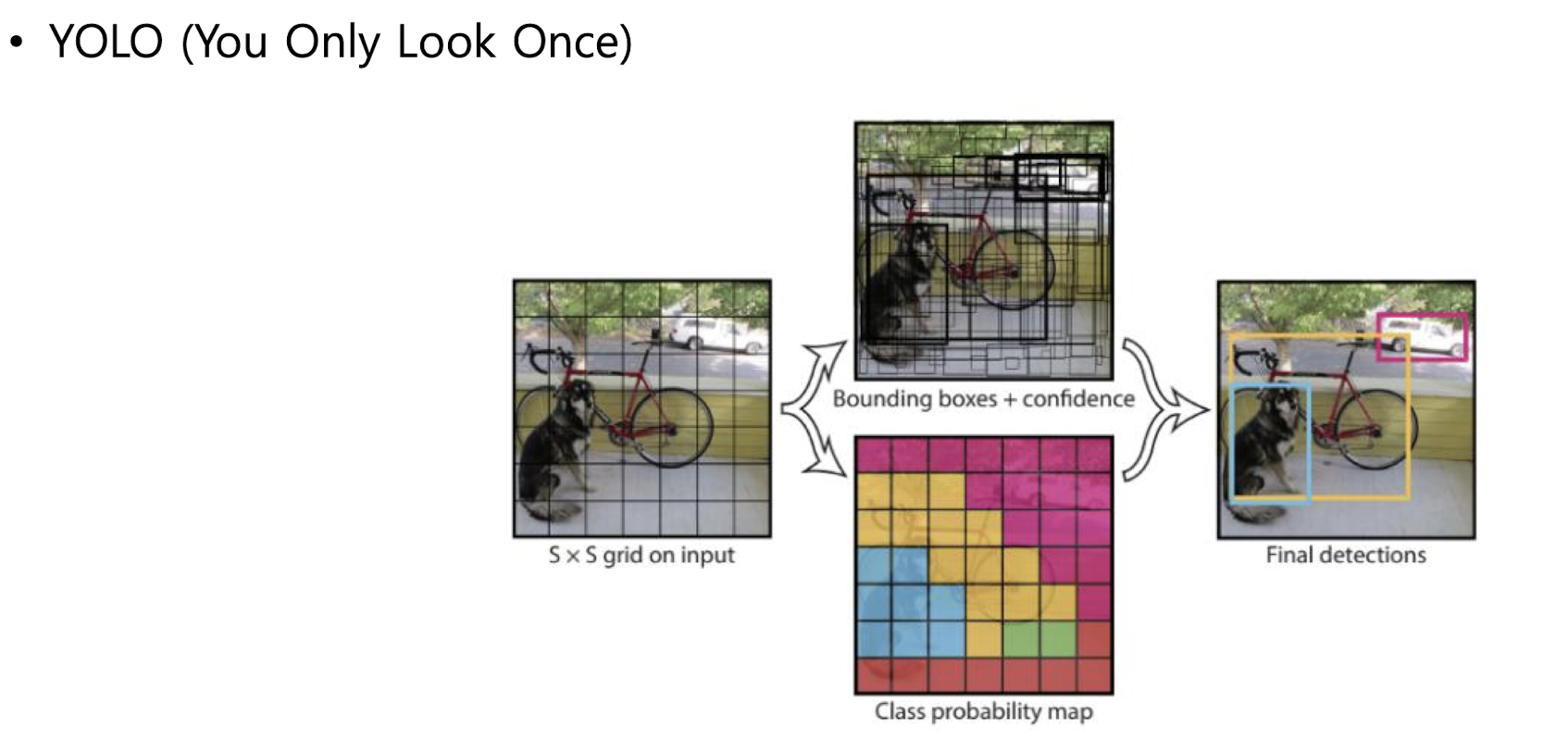
you only look once
앞에서는 기본적으로 2 step
1. 영역 찾고
2. 컨볼루션 레이어 통과해서 어떤 클래스에 속하는지 찾기
YOLO는 한번에 해결 -> 성능보다는 속도!
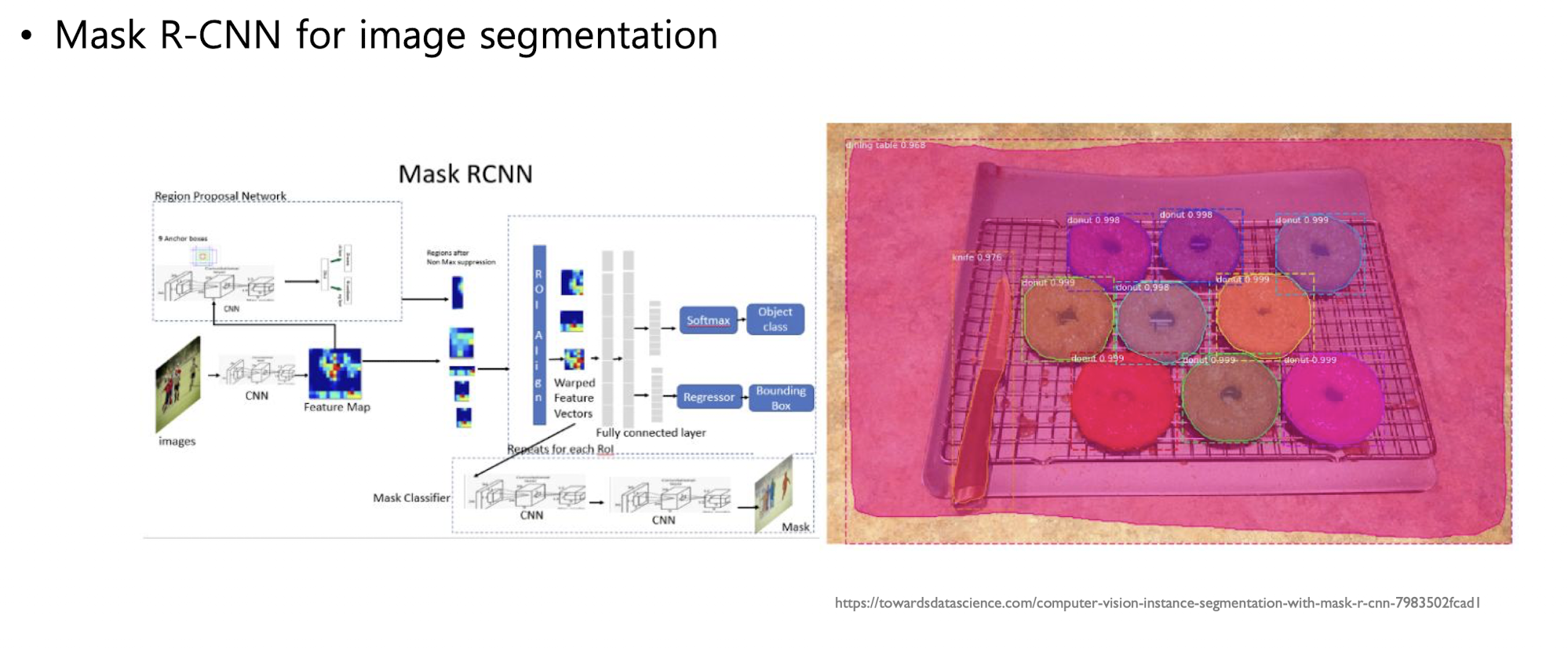
Mask R-CNN for image segmentaion