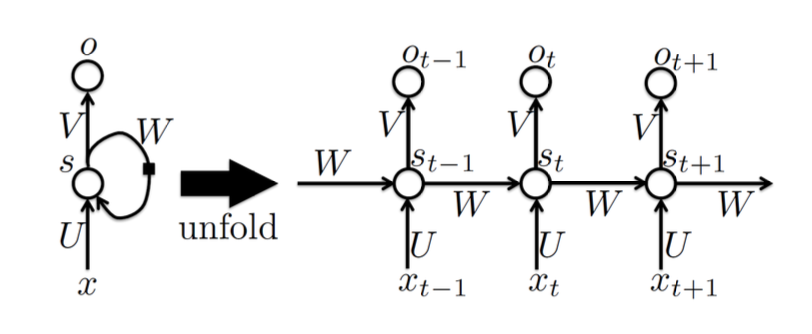
RNN? Recurrent neural networks : 순환 신경망. 순차적 데이터를 처리하기 위한 신경망 게열. 값의 시퀸스 x1 x2 x3 ... xt 같이 시퀀셜한 값을 처리하는데 특화된 신경망. 더 긴 시퀸스로 확장 가능 (문장, 음성, 시계열 데이터 ..)

Recurrent Neural Networks

---

Unfolding computational graphs

recursive, recurrent 계산을 반복적인 구조를 가진 게산 그래프로 펼치는 과정. 이때 동일한 파라미터 세타가 여러 시점에 걸처 공유됨.

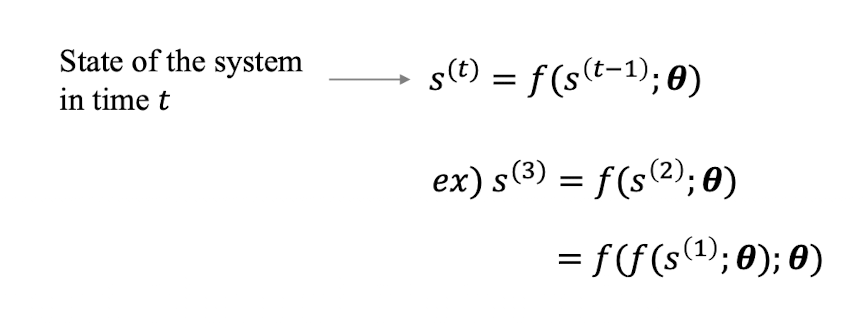
• 동적 시스템이란, 시간이 지남에 따라 상태가 변화하는 시스템. 외부신호 x(t)가 들어오면 시스템의 상태 s(t)는 다음과 같이 정의된다.
  

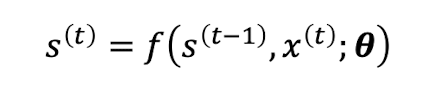
• s(t-1)은 이전 시점의 상태, x(t)는 현재 시점에 들어온 입력(외부 신호), theta는 f의 파라미터

• 해당 구조로 인하여 현재 상태 s(t)는 과거 모든 입력 정보를 일정 부분 포함하게 된다.

• 대부분의 RNN은 hidden unit h 사용

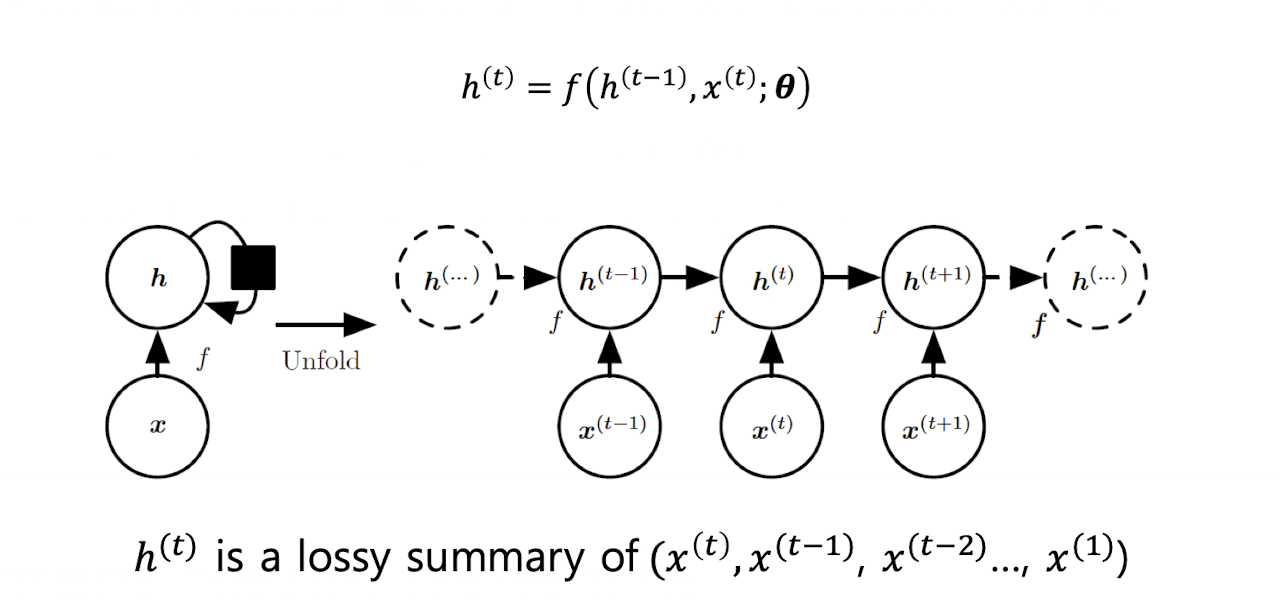
• 이전 히든 상태와 현재 입력을 함수에 넣어 새로운 히든 상태를 만든다.

• h(t)는 이전 입력값 x(t), x(t-1) ... 의 손실 있는 sum, 요약
  

---

RNN features

• RNN의 주요 설계 패턴
• RNN은 각 time step마다 출력을 생성, hidden unit 사이의 recurrent한 연결이 있다.
• 순환 연결은 한 시점의 출력에서 다음 시점의 은닉 유닛으로만 연결. 은닉 상태끼리 직접 연결되는 것이 아니라 한 시점의 출력값이 다음 시점의 은닉 유닛의 입력으로 사용
• 전체 시퀸스에 대해 단일 출력을 생성. 은닉 유닛들 사이에 순환 연결이 있다.

1. pattern 1
   
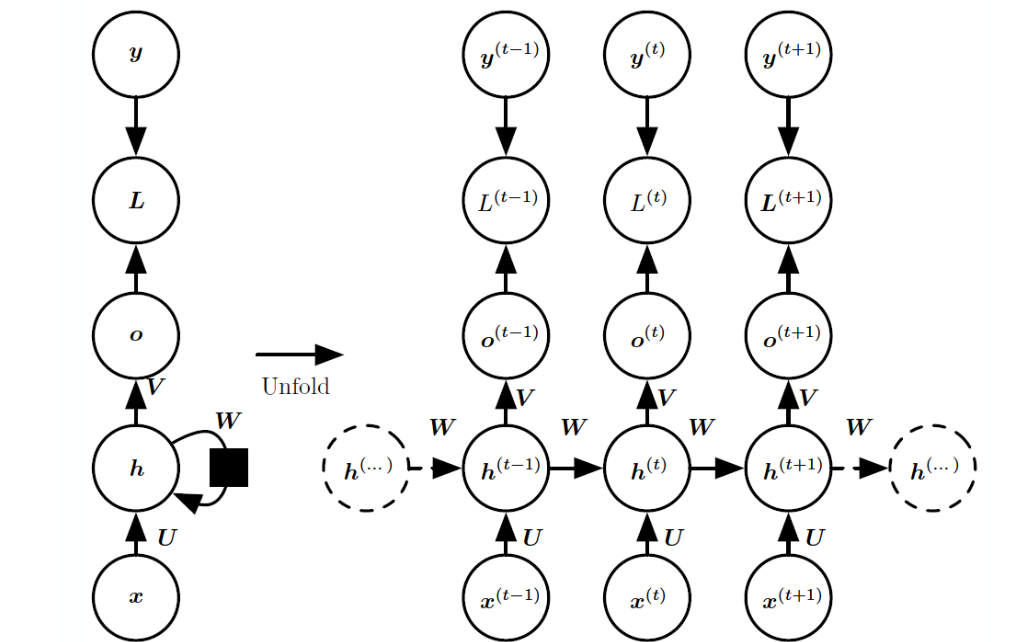
   y : 실제 정답, label
   o : output, 출력값
   L : loss, y와 o를 이용하여 계산
   h : hidden state, 이전 시점의 은닉 상태가 recurrent하게 연결
   x : 입력값

U : 입력->은닉
W : 은닉->은닉
V : 은닉->출력

오른쪽 그림과 같이 unfolding하게 되면 각 시점마다 같은 구조가 반복되고 이때 파라미터는 공유된다.
h끼리 직접 연결. 대표적인 RNN 구조이다.

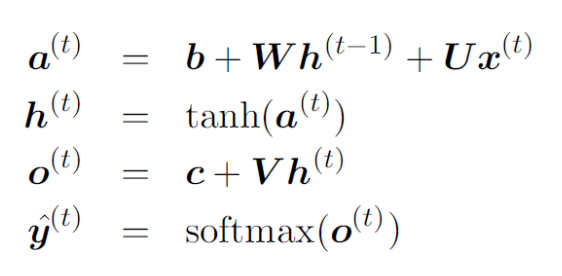
수식	설명
$a^{(t)} = b + W h^{(t-1)} + U x^{(t)}$	현재 시점의 은닉 상태를 계산하기 위한 선형 결합. 이전 은닉 상태, 현재 입력, 그리고 편향이 더해집니다.
$h^{(t)} = \tanh(a^{(t)})$	위에서 구한 $a^{(t)}$에 비선형 활성화 함수(tanh)를 적용해 현재 은닉 상태를 만듭니다.
$o^{(t)} = c + V h^{(t)}$	은닉 상태에서 출력층으로 변환(선형 결합)하며, 편향이 더해집니다.
$\hat{y}^{(t)} = \text{softmax}(o^{(t)})$	최종 출력값 $o^{(t)}$에 소프트맥스 함수를 적용해 예측 확률을 만듭니다.

2. pattern 2
   
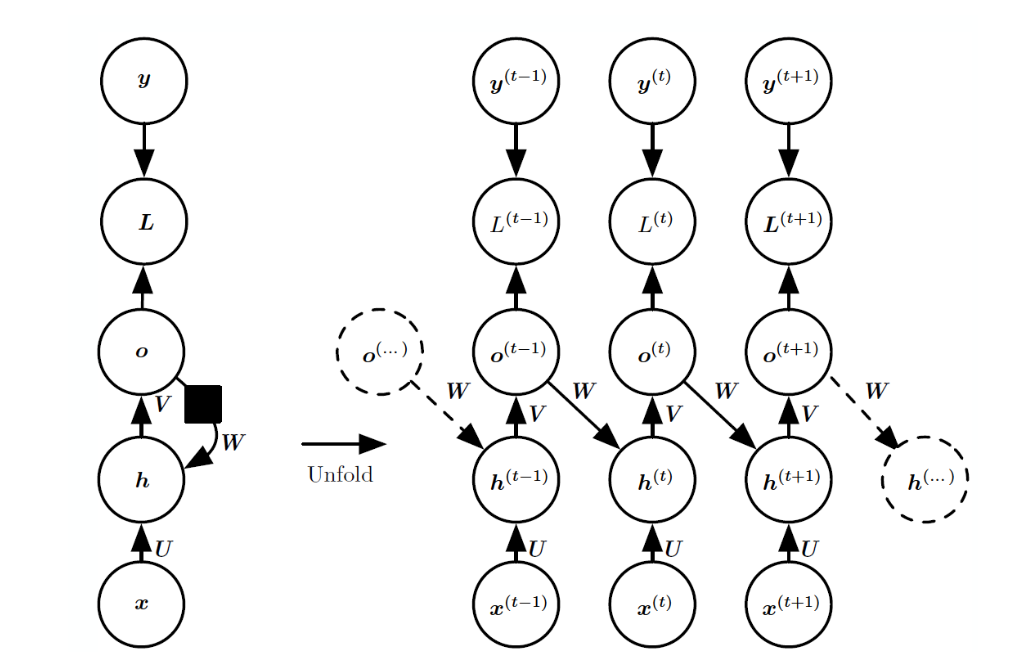
   위의 그림과 달리, 출력 o가 다음 시점의 h에 영향을 미친다.

3. pattern 3
   
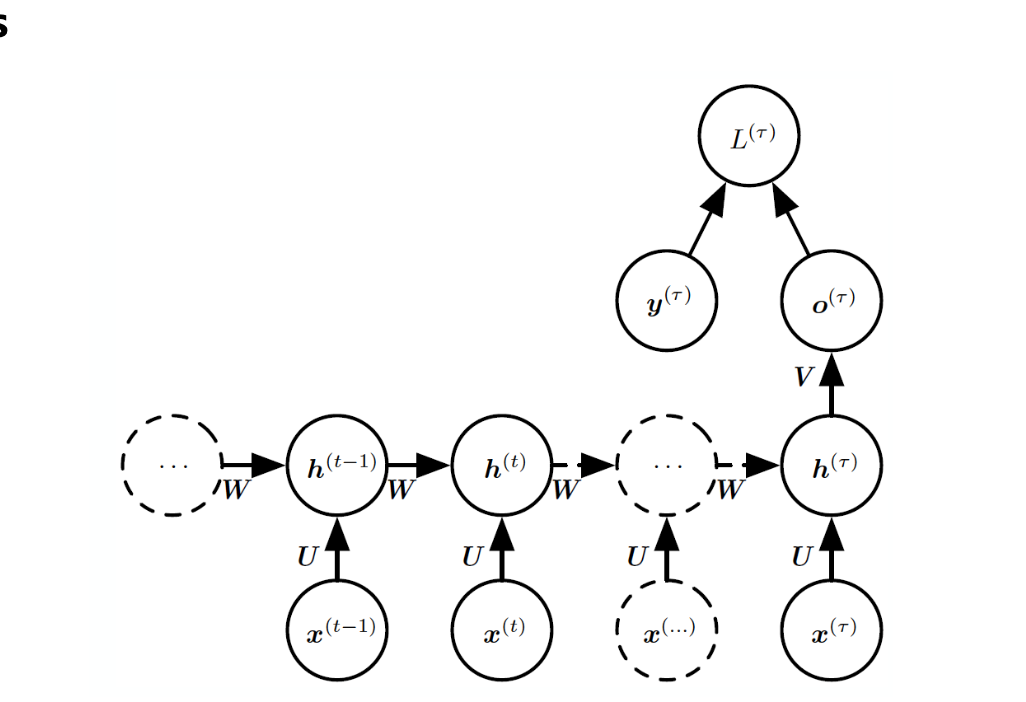
   입력 시퀸스 전체를 처리한 뒤, 마지막 은닉 상태에서만 출력

Computing the gradient

Backpropagation : 손실이 모든 시점에 전달되고, 계산량이 많다.

• 시퀸스의 각 시점마다 출력이 있고, 손실이 정의되어 있기 때문에 전체 손실은 모든 시점의 손실의 합산한 값이 된다. 해당 손실 정보다 모든 시점에 걸쳐 역전파되어 각 파라미터가 시퀸스 전체에 어떻게 영향을 미쳤는지 학습.
• 따라서 시퀸스 길이만큼 계산하여야 한다.

Backpropagation through time (BPTT)

RNN을 학습할 때 사용하는 표준 알고리즘. 기존의 역전파 알고리즘을 unfold된 RNN에 그대로 적용하면 된다.

• 현재 시점 $t$에서의 은닉 상태를 만들기 위한 선형 결합이다.
• $h^{(t-1)}$: 이전 시점의 은닉 상태
• $x^{(t)}$: 현재 입력
• $W$: 은닉 상태에서 은닉 상태로 가는 가중치
• $U$: 입력에서 은닉 상태로 가는 가중치
• $b$: 은닉 상태의 편향

---

은닉 상태에 비선형성 적용

• 위에서 계산한 $a^{(t)}$에 하이퍼볼릭 탄젠트(tanh)라는 비선형 활성화 함수를 적용해, 현재 시점의 은닉 상태 $h^{(t)}$를 만든다.
• 이 과정을 통해 신경망이 더 복잡한 패턴을 학습할 수 있다.

---

출력 계산

• 현재 시점의 은닉 상태 $h^{(t)}$를 출력값 $o^{(t)}$로 변환한다.
• $V$: 은닉 상태에서 출력으로 가는 가중치
• $c$: 출력의 편향

---

소프트맥스 함수로 확률 예측

• 출력값 $o^{(t)}$에 소프트맥스 함수를 적용해, 각 클래스에 대한 예측 확률을 만든다.
• 이 확률을 통해 모델이 각 클래스 중 어떤 것이 정답일지 예측한다.

---

전체 시퀀스에 대한 손실 함수

• 전체 시퀀스(여러 시점)에 대한 총 손실은, 각 시점별 손실 $L^{(t)}$을 모두 더한 값이다.
• 즉, 시퀀스의 모든 시점에서 예측이 얼마나 잘 되었는지 합산한다.

---

Cross-Entropy(교차 엔트로피) 손실

$p_{\text{model}}\left(y^{(t)} \mid \{x^{(1)}, \ldots, x^{(t)}\}\right)$ : 모델이 시점 t에서 실제 정답 yt일 확률을 예측한 값.
즉, 각 시점 t마다 정답일 예측값을 구하고, 해당 확률에 로그 값을 취함. 음수를 붙여 손실로 만들고 모든 t에 대해 합산

• Bar 기호는 조건부 확률의 기호이다. 입력 시퀸스 x1 ... xt가 주어졌을 때 정답 yt일 확률
• 각 시점 $t$에서, 모델이 실제 정답 $y^{(t)}$에 대해 예측한 확률의 로그 값을 취해 음수로 바꾼 뒤, 모든 시점에 대해 합산한다.
• 이 값이 작을수록(즉, 모델이 정답에 높은 확률을 줄수록) 모델이 잘 맞췄다는 의미다.
• Cross-Entropy 손실은 분류 문제에서 가장 널리 쓰이며, RNN의 각 시점에서 예측이 잘 되었는지를 평가하는 기준이다.

---

손실의 각 시점에 대한 미분

• 전체 손실 $L$은 모든 시점의 손실 $L^{(t)}$의 합이므로, 각 시점의 손실로 미분하면 1이 된다.

why?

전체 손실의 정의
전체 손실은 각 시점의 손실을 모두 더한 것이다.

예를 들어,

라고 하자.
이때 $L$을 $L^{(2)}$로 미분한다는 건, $L^{(2)}$가 1만큼 변할 때 $L$도 1만큼 변한다는 뜻이다.

왜냐하면,

• $L$에서 $L^{(2)}$는 1배로 더해져 있고

• $L^{(1)}, L^{(3)}$는 $L^{(2)}$와 상관없는 상수이기 때문에

• $L^{(2)}$로 미분하면 $L^{(2)}$만 1이 남고, 나머지는 0이 된다.

  $\frac{\partial}{\partial L^{(2)}} (L^{(1)} + L^{(2)} + L^{(3)}) = 0 + 1 + 0 = 1$

결론

• 전체 손실이 각 시점 손실의 “합”이기 때문에,
• $L$을 $L^{(t)}$로 미분하면 $L^{(t)}$만 1이 남고, 나머지는 0이 되어
• 결과적으로 $\frac{\partial L}{\partial L^{(t)}} = 1$이 된다.

---

출력 벡터에 대한 손실의 기울기

• $o^{(t)}$: 시점 $t$의 출력 벡터
• $\hat{y}_i^{(t)}$: 소프트맥스 결과, 클래스 $i$의 예측 확률
• $1_{i, y^{(t)}}$: 실제 정답이 $i$이면 1, 아니면 0 (원-핫 인코딩)
• 즉, 예측 확률에서 실제값(원-핫)을 뺀 값이 출력에 대한 손실의 기울기다.

---

은닉 상태에 대한 손실의 기울기 (마지막 시점)

• $h^{(\tau)}$: 마지막 시점 $\tau$의 은닉 상태
• $V$: 은닉 상태에서 출력으로 가는 가중치 행렬
• $\nabla_{o^{(\tau)}} L$: 출력에 대한 손실의 기울기
• 즉, 은닉 상태에 대한 손실의 기울기는 출력 기울기에 $V$의 전치 행렬을 곱해서 계산한다.

---

오른쪽: BPTT에서의 기울기(gradient) 계산 공식

• 은닉 상태 $h^{(t)}$에 대한 전체 손실 $L$의 기울기(gradient)는 다음과 같이 계산된다.
  $\nabla_{h^{(t)}} L = \left( \frac{\partial h^{(t+1)}}{\partial h^{(t)}} \right)^\top (\nabla_{h^{(t+1)}} L) + \left( \frac{\partial o^{(t)}}{\partial h^{(t)}} \right)^\top (\nabla_{o^{(t)}} L)$
• 이는 다시 아래와 같이 쓸 수 있다.
  $= W^\top (\nabla_{h^{(t+1)}} L) \ \mathrm{diag}\left(1 - (h^{(t+1)})^2\right) + V^\top (\nabla_{o^{(t)}} L)$
  • $W^\top$: 은닉 상태 간 가중치의 전치
  • $\mathrm{diag}(1 - (h^{(t+1)})^2)$: tanh 비선형성의 도함수(자코비안)
  • $V^\top$: 출력 가중치의 전치
  • $\nabla_{o^{(t)}} L$: 출력에 대한 손실의 기울기

---

bidirection RNN

과거와 미래의 정보 모두 활용
두 개의 RNN이 함께 동작한다. 하나는 입력 시퀸스를 정방향으로 처리하고, 다른 하나는 역방향으로 처리한다.
각 시점의 최종 은닉 상태는, 정방향과 역방향 은닉 상태를 합쳐서 계산.

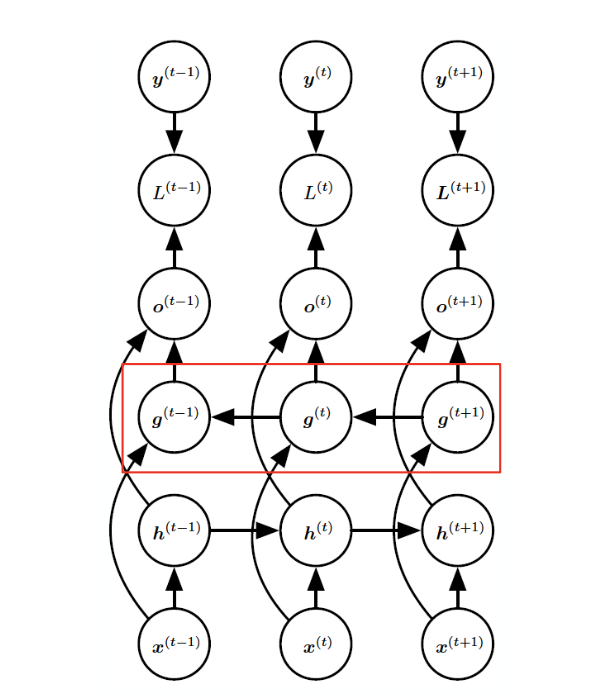
문맥 파악이 더 정확해진다는 장점이 있음.

---

Encoder-decoder seqence-to-seqence architectures

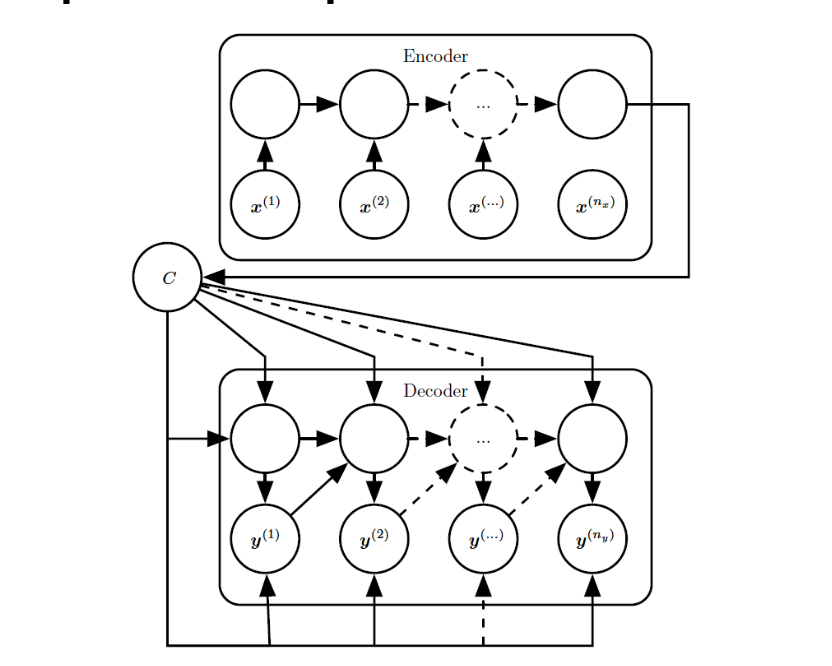
입력 시퀸스와 출력 시퀸스의 길이가 다를 수 있다. 번역, 질의응답 등 .. 이때 입력 시퀸스 전체의 의미를 context vector c에 담아 해당 벡터를 기반으로 출력 시퀸스를 생성하는 것이 seq2seq의 원리

입력 시퀸스 x를 인코더가 context vector c로 변환(RNN, LSTM 등 다양한 구조 사용)하여,
디코더는 c와 이전에 생성된 토큰들을 참고하여 다음 토큰을 예측한다.

---

Deep RNN

RNN은 입력 시퀸스를 처리할 때, 세 가지 주요한 transformation을 수행한다.
1. 입력 -> 은닉
2. 이전 은닉 -> 다음 은닉
3. 은닉 -> 출력

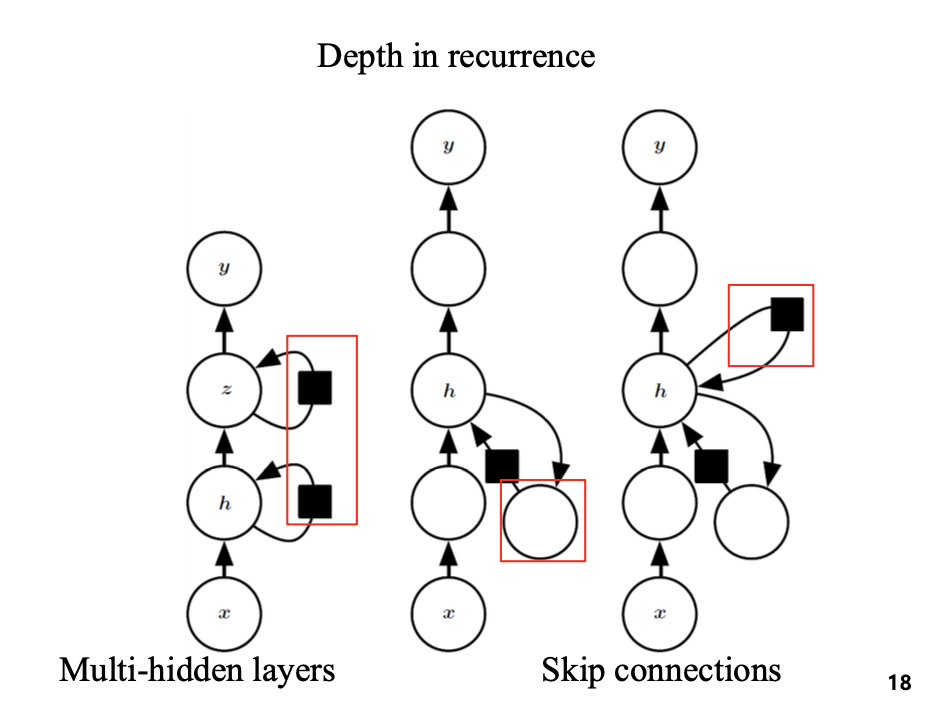
해당 그림처럼, 여러 은닉층을 쌓아 RNN의 깊이를 증가시킬 수 있다.
skip connection은 중간 층을 건너뛰는 연결 -> 학습 안정성과 성능 향상에 도움을 준다.

RNN examples

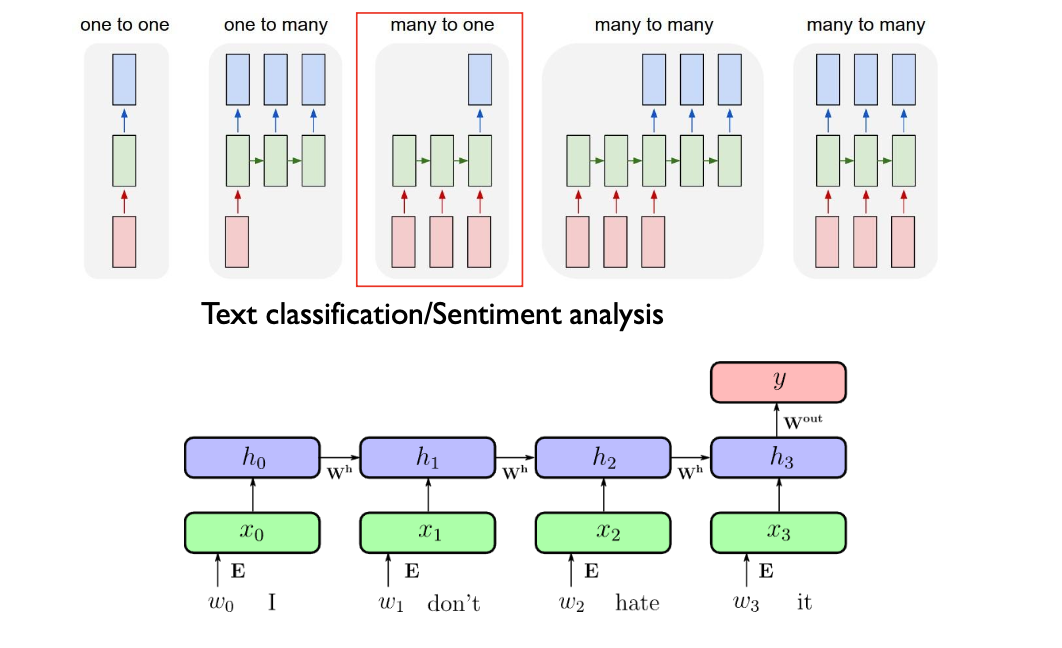
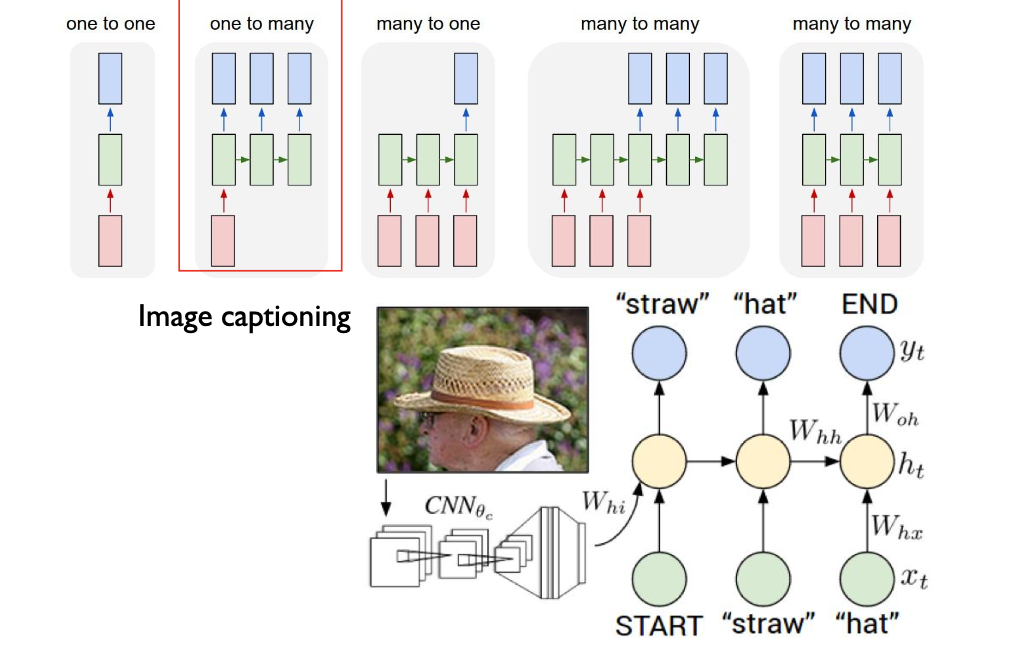
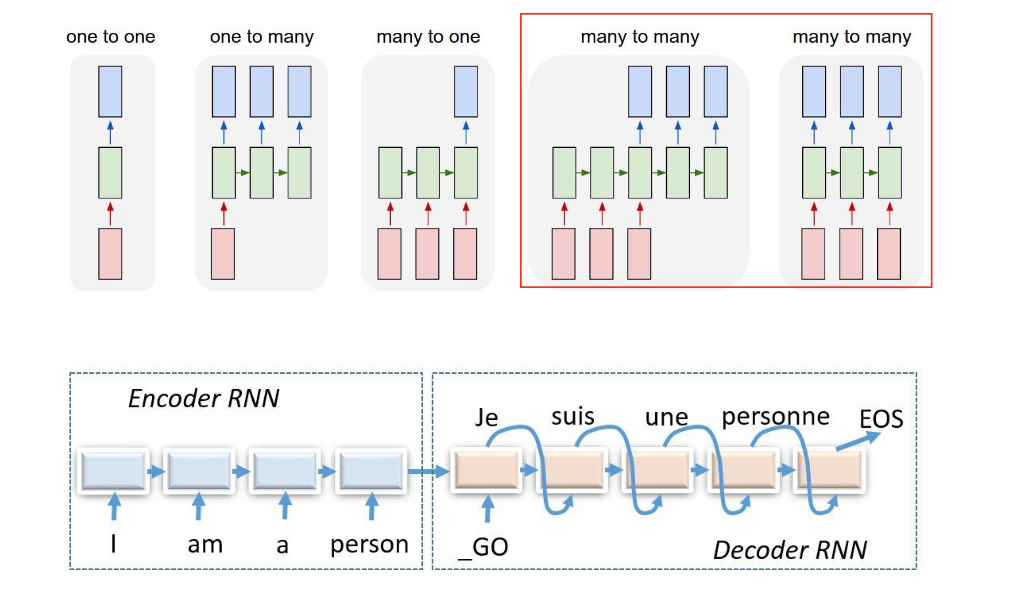
Long Short-Term Memory

장기 의존성. 가까이 있는 단어는 RNN도 관계를 잘 기억할 수 있지만, 멀리 있는 단어는 중요한 정보를 뒷부분까지 잘 전달하지 못함(기울기 소실)

LSTM

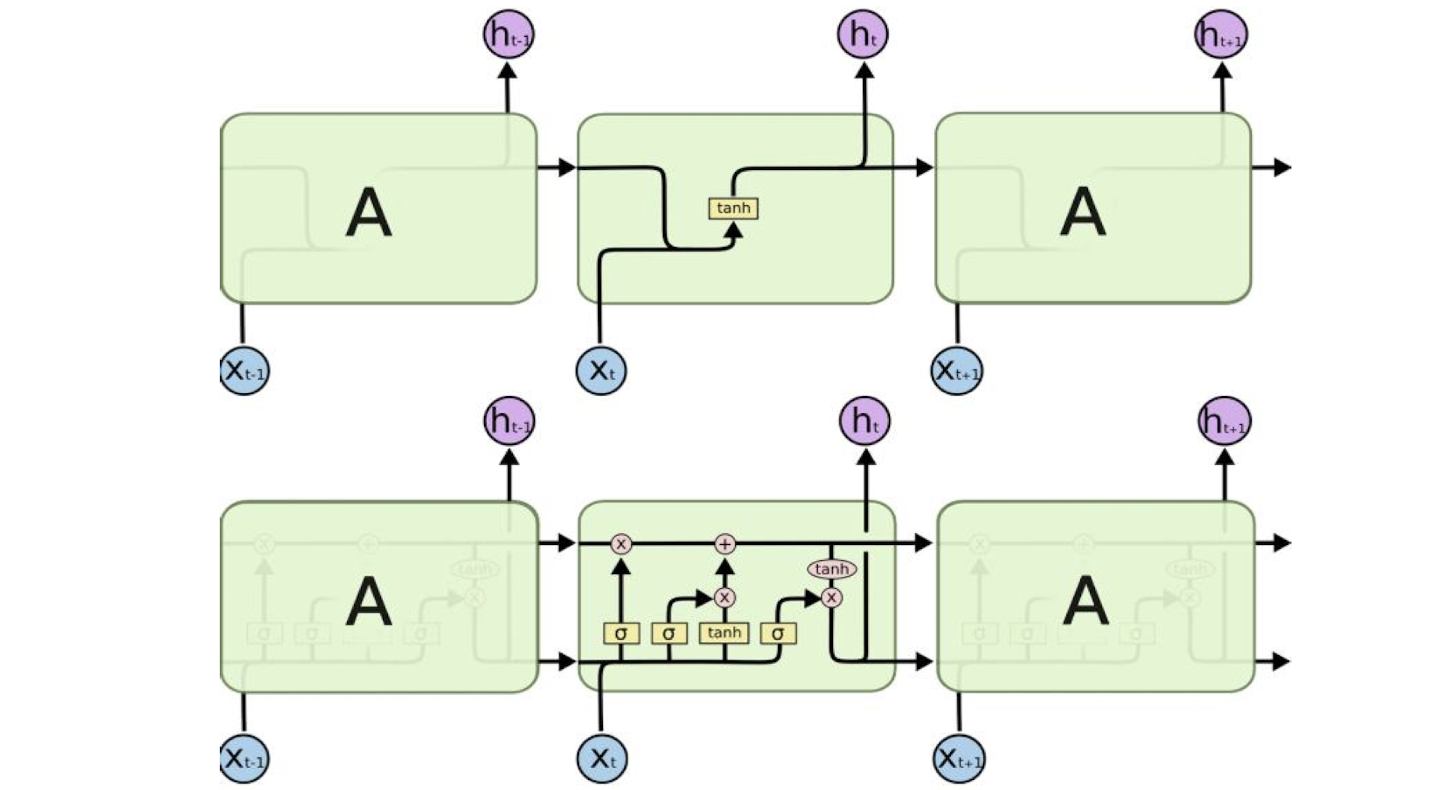
위 그림은 기본 RNN, 아래 그림은 LSTM

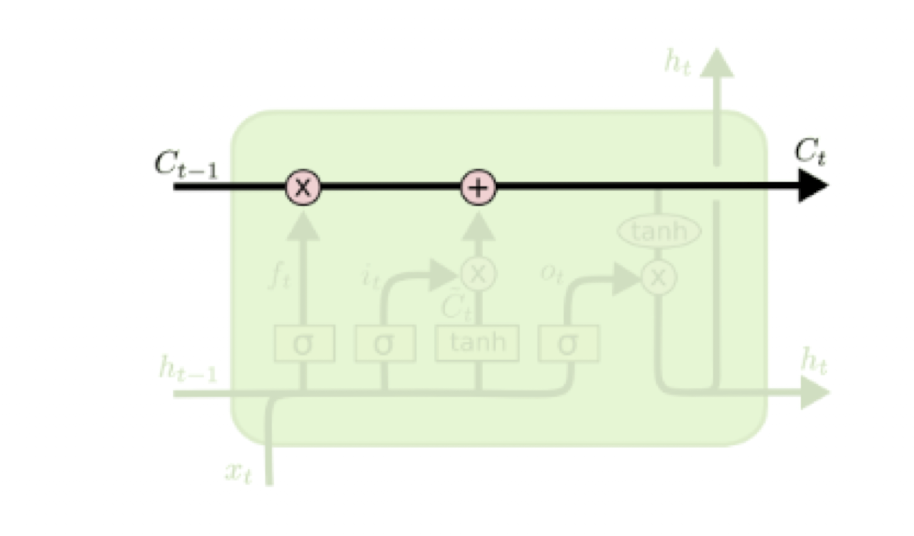
Cell state(가로로 뻗은 선)은 정보를 오랫동안 기억하고 전달하는 역할을 한다.
정보를 거의 변형하지 않고, 어떤 정보를 cell state에 남길지/지울지/추가할지 선택적으로 조절

Forget state

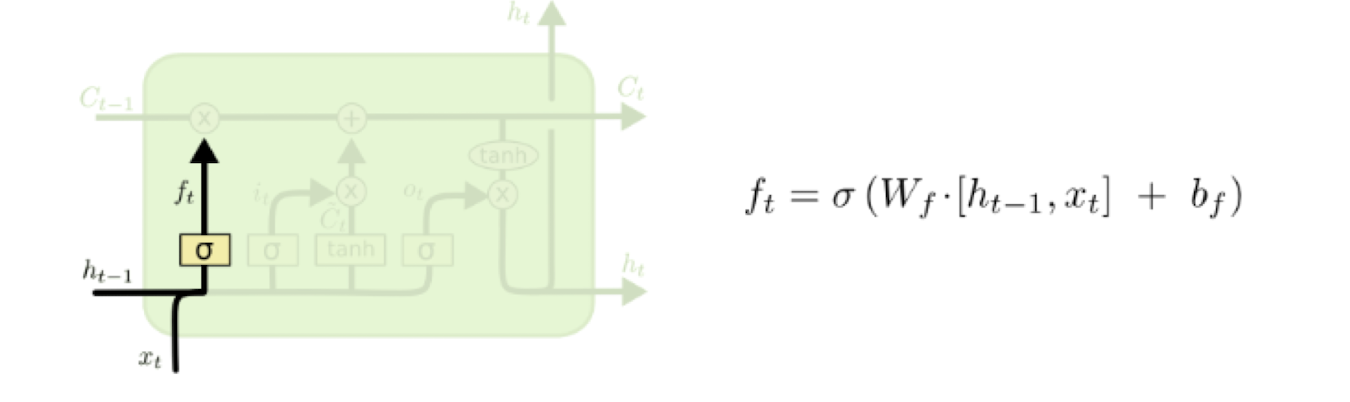
망각 게이트. 이전의 메모리를 얼마나 잊어야 하는가?
값이 1이면 완전히 기억
0이면 완전히 망각

Input gate and input

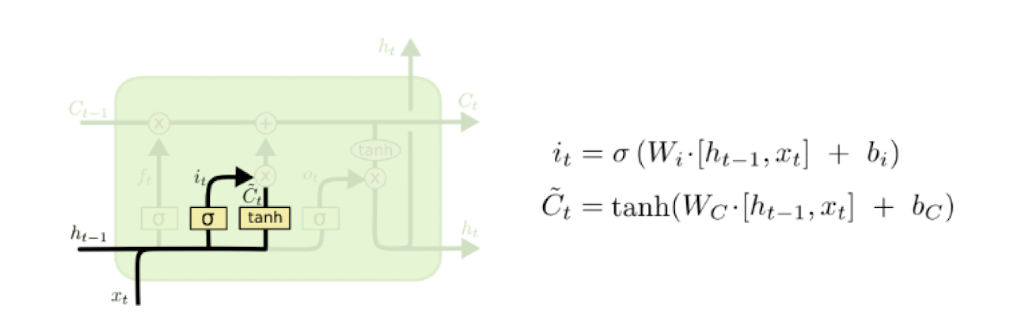
아까다정리했는데날라갔다

새로운 정보를 얼마나 넣을 것이냐

Combination of input and forget gate

입력게이트와 망각게이트의 조합은 셀 상태에 장기 기억을 저장한다.
이때 입력 게이트는 새로운 정보를 얼마나 더할지
망각 게이트는 기존 과거 정보를 얼마나 잊을지 결정

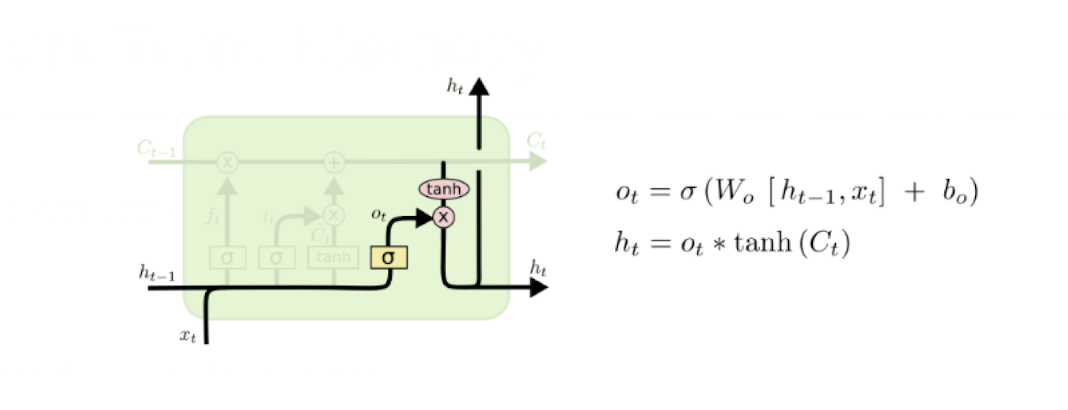
Output gate

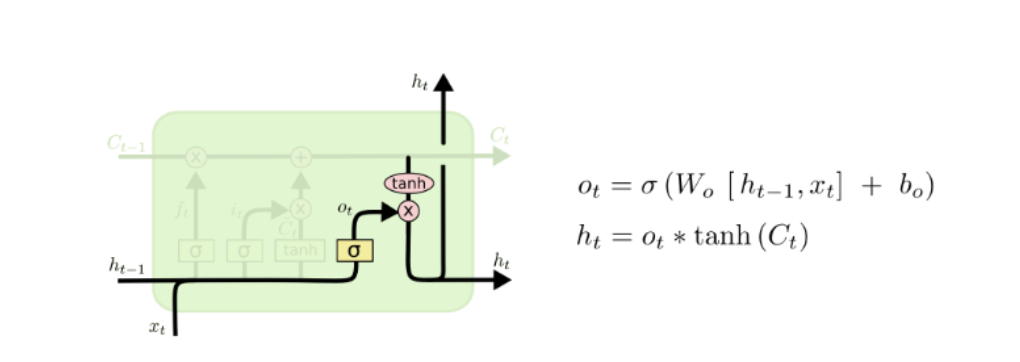
업데이트된 셀 상태가 은닉 노드로 전달됨.

수식 정리. 조금어려움

망각 게이트 (Forget Gate)

• $f_t$: 망각 게이트의 출력(0~1 사이 값)
• $\sigma$: 시그모이드 함수
• $W_f$: 망각 게이트의 가중치
• $[h_{t-1}, x_t]$: 이전 은닉 상태와 현재 입력의 결합
• $b_f$: 망각 게이트의 편향
• 역할: 이전 셀 상태 $C_{t-1}$에서 얼마나 정보를 유지할지 결정

---

입력 게이트 (Input Gate)

• $i_t$: 입력 게이트의 출력(0~1 사이 값)
• $W_i$: 입력 게이트의 가중치
• $b_i$: 입력 게이트의 편향
• 역할: 새로운 정보 $\tilde{C}_t$를 얼마나 셀 상태에 더할지 결정

---

셀 후보값 (Cell Candidate)

• $\tilde{C}_t$: 셀 상태에 추가될 새로운 후보값
• $W_C$: 셀 후보값 가중치
• $b_C$: 셀 후보값 편향
• $\tanh$: 하이퍼볼릭 탄젠트 함수(값의 범위를 -1~1로 제한)

---

셀 상태 업데이트 (Cell State Update)

• $C_t$: 현재 셀 상태
• $f_t * C_{t-1}$: 이전 셀 상태에서 남길 정보
• $i_t * \tilde{C}_t$: 새로 더할 정보

---

출력 게이트 (Output Gate)

• $o_t$: 출력 게이트의 출력(0~1 사이 값)
• $W_o$: 출력 게이트의 가중치
• $b_o$: 출력 게이트의 편향
• 역할: 셀 상태에서 어떤 정보를 은닉 상태로 보낼지 결정

---

은닉 상태(출력) 계산 (Hidden State / Output)

• $h_t$: 현재 시점의 은닉 상태(출력)
• $o_t$: 출력 게이트의 값
• $\tanh(C_t)$: 셀 상태의 비선형 변환

---

LSTM은 입력 게이트, 망각 게이트, 출력 게이트, 셀 상태를 조합해
긴 시퀀스에서도 중요한 정보를 효과적으로 기억하고 전달한다.

Attention

Attention 메커니즘은 인코더-디코더 RNN 구조에서 긴 문장 번역 등 입력 시퀸스와 출력 시퀸스 사이의 거리가 멀어질수록 입력 정보가 출력에서 사라지는 문제를 해결하기 위해 고안

기존 Encoder-Decoder RNN 구조에서는 입력 시퀸스 전체 정보를 하나의 고정된 context vector에 압축하여 디코더로 전달. 입력 시퀸스가 길어질수록 context vector에 모든 정보를 담기 어렵고, 정보 소실이 일어날 수 있다.

Attention은 디코더가 각 출력시점마다 인코더의 모든 은닉상태를 참조할수있게 한다.
-> 인코더의 은닉 상태들 중 현재 디코더 은닉 벡터와 관련있는 인코더 은넥 벡터에 더 많은 가중치를 줌. (attention weight)
-> 해당 가중치들을 이용하여, 가중 합을 만듦

직접적으로 Long Term Dependency를 해결. 어디에 집중해야 하는지 직접 계산함.

유사한 hidden vector를 더 많이 출력해라.

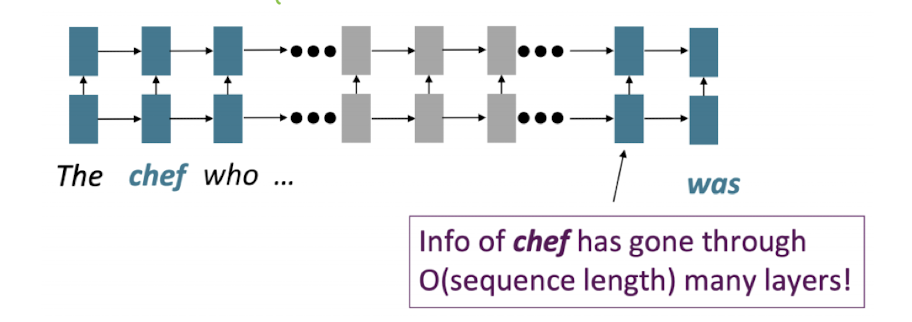
이렇게 chef와 was 거리 사이가 멀면 정보가 소실되거나 약해질 수 있음.

---

example

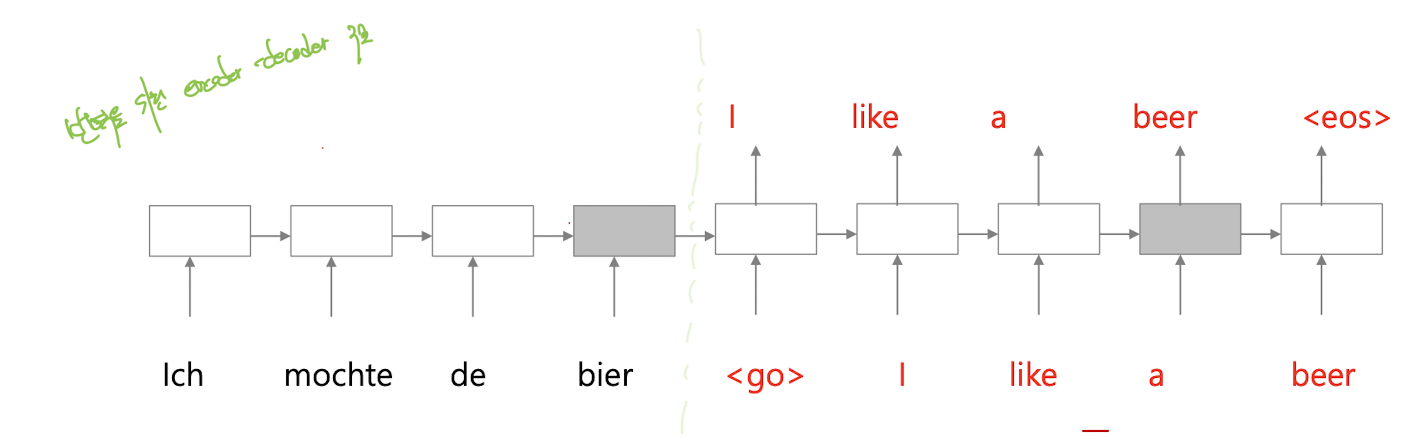
만약 인코더에서 bier에 해당하는 은닉 벡터가 디코더에서 beer을 예측할 때의 은닉 벡터와 비슷하다면, 그것을 디코딩에 활용할 수 있다.

Prediction without attention

• $s_t$: 디코더의 현재 은닉 상태
• $s_{t-1}$: 이전 디코더 은닉 상태
• $y_{t-1}$: 이전에 생성된 출력(토큰)
• $f$: 디코더의 상태 갱신 함수(RNN, LSTM 등)
  • 디코더는 오직 이전 상태와 이전 출력만 참고하여 현재 상태를 계산한다.
  • 인코더 전체 정보를 하나의 context vector로만 요약해서 사용한다.

Prediction with attention

• $c_t$: 어텐션에 의해 계산된 context vector (현재 시점 $t$에서 입력 시퀀스 전체의 정보를 가중합으로 요약)
  • 디코더는 이전 상태, 이전 출력뿐 아니라, 인코더의 모든 은닉 상태를 참고해 만든 $c_t$를 추가로 입력받는다.
  • $c_t$는 인코더의 각 은닉 상태 $h_i$와 디코더의 현재 상태 $s_t$의 유사도(어텐션 가중치)를 곱해 합산해서 만든다.
  • 즉, 입력 시퀀스의 중요한 부분에 집중(attend)하여 더 정확한 예측이 가능하다.

• 아래쪽: "Ich möchte de bier" (독일어 입력 시퀀스, 인코더)
• 위쪽: "<\go> I like a beer" (영어 출력 시퀀스, 디코더)
• 어텐션이 적용될 때, 디코더가 "beer"를 예측할 때 인코더의 "bier" 은닉 상태에 더 집중하여 context vector $c_t$를 만든다. 뭔얘기냐? s1,s2,s3 .. 각 state에 각각 유사도를 계산한 후, 어디에 집중해야하는지를 계산하여 ct

---

step

1. Attention Score 계산 및 Softmax 정규화

• 각 인코더 hidden state $h_i$와 디코더 hidden state $s_t$의 유사도를 계산해 attention score $e_{t,i}$를 만든다.
• Softmax 함수를 적용해 모든 score의 합이 1이 되도록 정규화한다.
  $\alpha_{t,i} = \frac{\exp(e_{t,i})}{\sum_j \exp(e_{t,j})}$
  • $\alpha_{t,i}$: 각 인코더 hidden state에 대한 attention weight (attention distribution)
  • $\sum_i \alpha_{t,i} = 1$

2. Context Vector 계산

• 각 인코더 hidden state $h_i$에 attention weight $\alpha_{t,i}$를 곱해서, 모두 더해 context vector $c_t$를 만든다.
  $c_t = \sum_i \alpha_{t,i} h_i$

3. Context Vector와 Decoder Hidden State 결합

• 마지막 단계에서는 context vector $c_t$와 디코더의 현재 hidden state $s_t$를 결합(concatenate)한다.
  $a_t = \tanh(W_c [c_t; s_t])$
  • $[c_t; s_t]$: context vector와 decoder hidden state의 벡터 연결(concatenation)
  • $W_c$: 결합 후 projection을 위한 가중치 행렬
  • $a_t$: 최종적으로 다음 출력(예측)에 사용될 attention vector

4. 출력층에 전달

• 이 attention vector $a_t$는 softmax 등 출력층에 전달되어, 최종 예측(다음 단어 등)에 활용된다.

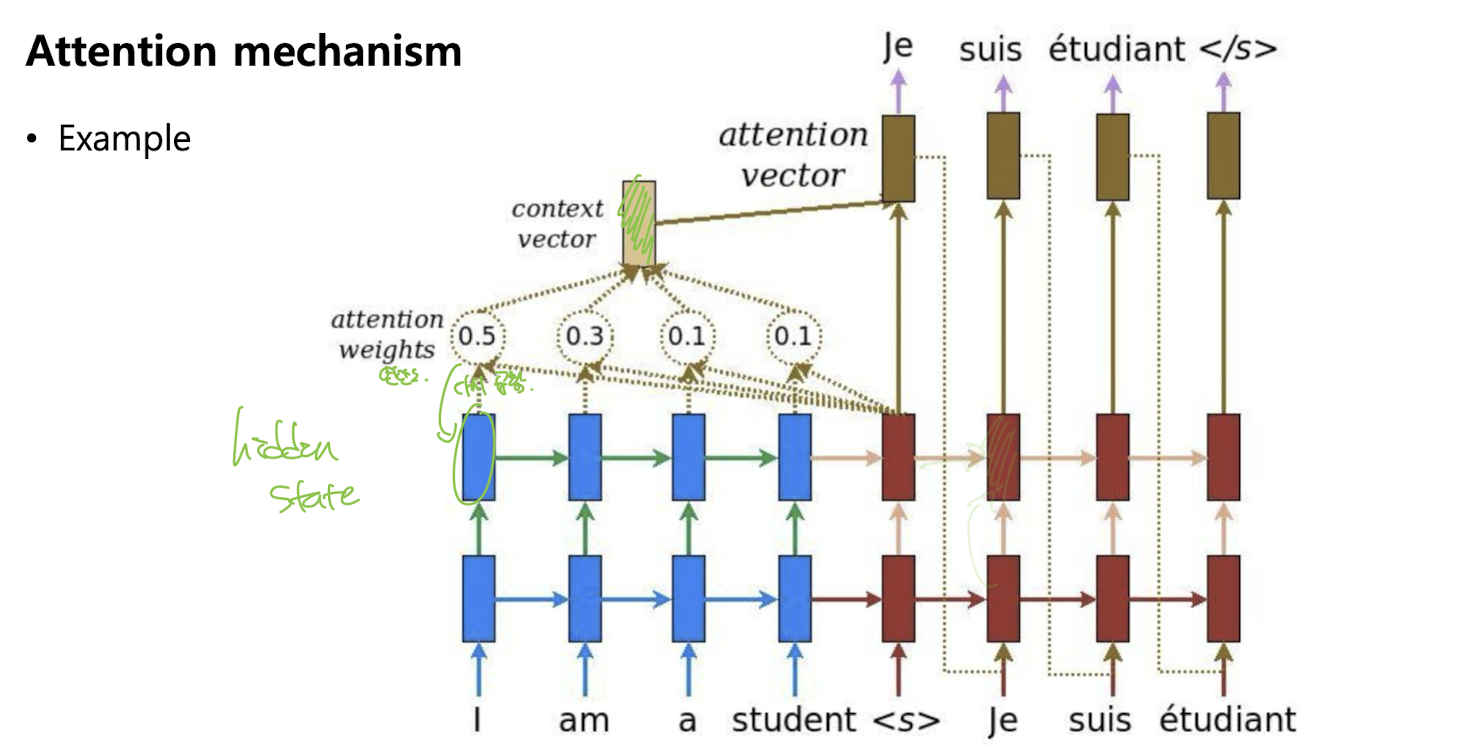
그림 보면 이해 잘됨

---

Score function

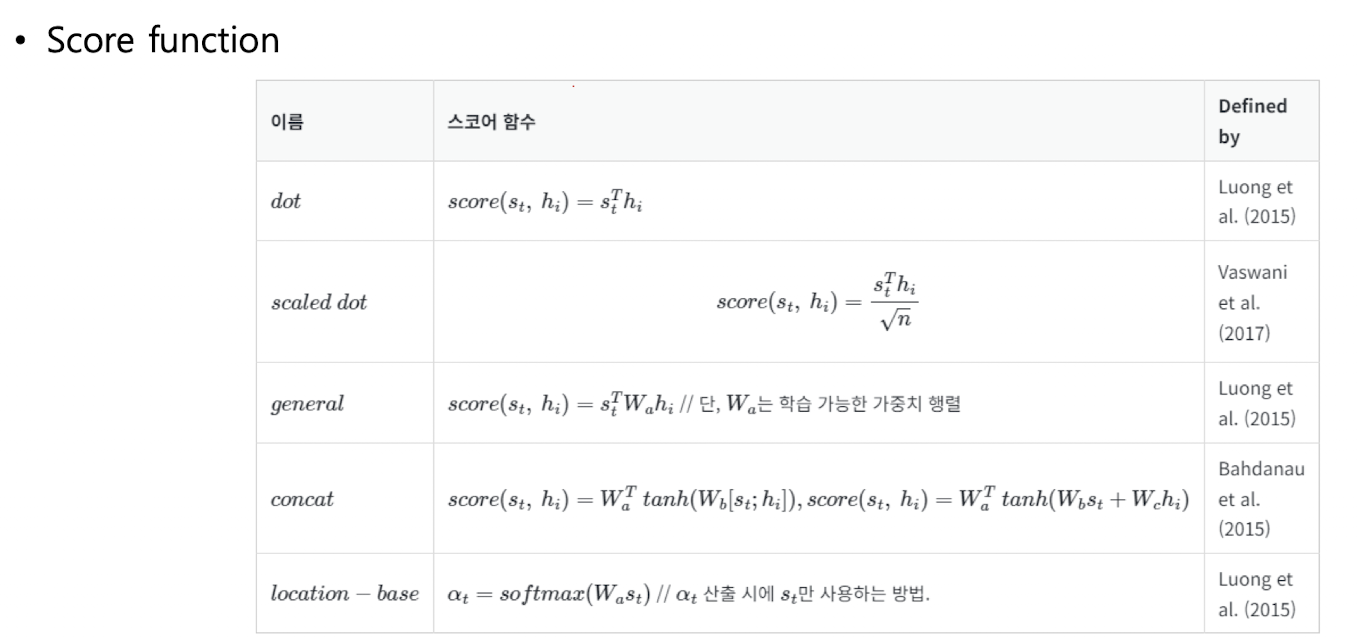
바꿀 수 있다.

---

Generalized form of attention

• $Q$: Query (질의) — 디코더의 타깃 은닉 상태
• $K$: Key (키) — 이 부분이 어떤 정보인지, 인코더의 모든 은닉 상태. 쿼리와 얼마나 비슷한지 비교하는 기준
• $V$: Value (값) — 이 부분의 정보를 얼마나 반영할지, 일반적으로 Key와 동일 (인코더의 은닉 상태)
• $d_k$: Key 벡터의 차원 수 (정규화를 위해 사용)

1. 유사도 계산

   • $Q K^T$: Query와 각 Key 사이의 내적(dot product)으로, Query(디코더 은닉 상태)가 Key(인코더 은닉 상태) 각각과 얼마나 비슷한지(관련 있는지) 계산한다.

2. 정규화(Scaling)

   • $\frac{Q K^T}{\sqrt{d_k}}$: 내적값을 $\sqrt{d_k}$로 나누어, 차원이 커질수록 값이 커지는 현상을 방지한다.

3. 소프트맥스(Softmax) 적용

   • $\text{softmax}\left(\frac{Q K^T}{\sqrt{d_k}}\right)$:
     각 Key에 대한 유사도 점수를 0~1 사이의 확률 분포로 변환한다(모든 값의 합이 1이 되도록).

4. Value와 곱하기(가중합)

   • 위에서 구한 소프트맥스 값(=attention weight, 각 Key의 중요도)을 Value에 곱해 가중합을 구한다.
   • 이 결과가 최종 attention output(context vector)로, 디코더가 다음 예측에 사용할 정보를 담는다.

Transformer

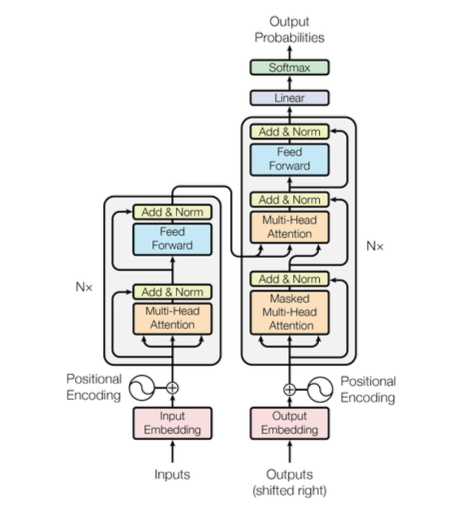
Multi-head attention : 입력 시퀸스에 대하여 어느 부분에 attention 해야 하는지 여러 개의 서로 다른 방식 (head)로 동시에 계산함

Feed_forward Network : 어텐션 블록 뒤에 위치하는 fc 신경망, 위치별로 독립적인 동일 FFN 적용

layer Normalization : 출력 정규화

Residual connection : 서브레이어에 앞뒤로 입력을 더해주는 구조

Positional Encoding : Transformer는 입력 시퀸스의 순서를 인식하지 못함. 즉 위치정보 더해준다.

Self-attention

입력 시퀸스 내의 각 요소가 다른 모든 요소와의 관게를 동적으로 계산

문장 내에서 세가지 역할로 변환된다.
HOW ? 입력값에 Wq Wk Wv 곱해서

Wo는 여러 헤드의 어텐션 결과를 다시 원래 차원으로 돌려주는 변환 행렬에 사용하는 가중치
Query : 유튜브 검색창에 입력하는 텍스트 프롬포트
Key : DB에 저장된 동영상 이름
Value : 실제 동영상

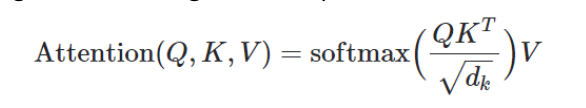
1. 입력 시퀸스의 각 요소에서 Q K V 벡터 생성
2. Q K 내적하여 쿼리와 키 간 유사도 검사. -> 차원수 d로 나누어 정규화
3. softmax 함수 적용 -> 얼마나 집중해야 할지 ?
4. 어텐션 가중치를 V와 곱하여 최종 출력을 얻을 수 있다.

Multi-head attention

입력을 여러개의 독립적인 어텐션 head로 나누고, 각 헤드는 서로 다른 Q K V를 가짐, 다양한 attention map 이 나온다. -> 각 헤드마다 관계 포착

해당 헤드들은 병렬적으로 작동. 즉 서로 다른 관점에서 정보 추출
각 헤드의 출력을 이어붙인 후 선형변환하여 하나의 특징벡터로 만듦.

예시

입력 단어 벡터의 차원 : 512
attention head : 8개

그렇다면 각 헤드 입력 벡터의 차원은 64개씩이다. 512/8

따라서 가중치 Wq Wk Wv 는 512개의 차원을 64개로 변환해야하므로 512 *64 필요

Wo는 다시 변환해야하므로 512*512

Masked Multi-Head attention

트랜스포머의 디코더가 미래 토큰을 보지 못하게 막는 역할
언어 생성에서는 현재까지의 단어만 보고 다음 단어를 예측해야하므로

이렇게 해야 디코더 훈련이 병렬로 가능해진다.

FFN

트랜스포머 블록 내에서 어텐션 계층 다음에 위치
각 토큰의 표현을 독립적으로 변환하는 역할

어텐션 : 문맥 정보를 섞어줌
FFN : 복잡한 특징 추가

Layer Normalization

트랜스포머에서 각 토큰의 특징 벡터를 독립적으로 정규화

Residual Connection

한 레이어의 입ㄹ겨을 출력에 더해 다음레이어로

Pre-norm design

정규화를 서브레이서 앞에
널리쓰임

위치 인코딩

문장 내에서 단어 순서 정보 모르니까 직접 넣어주기

Vision Transformer

2차원 이미지를 일정 크기의 패치로 잘라내어 1차원 벡터로 임베딩
각 패치를 토큰처럼 처리하고 위치 인코딩을 더해 트랜스포머에 입력