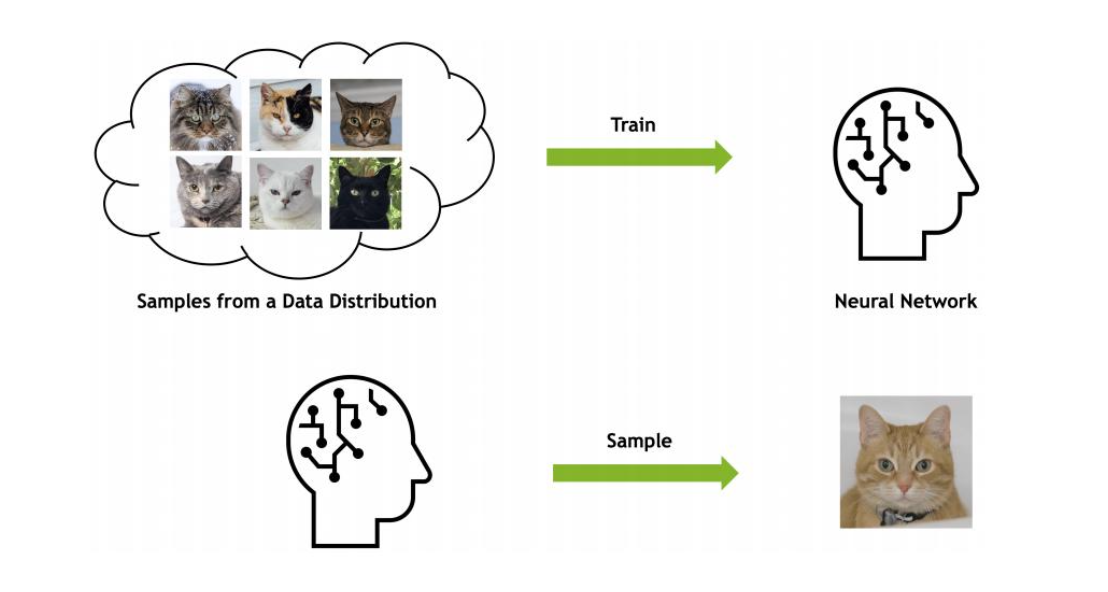
Generative Models : 여러 변수에 대한 확률 분포를 출력. 실제 데이터를 생성하는 분포를 학습한다. 이를 통하여 약간의 변형이 있는 새로운 데이터 생성 가능

---

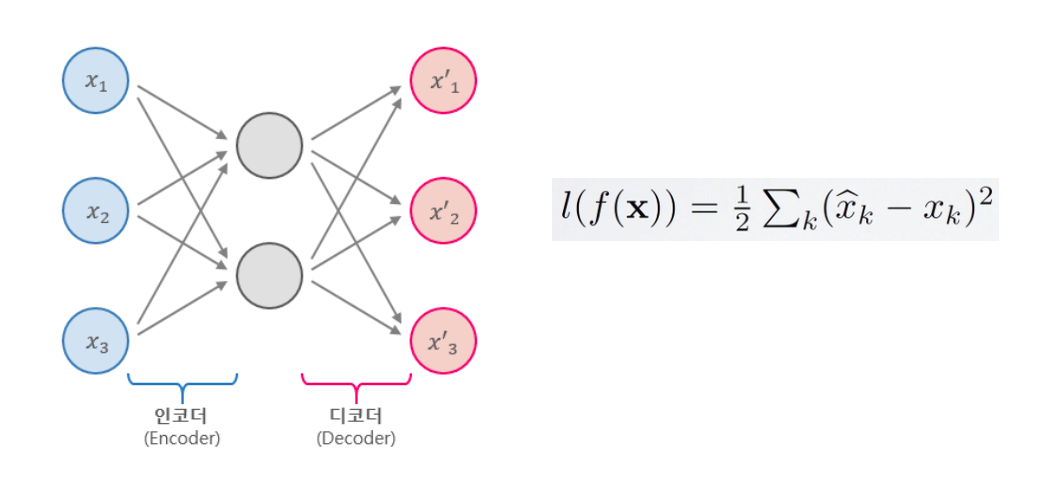
Autoencoder

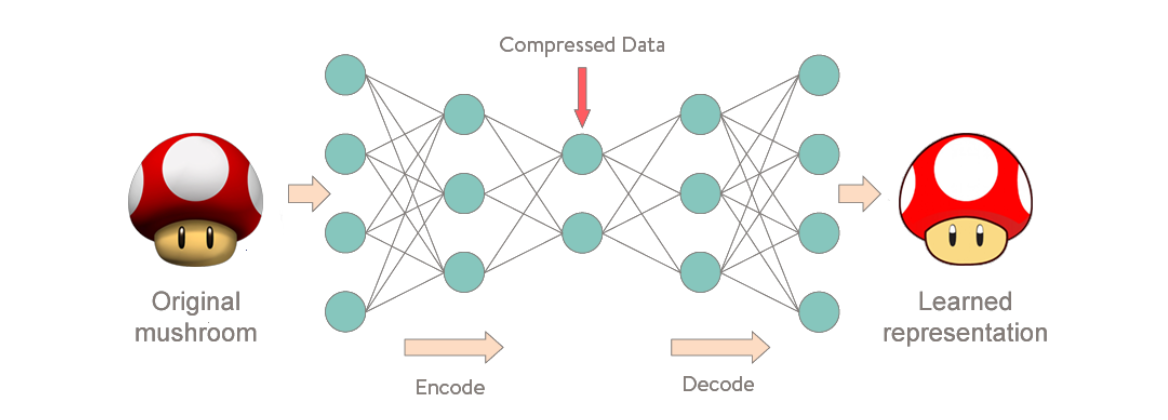
입력 데이터를 인코딩하여 압축하고, 다시 디코딩하여 원본 데이터를 복원하는 비지도 학습 모델

Undercomplete Autoencoder

입력 데이터의 차원보다 더 작은 차원의 hidden layer를 갖는 오토인코더. 입력을 그대로 복사하여 출력으로 만들 수 없기 때문에, 모델은 입력 데이터에서 가장 중요한 특성을 압축하여 히든 레이어에 담는다.

• 우리의 관심 대상은 h (히든 레이어의 표현)
  - 재구성된 출력이 아니라 h에 집중. 입력 데이터의 본질적인 특징(가장 중요한 정보)를 담고 있음.
• 입력 차원을 강제로 줄임
• 일종의 차원 축소 기법, 선형 오토인코더의 경우 PCA(주성분 분석)과 유사하게 동작. 하지만 오토인코더는 비선형 변환도 가능하다는 점에서 더 복잡하다.

• 오토인코더의 손실 함수(재구성 오차)를 나타내는 수식
• $l(f(\mathbf{x}))$는 입력 $\mathbf{x}$를 인코더와 디코더를 거쳐 복원한 뒤, 원본과 복원본의 차이를 계산한 값
• $\hat{x}_k$는 복원된 데이터의 k번째 값, $x_k$는 입력 데이터의 k번째 값
• 각 특성별로 $(\hat{x}_k - x_k)^2$의 제곱 오차를 모두 더하고, $\frac{1}{2}$를 곱해 평균 오차를 구함
• 값이 작을수록 오토인코더가 입력을 더 정확하게 복원했다는 의미

---

Usage of autoencoders

오토인코더의 사용법

Feature extraction 특징 추출

특징 추출 : 입력 데이터에서 의미 있는 특징을 자동으로 추출하는 과정
-> 코드 벡터(feature map.. 등)는 입력 데이터를 잘 대표할 수 있는 좋은 표현. 원본 데이터의 중요한 정보를 압축하여 담고 있음

Novelty detection 이상 탐지

이상 탐지 : 훈련 데이터에서 보지 못한 새로운 패턴(훈련에 사용되지 않은 샘플)을 테스트 데이터에서 식별하는 작업

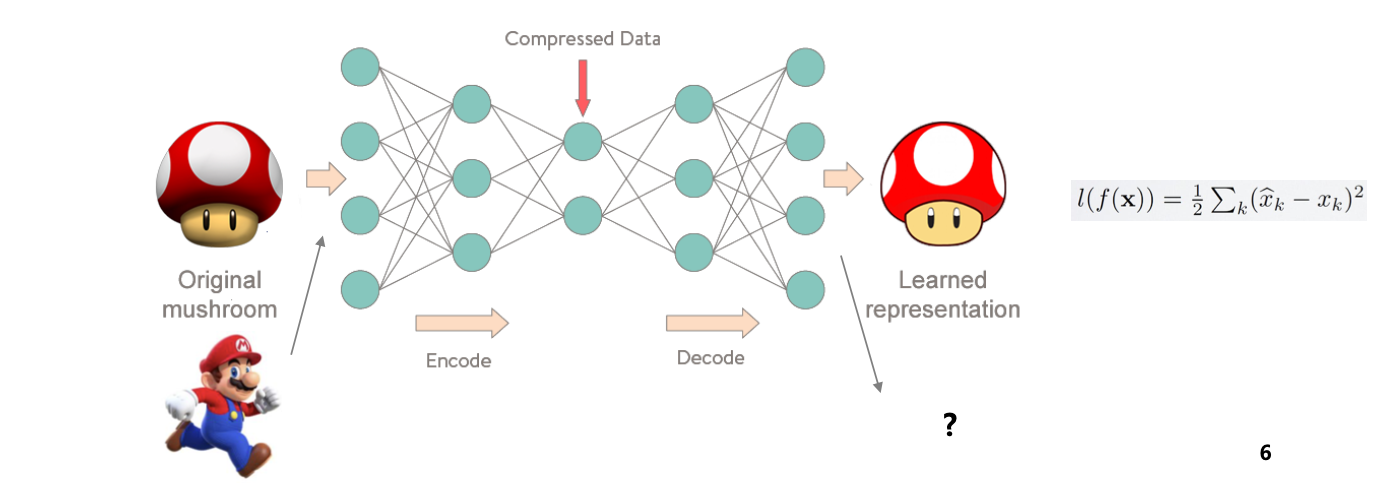
수집한 입력 데이터(원본 버섯)을 복원한 출력 데이터(복원 버섯) 사이의 오차를 의미. 해당 로스를 최소화하는 방향으로 네트워크가 학습된다.

---

Stacked (deep) autoencoder

여러개의 오토인코더를 층층이 쌓아 올린 구조. 오토인코더를 여러 계층으로 구성하여 더 복잡하고 추상적인 특징을 추출할 수 있게 만든다.

일반적인 deep feedforward nerual networks와 같은 장점

복잡한 비선형 구조를 더 잘 학습할 수 있고, 더 강력한 표현력을 가진다.

파라미터 공유

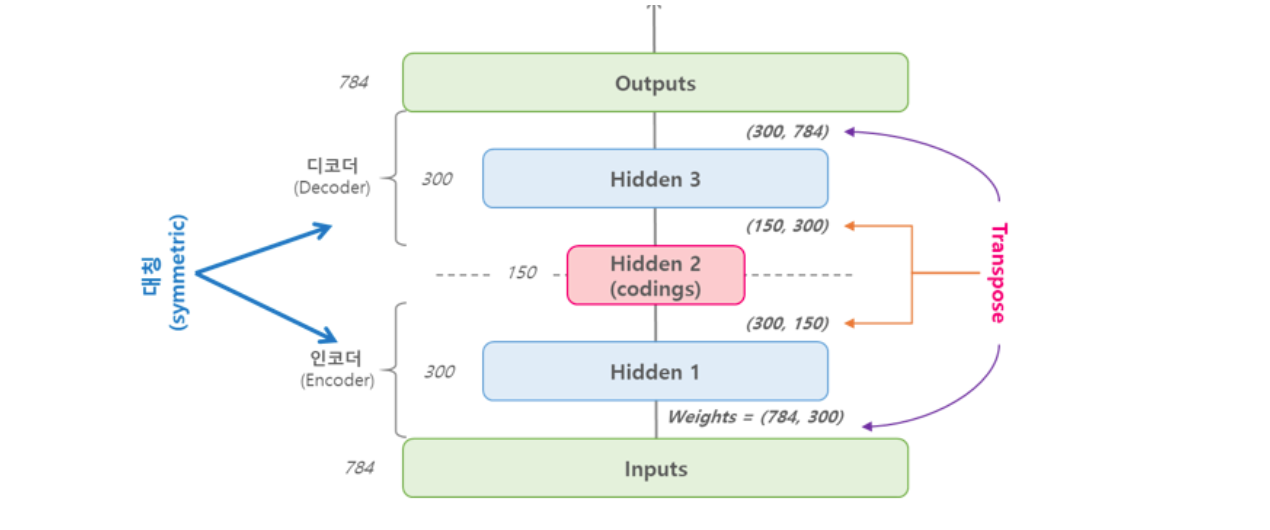
인코더와 디코더 부분에서 weight를 공유하거나 묶음. 디코더의 가중치를 인코더 가중치의 transpose로 한다.
파라미터 수를 줄여 시간과 리소스를 줄이고, 과적합 위험을 낮추며 학습을 더 안정적으로 가져감.

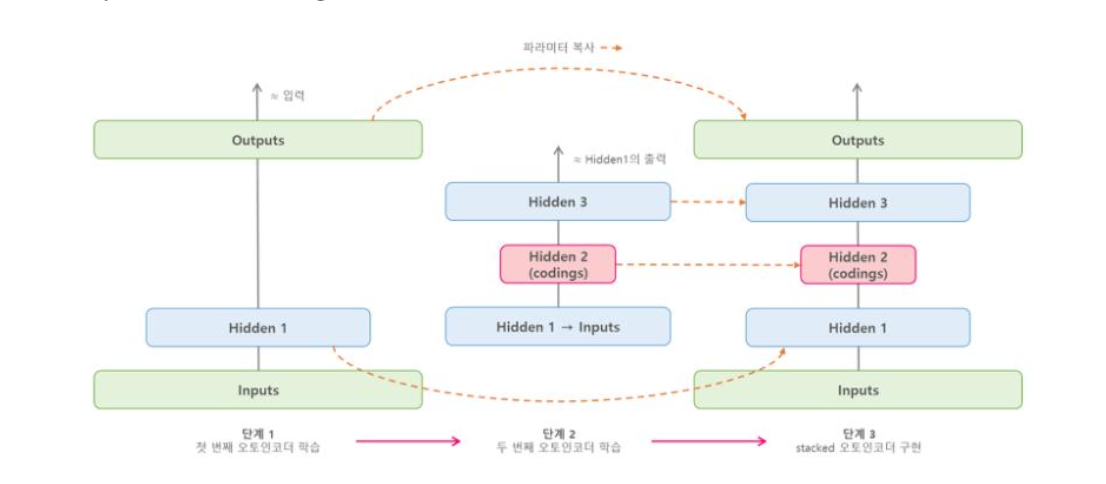
순차적 학습 방식

오토인코더는 각 층을 한번에 모두 학습하는 것이 아니라, 한 층씩 차례로 학습시켜 쌓아가는 방법

1. 첫 번째 오토인코더를 사용하여 입력 데이터 재구성 ( 오토인코더는 입력 데이터를 압축(은닉층)했다가 다시 복원하여 출력). 최대한 복원된 출력이 입력과 비슷해지게 학습. --> 입력 데이터의 중요한 특징을 뽑아내는 법을 학습

2. 두 번째 오토인코더는 첫 번째 오토인코더의 은닉층에서 나온 결과, 즉 특징 벡터를 새로운 입력 데이터로 사용. 해당 특징벡터를 또 압축했다가 복원 -> 더 추상적인 특징을 뽑아낼 수 있음

3. 앞서 학습한 각 오토인코더의 weight를 복사하여 연결, 미세조정하여 더 강력한 신경망 만들 수 있음
   

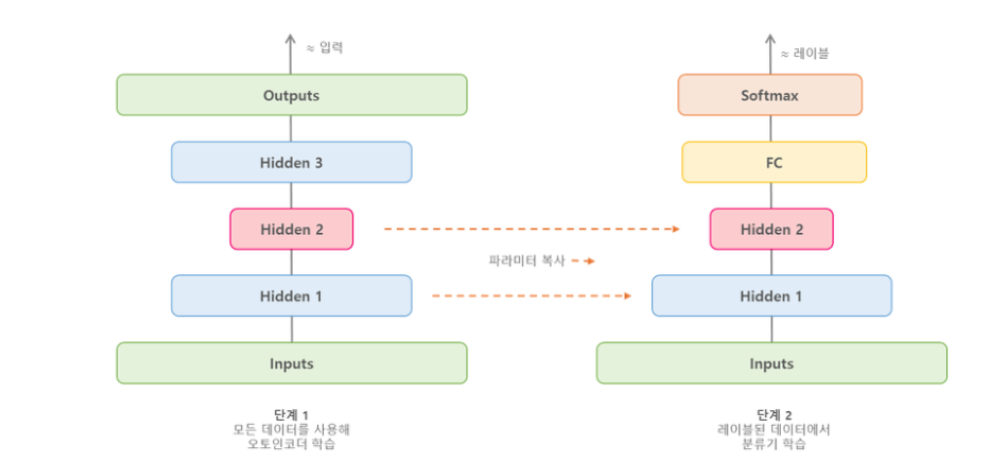
사전학습 도구로서 stacked autoencoder

1단계 : 오토인코더로 비지도 사전학습
- 모든 데이터 사용

2단계 : 분류기 학습
- 레이블이 있는 데이터만 사용
- 왼쪽에서 학습한 오토인코더의 가중치를 복사하여 초기값으로 사용
- FC와 Softmax function으로 실제 분류 작업을 위한 학습 진행

---

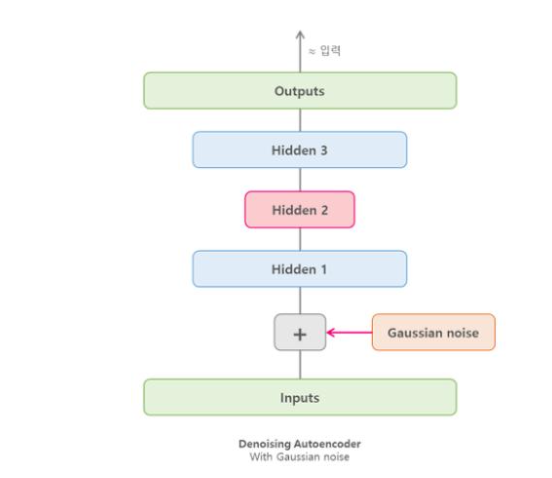
Denoising autoencoder DAE

입력 데이터에 인위적으로 노이즈를 추가 한 뒤, 노이즈가 섞인 데이터를 원래의 깨끗한 데이터로 복원하도록 학습

Robust model with added noise : Loss function

robust : 과적합에 덜 민감하고, 새로운 데이터에도 잘 작동

1. 노이즈 추가

   • 원본 입력 $\mathbf{x}$에 노이즈를 더해 $\tilde{\mathbf{x}} = \mathbf{x} + \text{noise}$ 형태의 데이터를 만듦
   • 예시: 이미지에 랜덤 픽셀 노이즈, 오디오에 잡음 추가 등

2. 입력과 출력

   • 입력: 노이즈가 추가된 데이터 $\tilde{\mathbf{x}}$
   • 출력: 네트워크가 복원한 데이터 $\hat{\mathbf{x}}$
   • 정답(타깃): 원본 데이터 $\mathbf{x}$

3. 손실 함수 (Loss Function)

   • 네트워크는 $\tilde{\mathbf{x}}$를 입력받아 $\hat{\mathbf{x}}$를 출력
   • 손실 함수는 원본 데이터와 복원된 데이터의 차이(예: 평균 제곱 오차)를 계산
   • 수식 예시:
     $L(\mathbf{x}, g(f(\tilde{\mathbf{x}})))$
     여기서 $f$는 인코더, $g$는 디코더, $\tilde{\mathbf{x}}$는 노이즈가 추가된 입력

Robust model with dropout

학습할 때 신경망의 일부 뉴런을 무작위로 drop out 즉, 죽이는(끄는) 방식

overfitting 방지, 일반화 성능 향상, 특정 뉴런의 의존성 감소 ... 등

---

Convolution autoencoder CAE

공간적 구조가 있는 데이터를 효과적으로 처리하기 위해 고안된 오토인코더의 한 종류. 일반 오토인코더와 달리 합성곱 사용!

입력 이미지를 여러 합성곱 + 풀링 계층을 거치며 10차원의 feature map 으로 압축

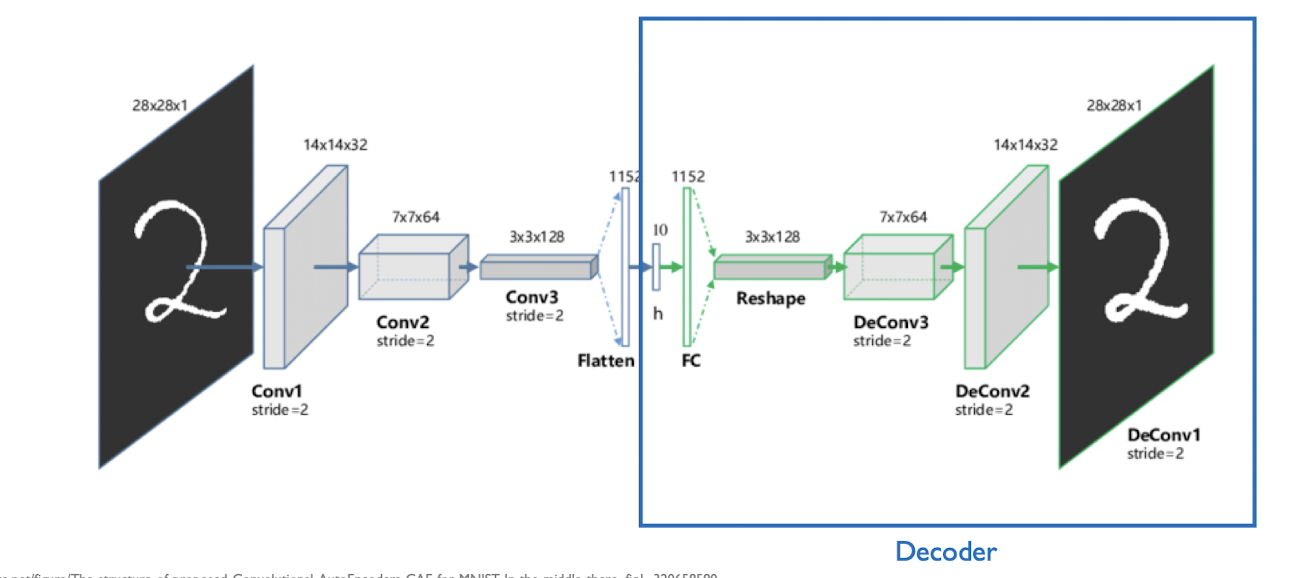
latent space를 다시 3*3*128 텐서로 변환한다.

Unpooling

디코더의 복원 과정에서, pooling으로 줄어든 feature map을 다시 원래 크기로 재구성
-> 최대값이 어디서 나왔는지를 기록하고, 나머지 위치는 0으로 기록한다.

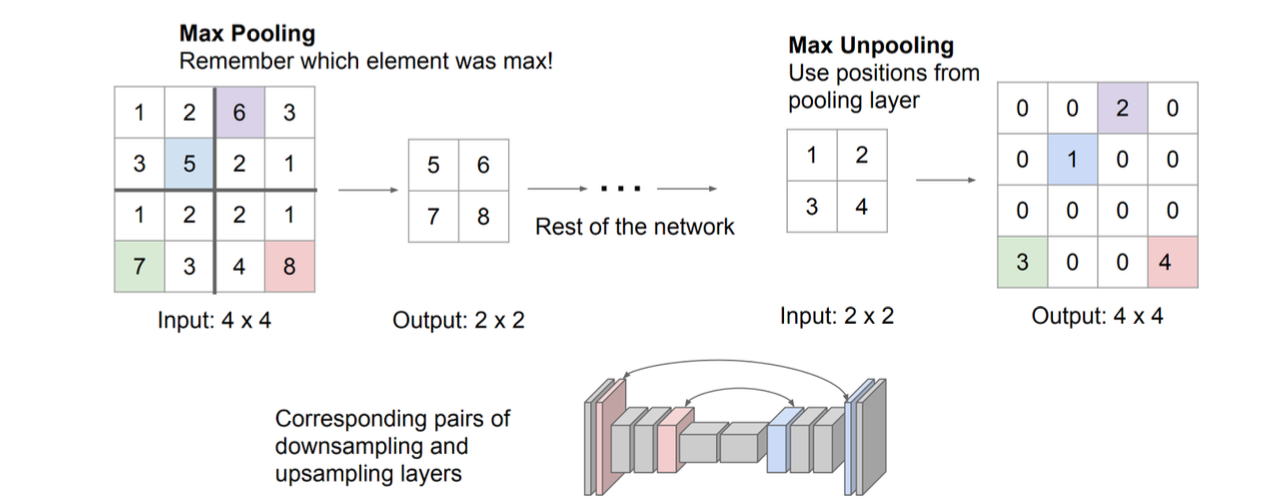
맥스 풀링 할 때 위치정보만 남겨두기. 완전한 역연산이 아니기 때문에 숫자는 달라질 수 있지만, 해당 위치에 Max 값이 있었다. 는 동일

Transpose Convolution

역합성곱. 복원할 때 사용. 마찬가지로 신호처리에서의 Deconvolution과는 조금 다른 개념이지만 그냥 Deconvolutional Layer라고 부르기도 한다.

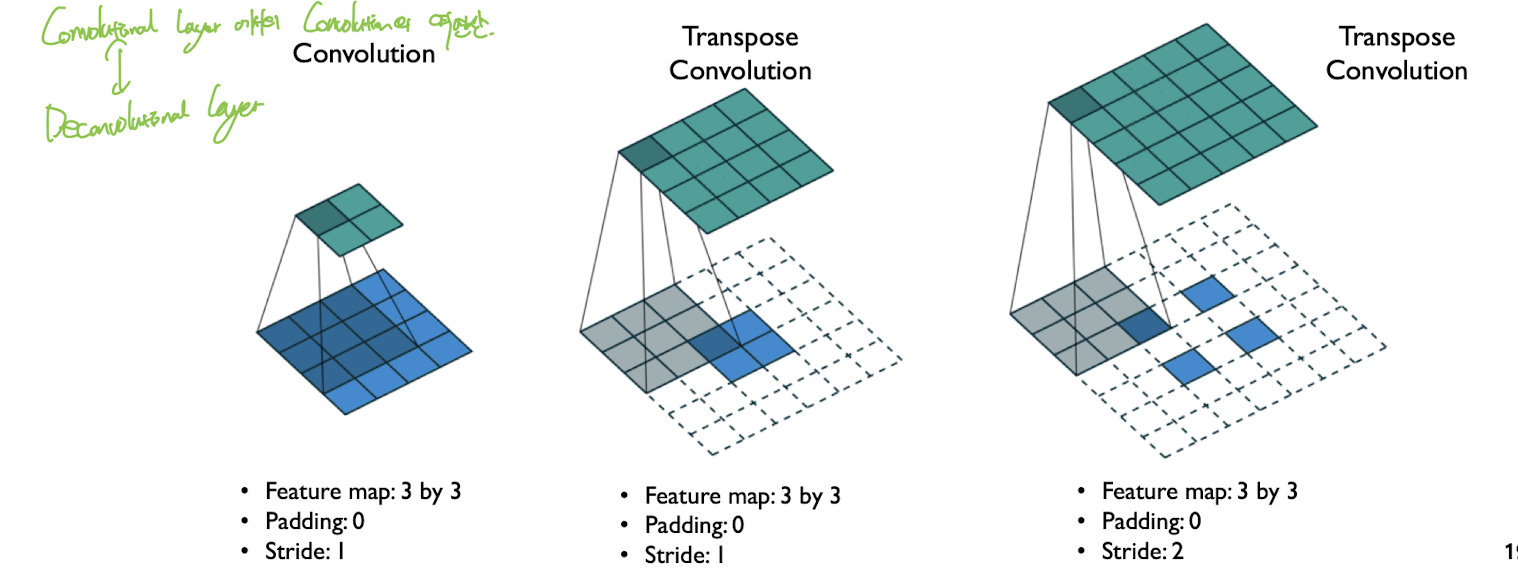
작은 feature map을 받아, 더 큰 feature map 으로 upsampling

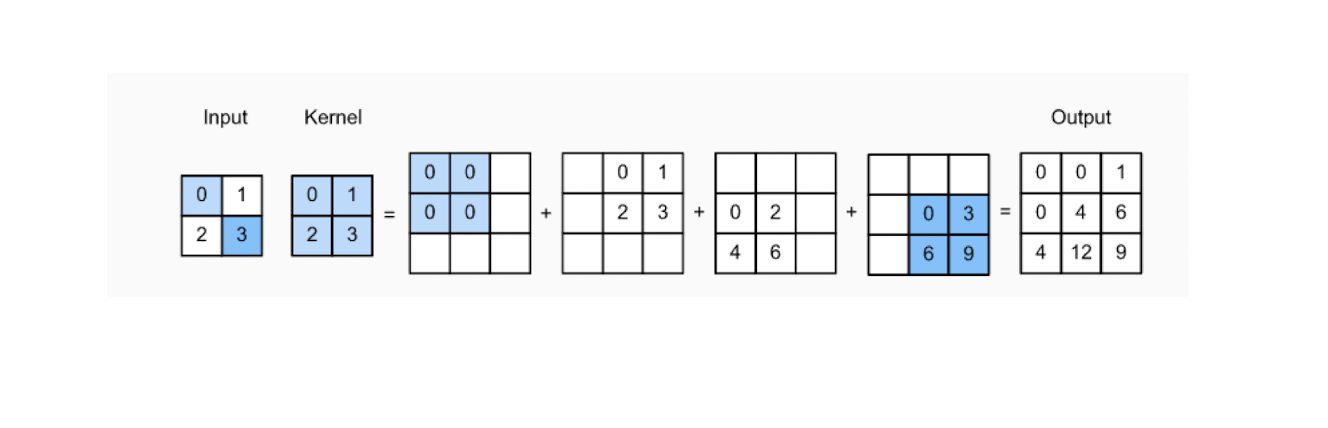
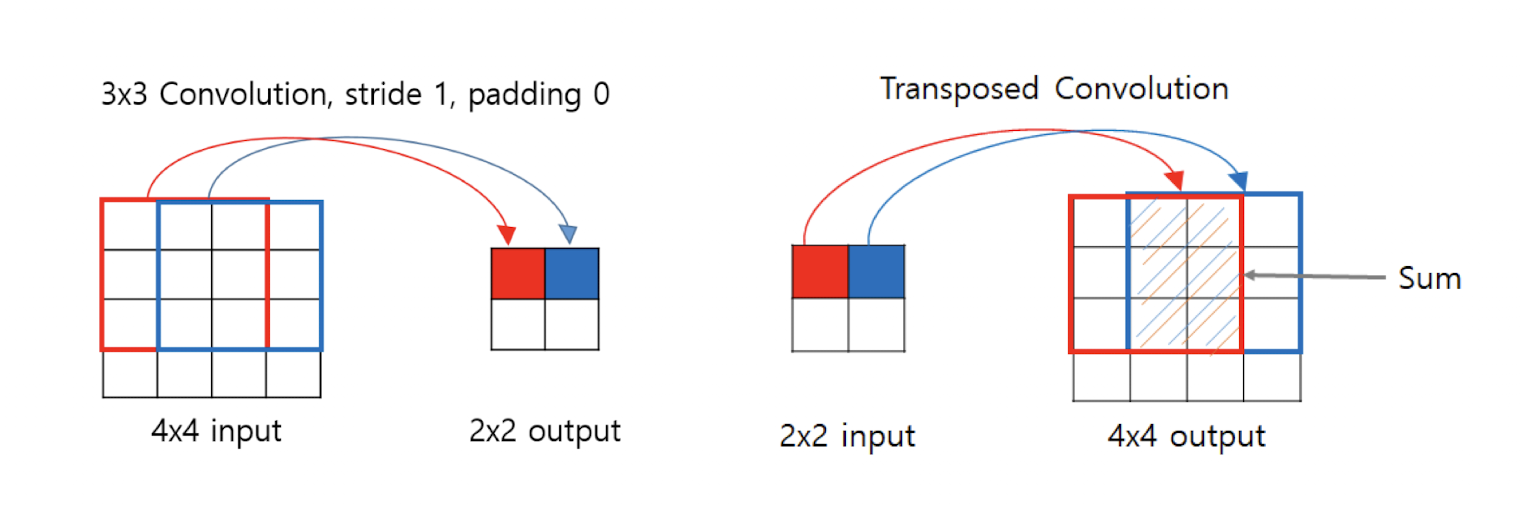
그림 보면 이해가 잘 됨, 그냥 Convolution 연산의 역연산이라고 생각하자. 겹치는 부분은 단순 sum

---

Deep Generative Models

Discriminative model과 같은 분류 문제를 풀 수 있다.

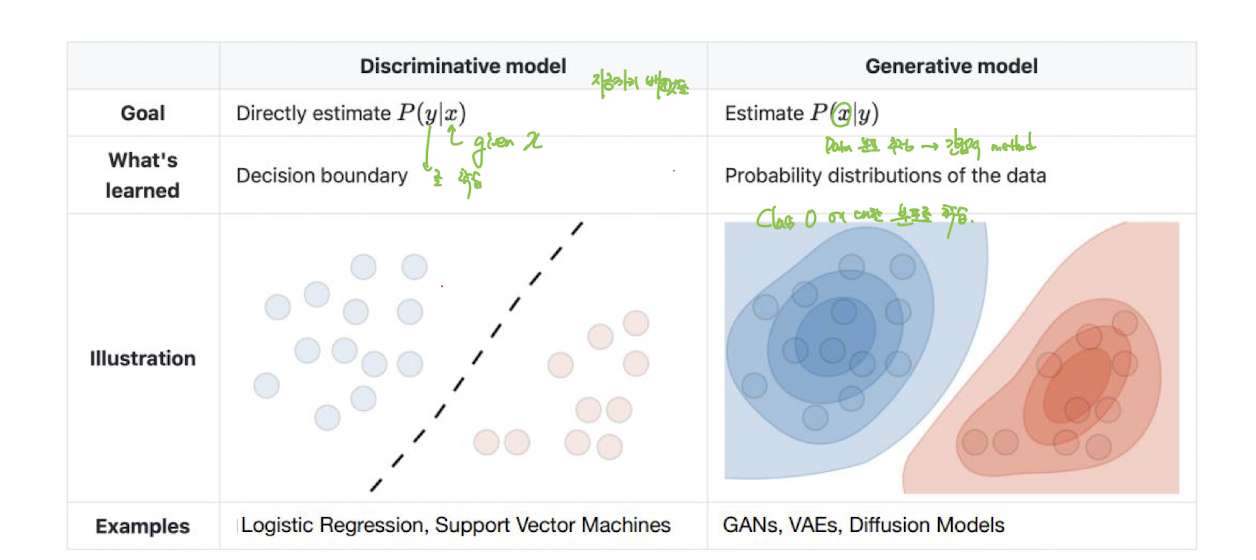
Discrimination 모델 : 결정 경계를 학습한다.
Generative 모델 : 데이터의 확률 분포를 학습

Variational autoencoder VAE

입력 데이터에서 연속적인 latent variable (잠재 변수)를 갖는 확률적 생성 모델을 효율적으로 학습시키기 위한 방법
입력의 분포를 추정(가우시안 분포의 평균과 표준편차)

• VAE는 입력 데이터에서 latent space z로 mapping, z로부터 다시 데이터를 생성(복원)하는 구조
• posterior은 계산이 복잡함. 실제로 더 단순한 분포로 근사해야 하는데, 이때 효율적인 근사를 추론하기 위하여 VAE 구조를 사용한다.

---

이미지 데이터셋이 주어졌을 때, 데이터의 분포 P(X) 자체를 모델링하려고 한다. P(X)를 직접 학습하는건 정말 어렵고, P(X)의 분포를 근사하는 다른 분포 Q(X)를 찾아주는것

• $X$ is connected to a latent space $z$, $P(z|X)$
  → 여기서 $X$는 실제 데이터(예: 이미지, 텍스트 등)를 말하고, $z$는 그 데이터가 가진 '숨겨진 특징'이나 '요약 정보'를 담는 잠재 변수(latent variable)를 의미함.
  → "확률적으로 연결되어 있다"는 건, 어떤 $X$가 주어졌을 때 $z$가 어떤 값을 가질 확률 $P(z|X)$로 표현할 수 있다는 뜻임. 즉, 데이터 $X$와 그로부터 추출할 수 있는 잠재 변수 $z$ 사이에 확률적(불확실성, 다양성 포함) 관계가 있다는 의미임.
  → 예를 들어, 고양이 사진 $X$가 주어지면, 그 사진을 요약하는 여러 가지 $z$ (털 색, 귀 모양 등)가 있을 수 있고, 이 $z$는 확률적으로 결정됨.

• Instead of calculating $P(z|X)$ (difficult), we will find a simpler distribution $Q(z|X)$
  → $P(z|X)$는 복잡해서 직접 계산하기 어렵기 때문에, 실제로는 더 단순한 분포 $Q(z|X)$로 근사해서 사용함.
  → 이 $Q(z|X)$는 보통 정규분포처럼 다루기 쉬운 분포로 가정하고, 인코더가 $X$를 입력받아 $z$의 평균과 분산을 출력하게 만듦.

• For example, $Q \sim N(\mu, \sigma^2)$
  → 예를 들어, $Q$는 평균 $\mu$, 분산 $\sigma^2$를 갖는 정규분포로 가정할 수 있음. 즉, 인코더가 $X$에서 $z$의 평균과 분산을 구하고, 그걸로부터 $z$를 샘플링함.

---

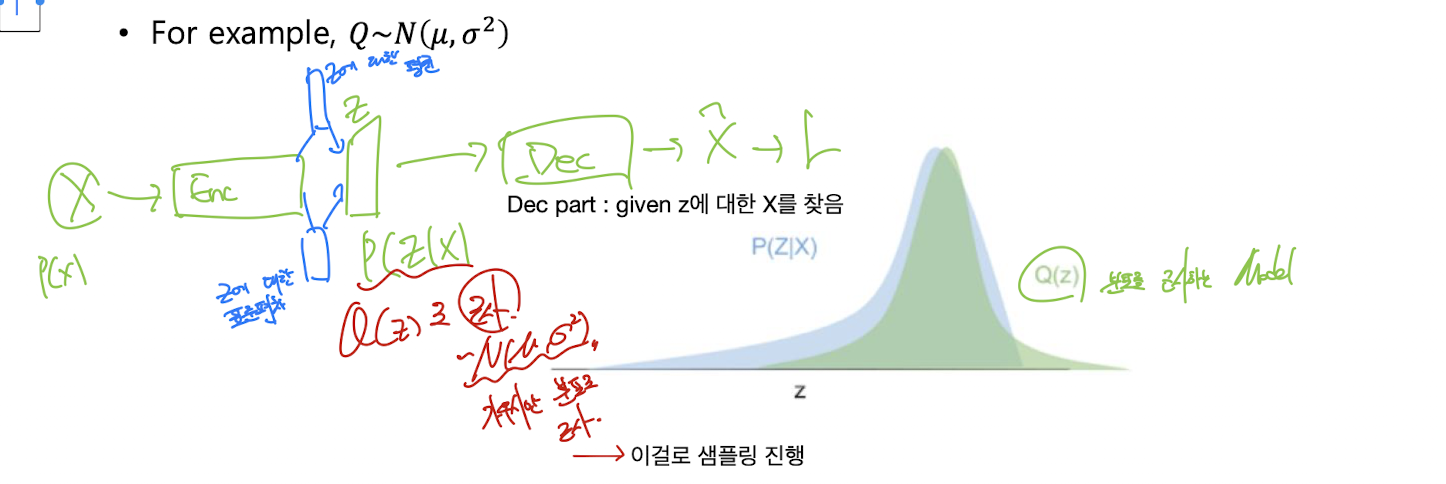
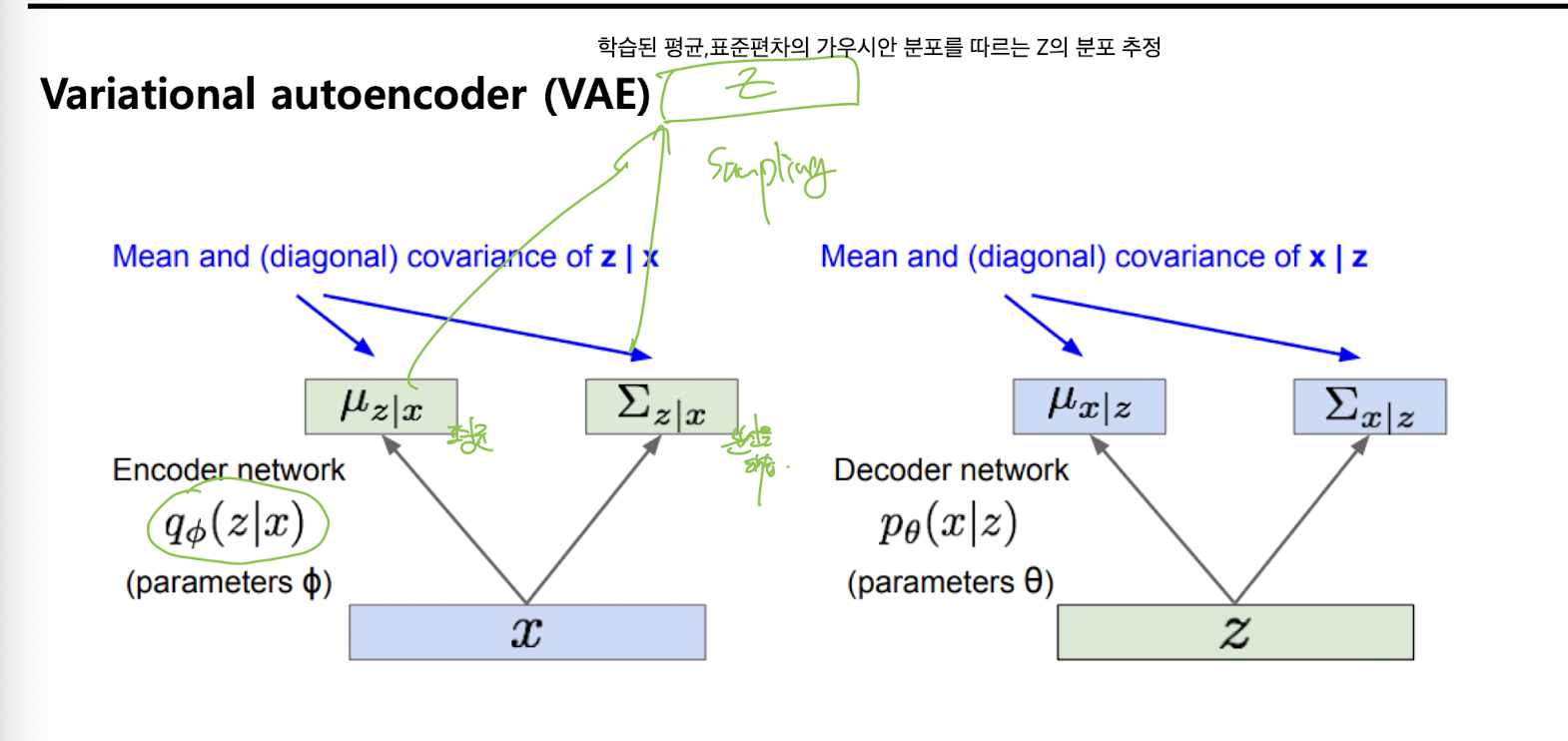
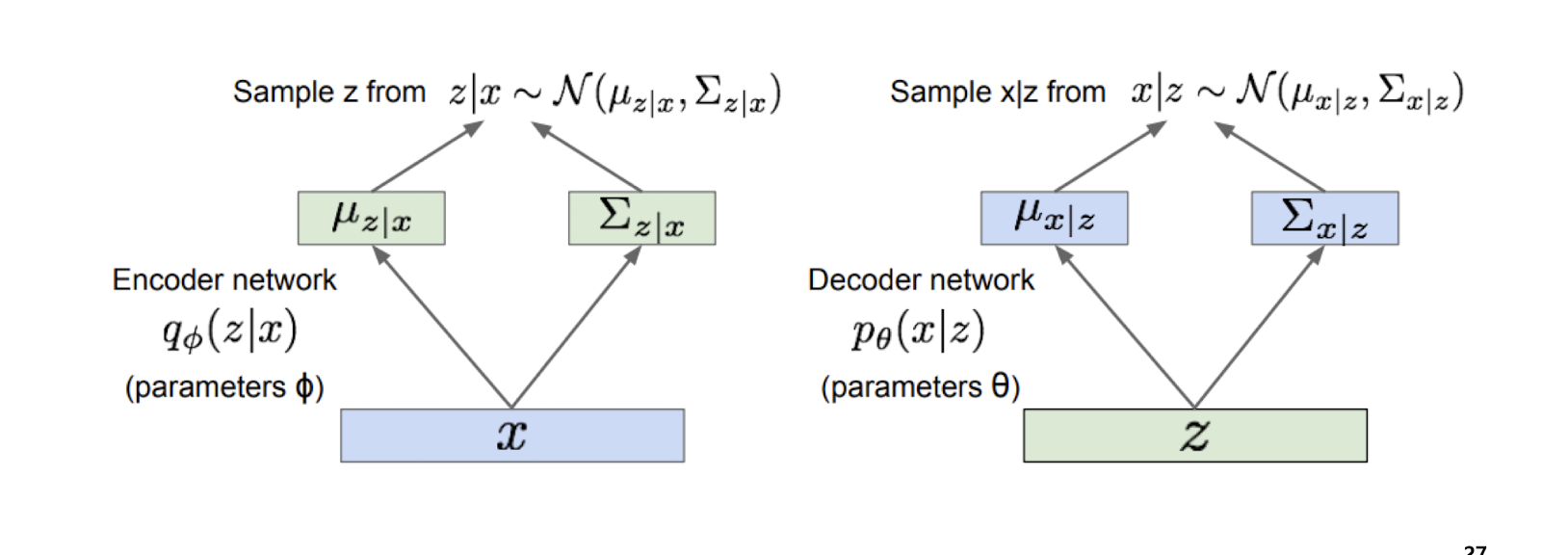
1. 인코더 네트워크 $q_\phi(z|x)$

• $x$: 입력 데이터 (예: 이미지, 텍스트 등)
• 인코더(Encoder): $q_\phi(z|x)$
  • $x$를 입력받아, 잠재 변수 $z$의 분포(평균 $\mu_{z|x}$, 분산 $\Sigma_{z|x}$)를 출력
  • 즉, $x$를 보고 "이 데이터의 잠재 벡터 $z$는 어떤 값일까?"를 확률적으로 예측
  • $\mu_{z|x}$, $\Sigma_{z|x}$: $z$의 평균과 분산(공분산행렬), 각각 인코더 신경망의 출력값
• 샘플링(Sampling)
  • $z$는 $z|x \sim \mathcal{N}(\mu_{z|x}, \Sigma_{z|x})$에서 무작위로 뽑음
  • 이 과정에서 reparameterization trick을 써서 미분 가능하게 만듦

---

2. 디코더 네트워크 $p_\theta(x|z)$

• $z$: 인코더에서 샘플링된 잠재 변수
• 디코더(Decoder): $p_\theta(x|z)$
  • $z$를 입력받아, 원래 데이터 $x$의 분포(평균 $\mu_{x|z}$, 분산 $\Sigma_{x|z}$)를 출력
  • "이 $z$가 주어졌을 때, 어떤 $x$가 나올 확률이 높을까?"를 예측
  • $\mu_{x|z}$, $\Sigma_{x|z}$: $x$의 평균과 분산(공분산행렬), 각각 디코더 신경망의 출력값
• 샘플링(Sampling)
  • $x$는 $x|z \sim \mathcal{N}(\mu_{x|z}, \Sigma_{x|z})$에서 샘플링 가능
  • 실제 학습에서는 $\mu_{x|z}$만 사용해서 복원 이미지를 만듦

---

3. 전체 흐름

4. 입력 $x$ → 인코더 → 잠재 분포 파라미터($\mu_{z|x}$, $\Sigma_{z|x}$) 산출

5. $z$를 정규분포 $\mathcal{N}(\mu_{z|x}, \Sigma_{z|x})$에서 샘플링

6. $z$ → 디코더 → 복원 분포 파라미터($\mu_{x|z}$, $\Sigma_{x|z}$) 산출

7. $\mu_{x|z}$를 복원 데이터로 사용하거나, $\mathcal{N}(\mu_{x|z}, \Sigma_{x|z})$에서 $x$ 샘플링

---

4. 왜 확률 분포로 표현하는가?

• 일반 오토인코더는 $x \to z \to x'$로 '고정된 벡터'만 다룸
• VAE는 $x$를 '분포'로 바꿔서, $z$를 다양하게 샘플링할 수 있게 함
• 이 구조 덕분에 새로운 $z$를 뽑아도 그럴듯한 $x$를 만들 수 있고, 생성 모델로 활용 가능

---

5. 수식 요약

• 인코더: $q_\phi(z|x) = \mathcal{N}(\mu_{z|x}, \Sigma_{z|x})$
  - x를 받아서 z라는 잠재 변수가 어떤 분포를 가질지 예측한다. phi는 파라미터. q는 분포를 의미
• 디코더: $p_\theta(x|z) = \mathcal{N}(\mu_{x|z}, \Sigma_{x|z})$

---

6. 직관적 예시

• $x$: 고양이 사진 한 장
• 인코더: "이 사진의 특징(귀, 눈, 털 등)을 요약하면 평균 $\mu_{z|x}$, 분산 $\Sigma_{z|x}$로 표현할 수 있다"
• $z$ 샘플링: "고양이 사진의 다양한 변형(귀 크기, 털색 등)이 $z$에서 무작위로 뽑힘"
• 디코더: "이 $z$를 바탕으로 다시 고양이 사진을 복원"

---

7. 결론

• VAE는 입력 $x$를 잠재 공간 $z$의 확률분포로 변환(인코더), $z$에서 다시 $x$를 복원(디코더)하는 구조
• 각 단계에서 평균과 분산을 출력해, 다양한 $z$와 $x$를 샘플링할 수 있음
• 이 덕분에 새로운 데이터 생성, 데이터의 다양성 확보, 부드러운 잠재 공간 구조 등이 가능해짐

---

Log probability of the observation X

관측 데이터 x가 만든 모델에서 나올 확률이 얼마나 되는가를 계산해보자. 해당 함수를 손실 함수로 사용.

$x^{(i)}$: 실제로 관찰한 데이터 샘플
$p_\theta(x^{(i)})$: 모델이 학습한 확률분포에서 $x^{(i)}$가 나올 확률
$\log p_\theta(x^{(i)})$: 그 확률의 로그값 (값이 클수록 모델이 $x^{(i)}$를 잘 설명한다는 뜻)
VAE는 $\log p_\theta(x^{(i)})$의 값을 최대화(=loss를 최소화)하는 방향으로 학습함

---

관측값 $x^{(i)}$의 로그 확률을 근사 분포 $q_\phi(z|x^{(i)})$에 대해 기대값으로 표현

베이즈 정리로 전개

분자/분모에 $q_\phi(z|x^{(i)})$ 곱하고 나누기

로그 분리

KL Divergence(두 확률분포가 얼마나 다른지 측정하는 값)로 표현, 마지막 항은 항상 0 이상,
나머지 두 항이 Evidence Lower Bound (ELBO)가 됨. ELBO를 최대화하는 방향으로 학습

---

• $\mathcal{L}(x^{(i)}, \theta, \phi)$: 변분 하한(ELBO, Evidence Lower Bound)

  • 실제 로그 확률 $\log p_\theta(x^{(i)})$의 아래쪽 경계(최소값 역할)를 하는 값
  • 두 부분으로 구성됨

  1. 재구성 항

     $\mathbb{E}_{z \sim q_\phi(z|x^{(i)})} [ \log p_\theta(x^{(i)}|z) ]$
     • $z$를 샘플링해서 $x^{(i)}$를 얼마나 잘 복원하는지 평균(기댓값)
     • 인코더가 만든 $z$로 디코더가 $x^{(i)}$를 복원할 확률의 로그값의 평균
     • 값이 클수록 복원이 잘 된다는 뜻

  2. 정규화 항(KL Divergence)

     $- D_{KL}( q_\phi(z|x^{(i)}) \,\|\, p_\theta(z) )$
     • 인코더가 만든 $z$의 분포($q_\phi(z|x^{(i)})$)가 사전분포($p_\theta(z)$, 보통 표준 정규분포)와 얼마나 가까운지 측정
     • 값이 작을수록 두 분포가 비슷하다는 뜻 (즉, 잠재 공간이 잘 정규화됨)

• 실제 로그 확률은 ELBO보다 항상 크거나 같음(ELBO가 아래쪽 경계)
• ELBO를 최대화하면 실제 로그 확률도 같이 커짐

• 모든 데이터 샘플 $x^{(i)}$에 대해 ELBO의 합을 최대화하는 $\theta, \phi$를 찾음
• 즉, 모델 파라미터를 업데이트할 때 실제 로그 확률 대신 ELBO를 최대화하는 방향으로 학습함

---

VAE Encoder

입력 데이터 x를 잠재 표현 z로 변환하는 신경망이다. 파라미터는 $\psi$
given x, z의 근사분포 q를 추정 (정규분포로)

VAE Decoder

latent space z를 출력 x로 변환, 파라미터는 $\theta$
출력 확률 분포는 p

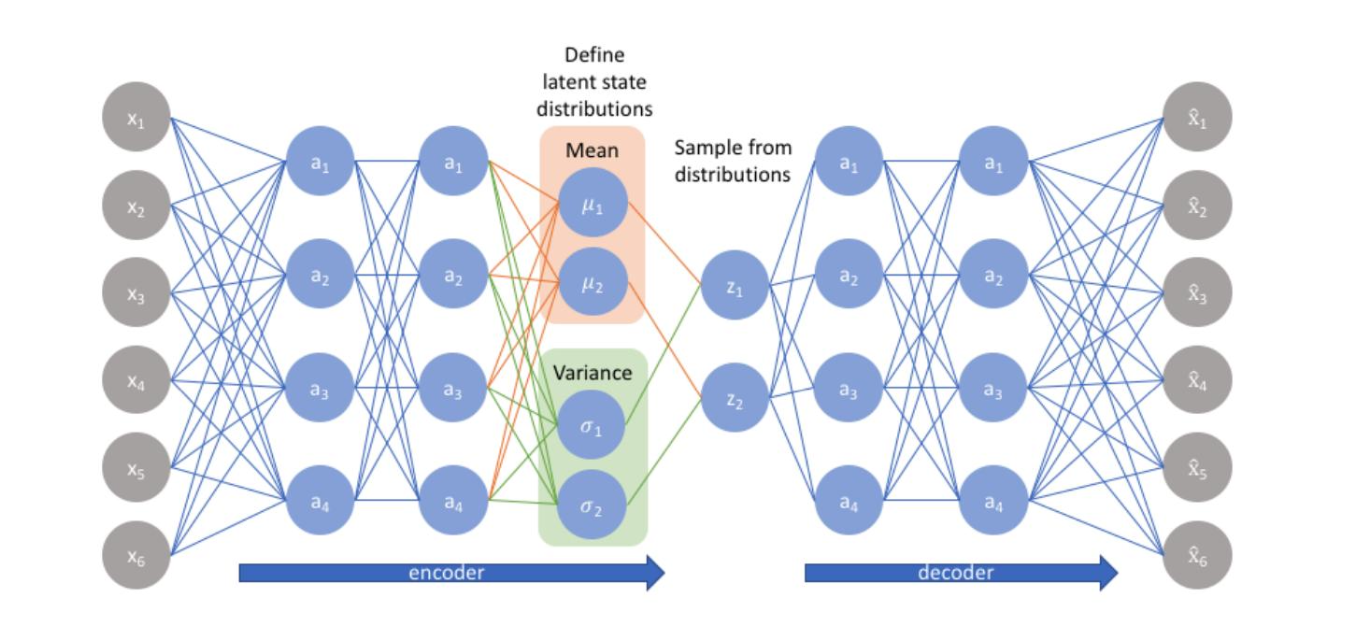
왼쪽 회색 노드는 입력
인코더 파트의 파란색 노드는 입력 데이터를 더 추상적으로 압축
그리고 인코더의 마지막 층에서 각 latent variable의 평균과 분산값을 출력한다.
그리고 해당 평균과 분산을 이용하여 sampling (reparameterization trick 이용) -> latent representation z

디코더는 샘플링된 z를 받아 출력을 복원한다.

---

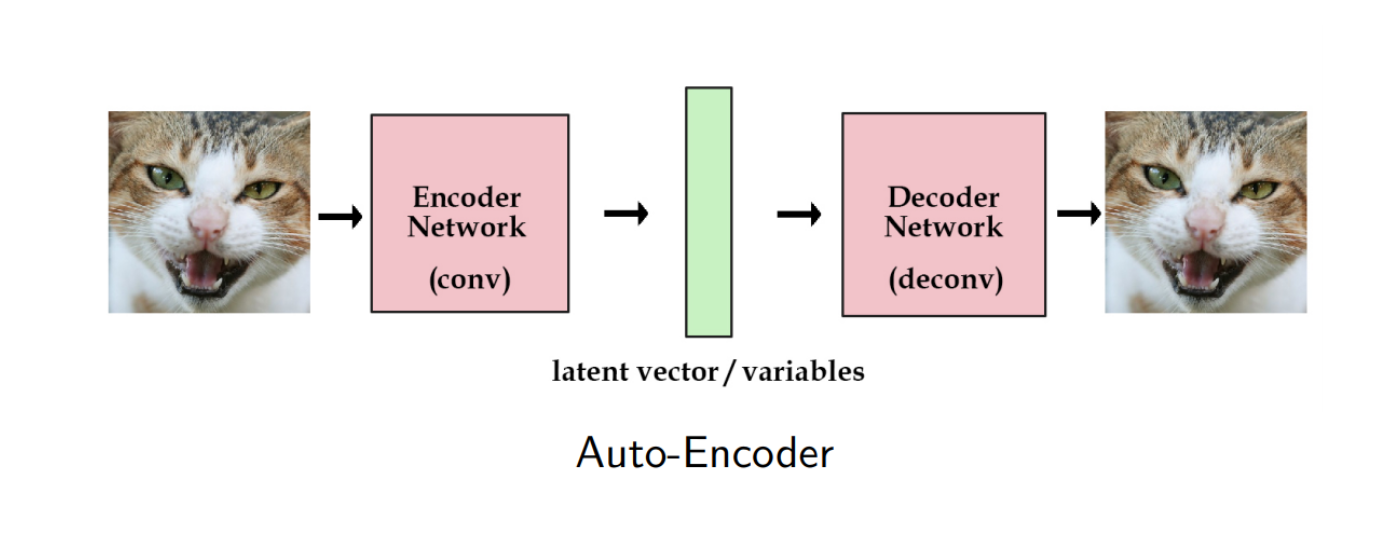
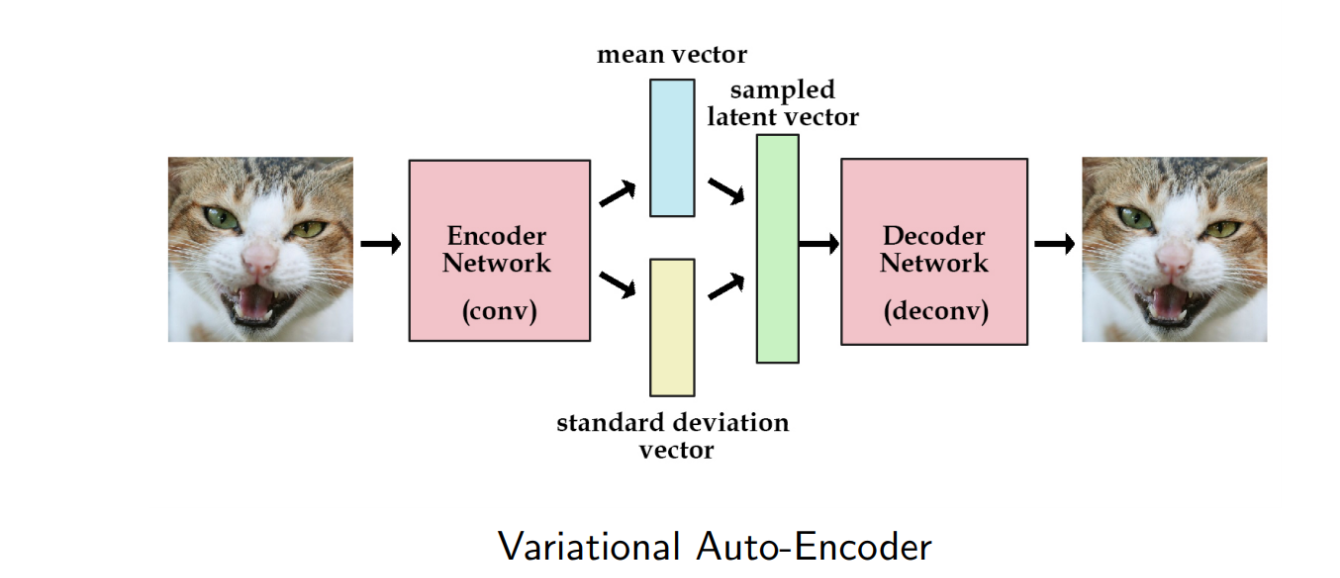
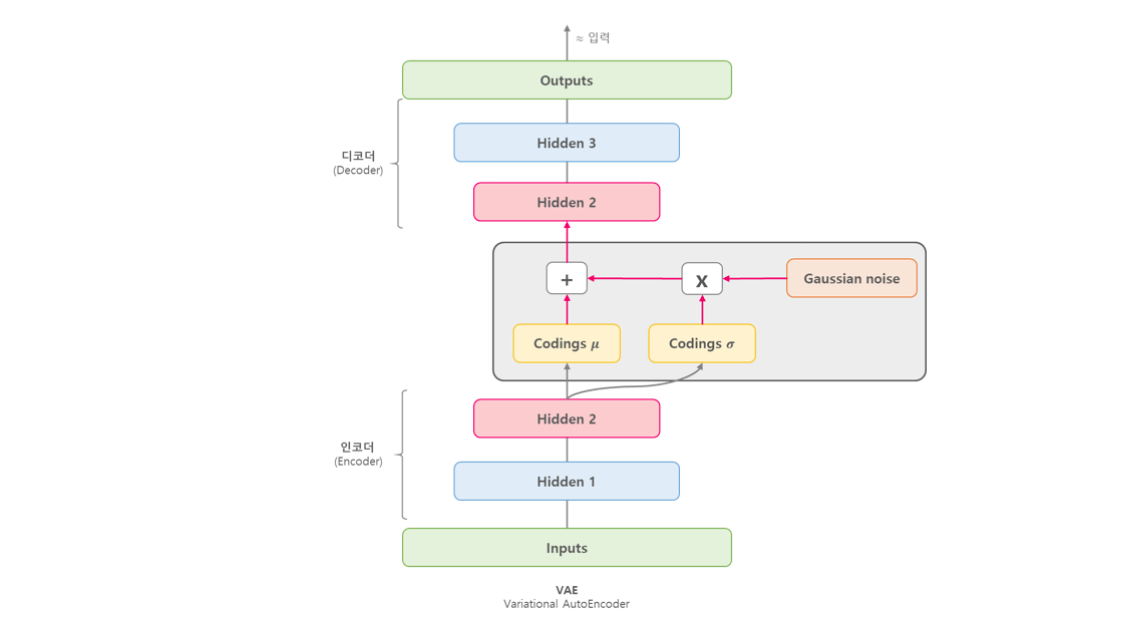
전통적 오토인코더는, 고정된 latent vector로 압축한다. 하지만 VAE는 확률분포로 압축한다.
장점으로 다양한 z를 샘플링하여 새로운 데이터 생성이 가능하고, 데이터 생성과 복원에 강하다.

---

Generative adversarial networks GAN

Generator와 Discriminator가 서로 경쟁(적대적 학습)하면서 데이터를 생성. 생성 모델 G는 실제 데이터의 분포를 학습하여 새로운 데이터를 생성하는 역할이고 판별 모델 D는 입력된 샘플이 실제 데이터셋에서 온 것인지 G가 만든것인지 확률로써 추정한다.

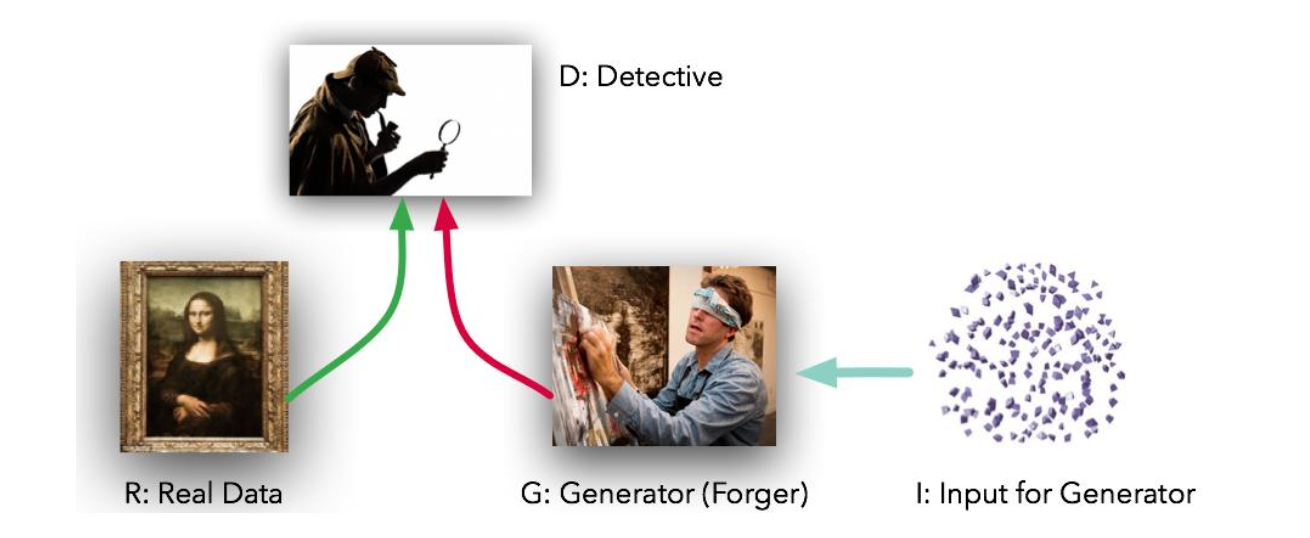
• 생성 모델 : 위조지폐를 만드는 팀이다.
• 판별 모델 : 경찰

두 모델은 경쟁하며 실력(성능)이 좋아진다.

생성 네트워크

생성자의 신경망
GAN에서 가짜 데이터를 만들어내는 부분

• Generator’s distribution $p_g$ over data $x$
  생성자가 만들어내는 데이터 $x$의 확률분포. 즉, 생성자가 학습을 통해 실제 데이터와 비슷한 분포 $p_g(x)$를 만들어내는 것이 목표.

• Prior on input noise: $p_z(z)$
  입력 노이즈 $z$의 사전분포(prior). 보통 표준 정규분포(평균 0, 분산 1)를 사용. 생성자는 이 랜덤한 노이즈 $z$를 받아서 데이터 $x$를 생성.

• MLP: $G(z; \theta_g)$
  다층 퍼셉트론(MLP, Multi-Layer Perceptron) 구조의 생성자 신경망.
  $G$는 생성자 네트워크 함수, $z$는 입력 노이즈, $\theta_g$는 생성자의 파라미터(가중치와 편향 등).
  즉, $G(z; \theta_g)$는 "노이즈 $z$를 받아서 파라미터 $\theta_g$로 데이터 $x$를 생성하는 신경망"을 의미.

판별 네트워크

판별자의 신경망
GAN에서 입력 데이터가 진짜인지 가짜인지 구분하는 역할

• MLP: $D(x; \theta_d)$
  다층 퍼셉트론(MLP, Multi-Layer Perceptron) 구조의 판별자 신경망.
  $D$는 판별자 함수, $x$는 입력 데이터, $\theta_d$는 판별자의 파라미터(가중치, 편향 등).

• Output is a single scalar
  출력은 단일 스칼라 값(0과 1 사이의 확률)로, 입력 $x$가 실제 데이터일 확률을 나타냄.

• $D(x)$: probability that $x$ came from the data rather than $p_g$
  $D(x)$는 입력 $x$가 생성자 분포 $p_g$가 아닌 실제 데이터 분포에서 왔을 확률을 의미함.
  값이 1에 가까우면 진짜 데이터, 0에 가까우면 가짜 데이터(생성자가 만든 것)일 가능성이 높음.

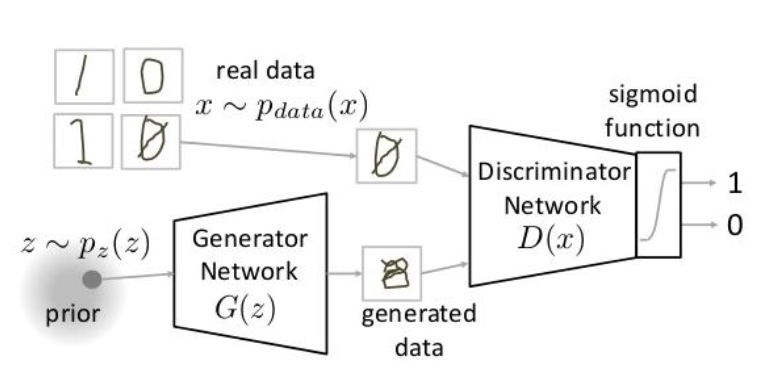
Training

• 판별자 $D$는 진짜 데이터 $x$를 입력받으면 1(진짜), 생성자가 만든 가짜 데이터 $G(z)$를 입력받으면 0(가짜)로 분류하려고 한다.

• $D$의 목표: $D(x)$는 1에 가깝게, $D(G(z))$는 0에 가깝게 만드는 것

• 생성자 $G$는 판별자 $D$가 $G(z)$에 대해 0이 아닌 1에 가깝게 예측하도록(즉, 가짜를 진짜로 속이도록) 학습함.

• 즉, $G$는 $\log(1 - D(G(z)))$를 최소화하려고 함

• $D$는 loss를 최대화(진짜/가짜를 잘 구분), $G$는 loss를 최소화(가짜를 진짜처럼 보이게)

• 두 신경망이 서로 반대 목표를 갖고 경쟁하는 "미니맥스 게임(minimax game)" 구조.

• 아래 수식은 GAN의 표준 손실 함수(미니맥스 손실)

• 첫 번째 항: 진짜 데이터 $x$에 대해 $D(x)$가 1(진짜)에 가깝게 예측되도록 학습.
• 두 번째 항: 가짜 데이터 $G(z)$에 대해 $D(G(z))$가 0(가짜)에 가깝게 예측되도록 학습.
• $D$는 전체 값을 최대화, $G$는 전체 값을 최소화(즉, $D$를 속이려고 함)[2][3][6].

$\mathbb{E}_{x \sim p_{\text{data}}(x)} [\log D(x)]$에서

• $\mathbb{E}$는 "기댓값(average, expectation)"을 의미함.
• $x \sim p_{\text{data}}(x)$는 "실제 데이터 분포 $p_{\text{data}}(x)$에서 샘플링한 $x$"라는 뜻.
• 즉, "실제 데이터셋에서 여러 $x$를 뽑아서, 그 $x$에 대해 $\log D(x)$의 평균(기댓값)을 구한다"는 의미.

---

A rough graphical example

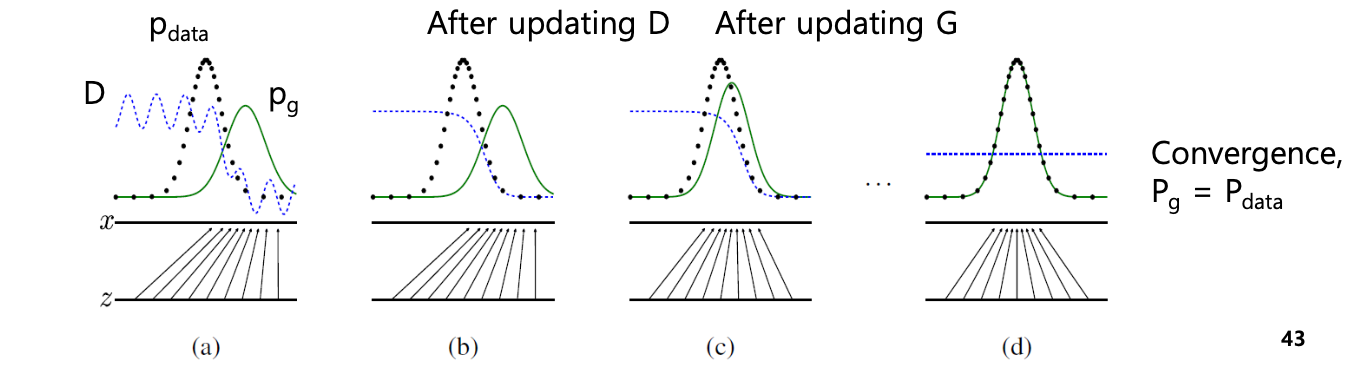
검은색은 원래의 데이터 분포, Generator로 들어감
G는 해당 데이터를 받아 초록색 선을 출력

파란색 직선은 D의 출력
pdata -> 1
pg -> 0 으로 판단.
분포가 다를 때

계속해서 G,D를 학습하면
G가 D를 따라감.
D가 잘 분류하면 이거를 속이기 위하여 G가 p data를 따라가게끔 학습.

Conditional vs Uncoditional

비조건부 GAN

• 랜덤 노이즈만 입력으로 받아 출력을 생성함
  
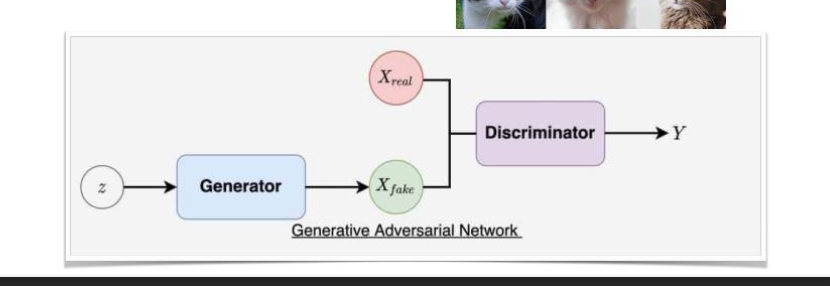
  생성자는 오직 랜덤노이즈만 입력으로 받아 데이터를 생성한다. 생성된 데이터가 어떤 클래스에 속하는지는 제어할 수 없고, 무작위로 다양한 데이터를 만들어낸다.

조건부 GAN

• D와 G 모두 주어진 조건에 따라 행동함.
  
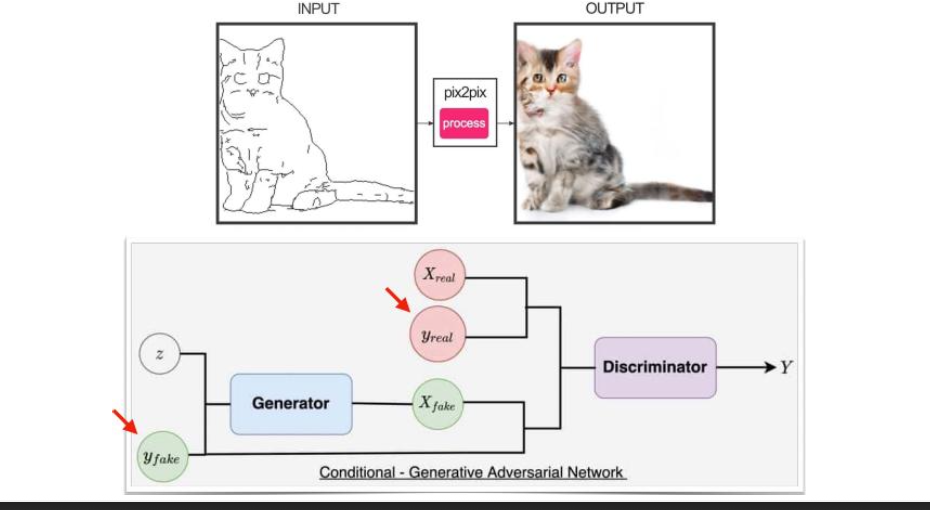
  레이블 같은 추가 조건을 받음.
  이를 통하여 원하는 클래스를 지정 후 그에 맞는 데이터를 생성할 수 있다.

문제점

G는 D를 속이기 위해 실제 데이터를 따라가기보다 단순히 D를 잘 속이는 방향으로 학습
D도 G와 실제 데이터를 구분해야 하는 쪽으로 학습되어야 하는데, G가 만든 데이터의 특징을 파악하여 해당 데이터만 잘 찾아내는 쪽으로 학습됨.

-> 조건부 GAN으로 해결

---

Diffusion Models

Denoising diffusion probabilistic models DDPM

순방향 : 입력 데이터에 점진적으로 노이즈 추가
역방향 : revserse denoising, 노이즈를 제거하면서 데이터 생성

GAN과 달리 데이터 분포를 가우시안 노이즈로 변환했다가 다시 복원하는 점진적 생성 과정

마코프 체인 어쩌구 저쩌구

DDPM은 데이터 분포와 노이즈 분포 사이의 명확한 전환 과정을 정의함.

---

주요 요소	Generative Adversarial Networks (GAN)	Denoising Diffusion Models (DDPM)	Variational Autoencoders, Normalizing Flows (VAE/NF)
High Quality Samples	O (고품질 샘플)	O (고품질 샘플)
Fast Sampling	O (빠른 샘플링)		O (빠른 샘플링)
Mode Coverage/Diversity		O (다양한 분포/모드 커버리지)	O (다양한 분포/모드 커버리지)
비고		Requires ~1K network evaluations! (샘플 하나 생성 시 약 1,000회 네트워크 평가 필요)