자꾸 미루어서 일단 만들었다. 내일부터 꼭 채우자 😎 꼭... 블록체인도 마저 채워넣구...
넣을 것 + linar regression R² 과 correlation coefficient의 관계
https://stats.stackexchange.com/questions/83347/relationship-between-r2-and-correlation-coefficient
2022-10-17
R² = correlation coeff²?
(통계는 왜 매번 새로울까...)
linear regression을 수행하면 나오는 결정계수 R²은 correlation coefficient의 제곱과 같다는 설명을 보았다. 이걸 보고 든 생각은 (1) 왜 linear regression 성능 따지는 데 correlation이 튀어나오지? (2) 그러면 왜 처음부터 correlation coeff라고 안 하는거지? 였다.
좀 더 찾아보니 둘이 같다는 글도 있고, 다르다는 글도 있어서 하나씩 읽어보려고 한다.
우선 오늘은 R²의 의미부터!
R² 의미
(출처: 블로그 글)
linear regression으로 구한 가 있다고 할 때, 로 표현할 수 있다. 이 때 좌변을 의 형식으로 맞추면 좌변은 의 편차가 된다. 우변도 좌변에 맞게 처리를 거치면 , 가 된다. 첫 번째 항은 추정치로 인해 발생한 편차이고, 두 번째 항은 오류항으로 인해 발생한 편차이다.
양변에 제곱을 취하면 좌변은 "의 변동(SST, Total Sum of Square)"이고 우변은 "회귀식으로 설명 가능한 변동(SSR, Regression Sum of Square)"과 "회귀식으로 설명 불가능한 변동(SSE, Error Sum of Squares)"의 합이다.
즉 로 정리할 수 있다.
"회귀식이 얼마나 실제 데이터를 잘 모사하는지"를 표현하는 설명계수 R²은 다음과 같다.
, 즉 회귀선으로 인한 오차가 하나도 없다면 이니까 R²은 1이다. 반대의 경우 0이 된다.
선형 회귀에서 R²=1 이라면 correlation coeff도 1이 될 가능성이 높다는 것은 어렴풋이 추정할 수 있다. R²과 correlation coeff가 동일한 것인지는 다음에 이어서 확인한다!
2022-10-18
Pycharm setting Intepreter with conda env
(파이참에서 기존에 세팅한 인터프리터를 못 찾아서 나중을 위해 적어둠)
1. Intepreter settings-show all intepreter로 들어가면 기존에 세팅한 인터프리터가 나온다.
2. 아예 새로 추가해야 하는데 Add Interpreter가 가상환경 인터프리터를 인식하지 못하면 Add Intepreter-Conda Env 메뉴에서 Interprete=C:\Users\계정명\anaconda3\envs\프로젝트명\ python.exe, Conta excutable=C:\Users\계정명\anaconda3\Scripts\conda.exe (디폴트 값 그대로)를 그대로 넣으면 된다.
class로 전역변수 제거
원래 이런 모양의 코드였는데
var1 = 1
var2 = func2()
def func1():
var3 = var1 + ...
#...
def func2():
func1()
#...별도의 main 없이 돌아가는 이 코드를 외부에서 실행해야 해서 부득이하게 전부 하나의 main 함수 안으로 밀어넣어야 했다. 이렇게 했더니 전역변수로 세팅한 var1이 함수에 들어가지 않는 문제가 발생...
class something(object):
def __init__(self):
self.var1 = 1
self.var2 = self.func2()
def func1(self):
var3 = self.var1 + ...
#...
def func2(self):
self.func1()
#...전역변수 대신 클래스 변수를 쓰는 형태로 바꾸었다! __init__ 내에서 메서드 func2를 불러올 수 있다는 것도 새로 알았다. (순서랑 상관있을 줄...)
(그런데 클래스 밖에서 정의한 함수도 메서드에서 불러오는 게 가능한 것 같은데... 실험해봐야겠다.)
2022-10-19
선형회귀 결정계수 = 상관계수² 성립조건
출처 1 ( 유도)
출처 2 (최소자승법 선형회귀 결정계수 = 상관계수² 증명)
출처 3 (등식 성립 조건)
선형회귀 결정계수가 상관계수의 제곱과 같다는 등식은 최소자승법으로 구한 선형회귀일 때 성립한다.
이틀 전에 본 로 결정계수를 정의하면 결정계수와 상관계수의 제곱이 같은 것이 맞다. 다만 이 수식 자체가 최소자승법을 가정한 것이다.
위 수식을 유도하는 과정에서 아래 식이 나온다.
이 때 좌변이 SST, 우변의 첫 번째 항이 SSR, 두 번째 항이 SSE이다. 즉 이 나오려면 우변의 마지막 항이 0이 되어야 한다. 이 때 최소자승법을 가정하면 마지막 항이 0이 되고 위의 등식이 성립한다.
따라서 항상 선형회귀의 결정계수가 상관계수의 제곱이라고 말할 수는 없다. (대부분 최소자승법을 사용하기 때문에 이렇게 표현하는 것 같다)
2022-10-20
ACF confidence interval ~ Standard Error
강의에서 통계학보다 파이썬 사용법 위주로 알려주어서 아쉽다 ㅠㅜ
ACF에서 신뢰구간 구하는 식인 이 어떻게 나온건지 궁금해졌다. Standard Error () 에서 표준편차 로 두고 나온 것처럼 보이는데(매틀랩도 White Noise에서 ACF 신뢰구간이라고 설명함) 음... Standard Error가 뭔지 알아야 ACF 신뢰구간도 이해가 가겠다.
Standard Error
출처 1 SE 정의
출처 2 왜 으로 나누나요? (아직 못읽음)
모집단에서 추출한 표본집단의 통계치(예: 평균)의 표준편차. 예를 들어 모집단에서 표본집단 100개를 만들고 각각의 평균값 100개를 구했을 때, 100개의 평균값의 표준편차를 Standard Error라고 부른다.
모집단의 표준편차가 크면 클수록 표본집단의 통계치의 표준편차도 커지기 때문에, SE는 모집단의 표준편차 에 비례한다. 그리고 모집단의 사이즈가 클수록 통계치가 실제의 통계치와 유사해지기 때문에 모집단의 샘플 사이즈 에 반비례한다.
White Noise의 ACF 신뢰구간이 SE랑 동일하다는 얘기가 되는데 특정 증명(?)에서 그렇다고만 나오고 더 설명이 나온 건 없어보인다. 예전에 같은 걸로 찾아볼 때에도 없어서 그냥 받아들이고 넘어갔던 것 같다...
2022-10-21
Stationarity 정상성
- Strong stationarity: 데이터의 분포가 시간에 의존하지 않는다.
- Weak stationarity: 데이터의 평균, 분산, 자기상관이 시간에 의존하지 않는다.
정상성을 보는 이유는 예측 모델의 parameter를 구할 때 데이터가 stationary하면 추정하는 parameter의 개수가 줄어들기 때문이다.
trend 혹은 seasonality가 강한 데이터는 평균값 등이 시간에 의존하므로(trend: 평균이 시간이 지날수록 커짐, seasonality: 평균이 특정 주기마다 커지거나 작아짐) nonstationary하다.
nonstationary한 데이터를 stationary하게 만드는 대표적인 방법이 과 같이 차분을 구하는 것이다. 주기가 m의 간격으로 나타나는 데이터라면 으로 차분을 할 수 있다. 파이썬 df에서는 df.diff(m)을 사용한다.
(석사 때 seasonality 제거 방법으로 m의 주기로 평균값을 구해서 그 값을 m번째 값마다 빼는 방식을 썼는데 이런 방식도 있었군 😮 신기)
2022-10-22
AR Model 정의
여기서 는 평균, 은 노이즈, 는 AR parameter를 의미한다. 위 수식을 만족하는 모델이 Auto-Regressive Model이다. m에 따라 m차 AR 모델이라고 부른다.
AR(1) Model 성질
- 이면 Random Walk 모델과 같다.
- 이면 정상성을 가진다.
- 이면 mean reversion이다(금융 용어). 즉 가 로 회귀하려는 성질을 가진다.
- 이면 momentum이다(금융 용어). 즉 가 이전 time step의 값에 관성을 가진다.
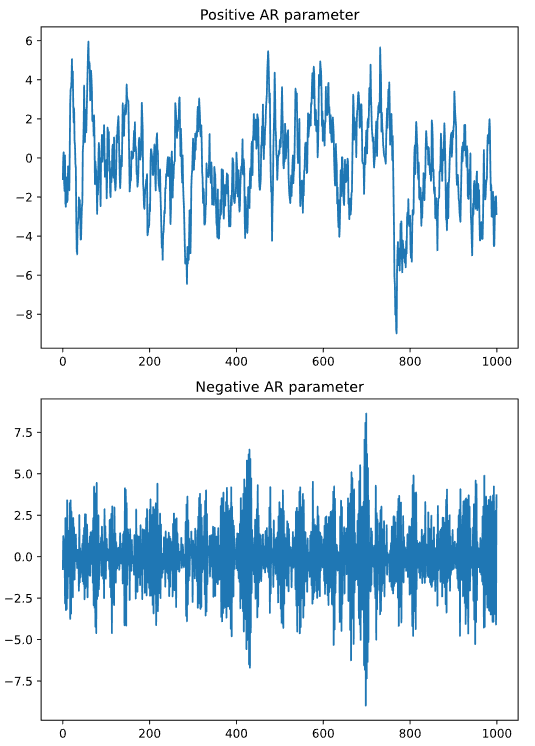
- 이면 Autocorrelation Function이 time lag에 따라 correlation이 교차로 발생한다. 이전 time step과 음의 상관을 가지기 때문에 당연한 결과.
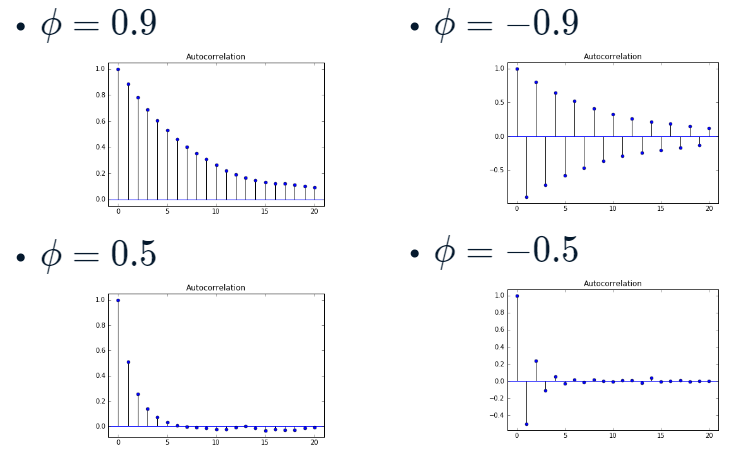
출처: DataCamp
AR Model 차수 정하기
AR 모델의 차수를 정할 때 아래 두 가지 정보를 사용할 수 있다.
- Partial Autocorrelation
- Information Criteria
첫째, Partial Autocorrelation
Partial Autocorrelation은 일정 lag를 가진 데이터 간의 자기상관을 구할 때, 그 사이의 (1~lag-1) 데이터의 효과를 제거하는 방식이다.
그리고 이 Partial Autocorrelation coefficient는 정의상 AR Model의 parameter 와 일치한다.
그래서 Partial Autocorrelation coefficient가 유의한 최대 time lag를 AR 차수로 보면 된다.
둘째, Information Criteria
모델의 parameter(여기서는 AR Model의 차수)는 많을수록 데이터에 잘 맞지만 동시에 과적합의 위험도 가져온다. 모델이 과적합되었는지 판단하는 방법이 Information Criteria 이다.
parameter의 수에 따라 패널티를 부과하여 모델을 만들어 모델이 적합하게 fit 되었는지 판단하는 방식이다. 이 값이 낮을수록 적합하게 fit 되었다고 본다. 가장 많이 쓰이는 Information Criteria는 (1) AIC (Akaike), BIC (Bayesian) 이다.
데이터를 AR Model에 fitting하면 여러 차수의 AR Model을 생성하는데, 이 때 가장 낮은 AIC와 BIC를 가지는 차수를 AR Model의 차수로 선택한다. 아래 그림에서는 AR(3)가 가장 적합함을 알 수 있다.
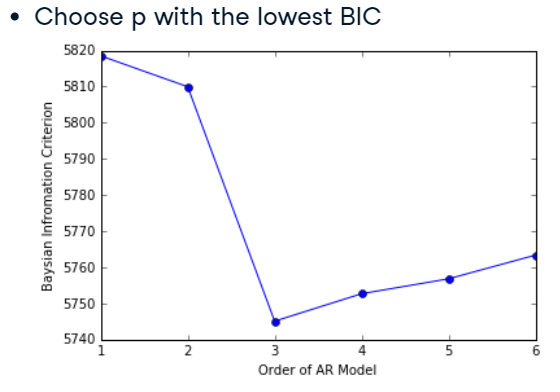
출처: DataCamp
아래와 같이 테스트로 만든 모델의 AIC를 출력해서 비교할 수도 있다.
from statsmodels.tsa.arima.model import ARIMA
# Fit the data to an AR(1) model and print AIC:
mod_ar1 = ARIMA(my_data, order=(1, 0, 0))
res_ar1 = mod_ar1.fit()
print("The AIC for an AR(1) is: ", res_ar1.aic)
# Fit the data to an AR(2) model and print AIC:
mod_ar2 = ARIMA(my_data, order=(2, 0, 0))
res_ar2 = mod_ar2.fit()
print("The AIC for an AR(2) is: ", res_ar2.aic)아래는 위 코드의 결과이다. AR(2)가 더 적합하다.
<script.py> output:
The AIC for an AR(1) is: 510.534689873311
The AIC for an AR(2) is: 501.92741234091392022-10-24
밤이 늦어 오늘은 복습만 😪
Random Walk 정의
이면 random walk, 이면 drifted random walk 라고 한다.
스터디 시간에 random walk와 drifted random walk의 차이점으로 시간에 따른 분산의 변화(전자는 증가/후자는 유지), 평균값의 변화(전자는 유지/후자는 증가)가 언급되었는데 왜 그렇게 되는지는 아직 확실하지가 않다.
2022-10-25
MA Model
AR과 마찬가지로 는 평균, 은 노이즈이고, 는 MA parameter이다. m에 따라 m차 MA 모델이라고 부른다.
MA(1) Model 성질
- 이면 White noise와 같다.
- 모든 에 대해 정상성을 가진다.
- AR과 마찬가지로 이면 mean reversion, 이면 momentum이다.
이 식의 증명은 이 블로그 참조.
2022-10-26
ARIMA
statsmodels 패키지의 ARIMA는 AR, MA, 둘을 혼합한 ARMA, 그 외(ARIMA, SARIMA) 모델을 fitting할 수 있는 클래스이다.
ARMA 클래스가 받는 파라미터인 order = (p, d, q)는 세 개의 값을 가진 튜플이다. 여기서 p는 AR의 차수, d는 차분의 차수, q는 MA의 차수이다. 그 외에도 여러 파라미터가 있지만 강의에서는 이 파라미터만 다룬다.
AR & MA estimation with ARIMA
시계열 data에 ARMA 모델을 fitting 하는 방법은 다음과 같다.
from statsmodels.tsa.arima.model import ARIMA
mod = ARIMA(data, order=[1, 0, 1]) # 1차 ARMA, 차분 없음
# mod = ARIMA(data, order=[1, 0, 0]) # 1차 AR, 차분 없음
# mod = ARIMA(data, order=[0, 0, 1]) # 1차 MA, 차분 없음
res = mod.fit()
print(res.summary())ARMA의 fit summary 출력 결과는 다음과 같다.
const coef는 , ar.L1 coef은 1차 AR parameter ,
ma.L1 coef는 이다.
SARIMAX Results
==============================================================================
Dep. Variable: y No. Observations: 1000
Model: ARIMA(1, 0, 1) Log Likelihood -1420.196
Date: Wed, 26 Oct 2022 AIC 2848.391
Time: 16:45:53 BIC 2868.022
Sample: 0 HQIC 2855.852
- 1000
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const -0.0038 0.003 -1.196 0.232 -0.010 0.002
ar.L1 0.0277 0.037 0.756 0.449 -0.044 0.099
ma.L1 -0.9025 0.015 -60.721 0.000 -0.932 -0.873
sigma2 1.0009 0.045 22.237 0.000 0.913 1.089
===================================================================================
Ljung-Box (L1) (Q): 0.00 Jarque-Bera (JB): 0.13
Prob(Q): 0.99 Prob(JB): 0.94
Heteroskedasticity (H): 1.00 Skew: -0.03
Prob(H) (two-sided): 1.00 Kurtosis: 2.98
===================================================================================AR & MA forecasting with ARIMA
fitting한 모델로 이후 시간의 예측값을 얻으려면 plot_predict를 사용해야 한다.
ARIMA 클래스를 이용해 fitting을 마친 후, 그 모델을 plot_predict에 전달해 예측한다. 파라미터 start와 end는 예측 시작과 종료 time step이다.
MA 모델의 경우 차수만큼의 time step이 지난 다음에는 이후 값이 동일하다. 그 이유는 MA 식에서 차수 다음 스텝의 값을 예측할 때 에 White noise의 기대값 를 대입하기 때문이다. 이므로 가 된다.
...고 스택에서 설명 하는데 이해가 잘 안 된다. 이건 스터디 방에 물어봐야겠다...
from statsmodels.tsa.arima.model import ARIMA
from statsmodels.graphics.tsaplots import plot_predict
mod = ARIMA(data, order=[1, 0, 0]) # 1차 AR
res = mod.fit()
fig, ax = plt.subplots()
data.loc[950:].plot(ax=ax) # 기존 데이터 플롯
plot_predict(res, start=1000, end=1010, ax=ax) # 모델로 예측한 데이터 플롯
plt.title('Data and Forcasted Data with AR(1) Model')
plt.show()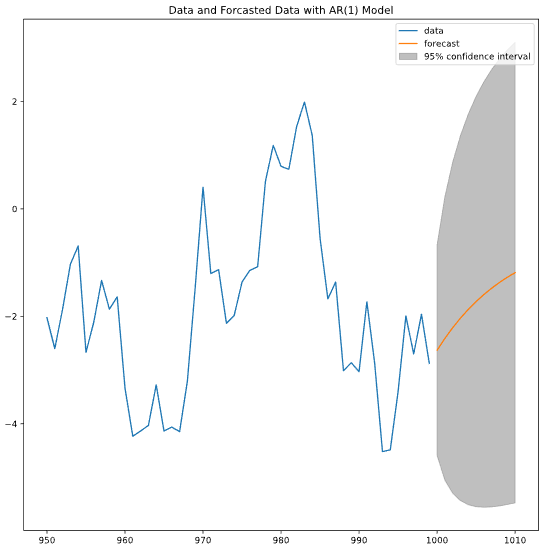
2022-10-30
Cointegration Models
서로 다른 Random Walk 시리즈 와 의 선형 조합 는 Random Walk가 아닐 수 있다.
따라서 Random Walk인 시리즈는 예측할 수 없지만, 이들의 선형 조합은 예측 가능하다. 이 때 와 를 Cointegration(공적분)이라고 부른다.
(이게 무슨 소리인가 싶어 본 예시)
1. 천연가스와 난방용 기름 가격은 각각 Random Walk이지만, 둘의 선형 조합은 평균값을 돌아가려는 성질(mean reverting)을 가진다.
2. 대체제에서 이런 성질을 많이 보이지만 두 시리즈가 경쟁 관계라고 해서 반드시 Cointegration인 것은 아니다.
Test for Cointegration Models
- 를 에 선형회귀하여 선형회귀 계수 를 구한다.
- 에 Random Walk 테스트인 Augmented Dickey-Fuller 테스트를 수행한다.
- 2의 결과가 Random Walk가 아니라면 와 는 Cointegration이다.
Cointegration 테스트는 아래 코드로 수행할 수 있다.
from statsmodels.tsa.stattools import coint
coint(P,Q)2022-10-31
머신러닝 파트로 넘어왔다! (이래도 되는가) 다음 주는 내가 발표이니까 좀 더 열심히 보자 🤗
Machine Learning 절차
- 데이터 특징 추출(Feature extraction)
- 적합한 모델 피팅(Model fitting)
- 예측 및 모델 검증(Prediction and validation)
scikit-learn 기초 - sampels, features
scikit-learn내 메서드는 대부분(samples, features)의 형식을 가진 데이터를 받는다.samples는 표본 각각,features는 표본으로부터 예측하려는 특성을 의미한다. (samples가 데이터(행)의 개수,features가 데이터 특성(열)의 개수라는 설명을 보았는데... 내가 생각한 것이랑 약간 달라서 이건 계속 강의 들어야 파악이 될 것 같다)- 형식을 맞추기 위해
df.T(전치행렬) 혹은df.reshape(-1, 1).shape등을 사용한다.
예
아래와 같은 데이터프레임data가 있다고 가정하자.
이 때 예측하려는 특성(features)가 'target'이고, 특성을 모의할 수 있는 데이터(samples)를 'petal length (cm)'라고 할 때 아래와 같이 정의한다.
이렇게 하면X와y는 각각 1D array가 된다.X = data[['petal length (cm)']] y = data[['target']]

