2월-3월 TIL

Soo Im·2022년 2월 7일
Data AnalysisRandomforestTILregex
0

일별 TIL 기록

목록 보기
8/20
post-thumbnail

2022-02-06

  1. 추가/삭제 버튼 디자인을 이 사이트를 보고 바꿨다. CSS는 설명이 직관적이라 좋다 :9
  2. 결과 텍스트 디자인이랑 내용을 살짝 수정했다.

2022-02-07

맨 위의 텍스트랑 입력 블록을 모두 grid로 정렬하려고 했는데 이렇게 하려면 입력 블록 안의 모든 요소를 다 별도의 div로 만들어야 한다. 요소를 div로 다 떼어놓으면 블록 한 단위의 의미가 사라져서 득보다 실이 클 것 같아 grid는 포기하고 flex를 선택했다. 이 블로그를 보고 두 속성의 차이를 배웠다!

드디어 JS 미니 프로젝트 종료! 막판에 조금 늘어졌지만 끝낸 내 자신 장하다 🤩

2022-02-15

노코드 모임 + 노션 웨비나(중 일부)를 듣고왔다. 새로 알게 된 걸 적어보면

  1. 마솦 오피스 계정으로 Power Platform을 사용할 수 있다(하지만 Power BI는 따로 결제해야 함).
  2. webflow에서 Memberstack을 로그인 플러그인으로 많이 사용한다.
  3. 노션 플러그인 1) Joey: 설문조사 결과를 노션 데이터베이스로 전달 가능
  4. 노션 플러그인 2) Lottifiles: gif를 노션에 임베드할 수 있다. 원하는 이미지의 oEmbed URL을 노션에 복붙>Create Embed 하면 된다! 제일 자주 쓸 듯.

2022-02-22 🥜

seasonal_decompose가 trend, seasonality를 제거하는 간략한 원리

statsmodels.tsa.seasonal의 seasonal_decompose 매서드를 사용하면 시계열의 계절성, 트렌드, 잔차항을 분리하여 볼 수 있다.

from statsmodels.tsa.seasonal import seasonal_decompose
import pandas as pd

# data를 불러온다.
# data df의 index는 DATETIME 형식이어야 한다. 아닌 경우 파라미터를 따로 지정해야 한다.

decompose_result = seasonal_decompose(data, model="multiplicative")

trend = decompose_result.trend
seasonal = decompose_result.seasonal
residual = decompose_result.resid

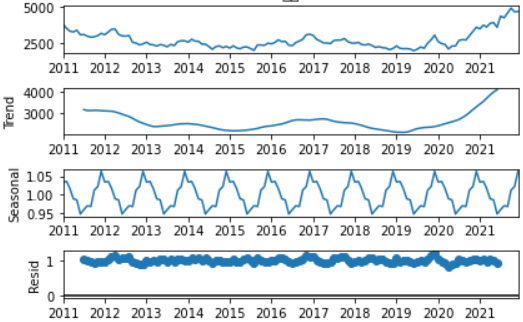
decompose_result.plot();

plot 결과는 아래와 같다. 맨 위가 원본 데이터, 그 아래가 트렌드, 계절성, 잔차항이다.

어떻게 각각을 분리하는 것인지 궁금해져서 몇몇 문서를 찾아보았다. 주로 참고한 자료는 statsmodels.tsa.seasonal 문서, statsmodels.tsa.filters.filtertools 문서, Filtering Time Series 관련 게시글 이다.
아주 정확하지는 않지만 자료를 읽고 내가 이해한 방향대로 정리해보았다.

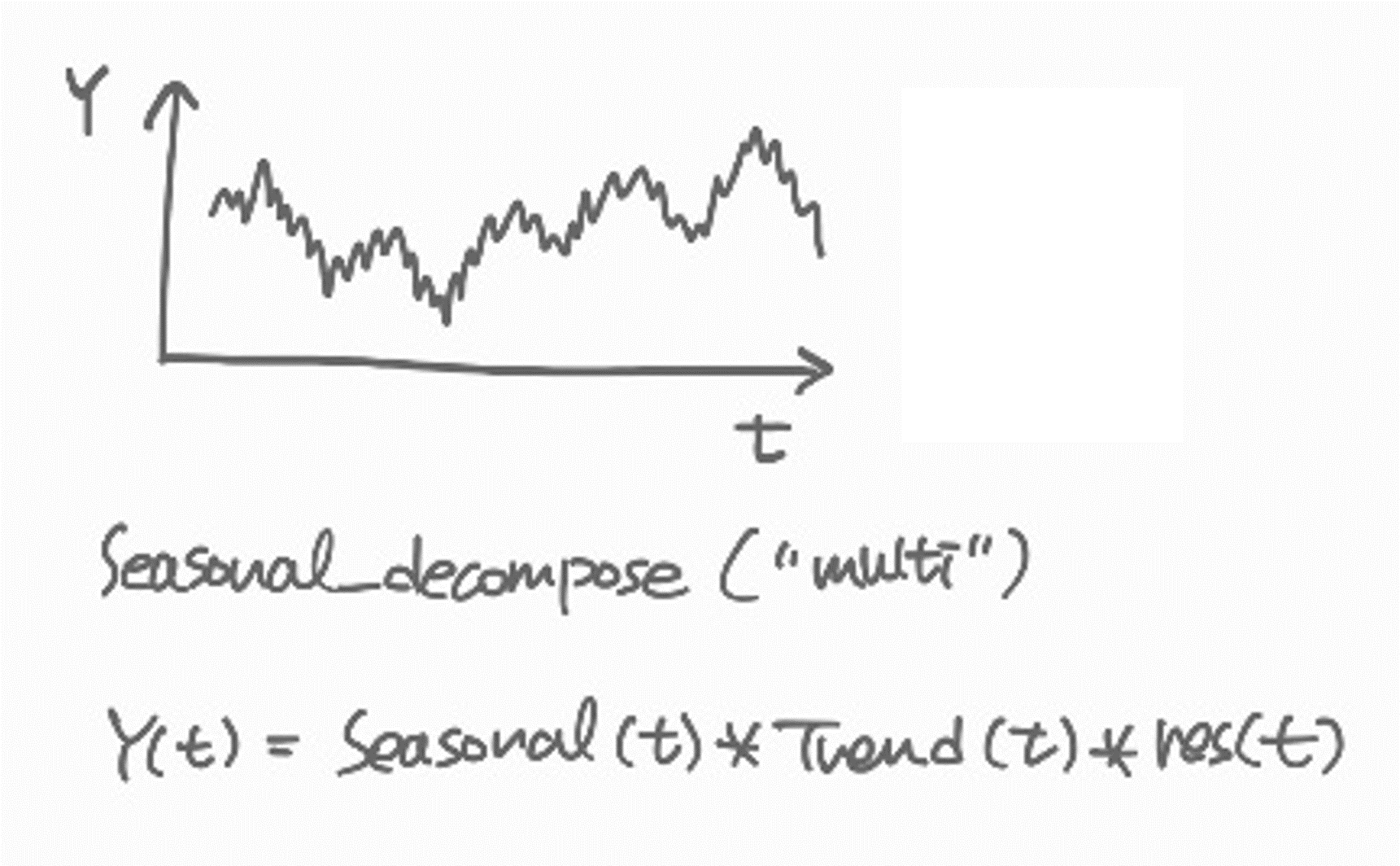
  1. seasonal_decompose는 "additive", "multiplicative" 두 가지 모델을 가지고 있다. 데이터를 trend, seasonality, residual로 분리한다고 가정했을 때 그것들의 합(add)으로 되어있는지, 곱(multipl)으로 되어있는지 선택하는 것이다. 공식 문서에서는 간단히 아래의 식으로 설명한다.
 The additive model is Y[t] = T[t] + S[t] + e[t]

 The multiplicative model is Y[t] = T[t] * S[t] * e[t]

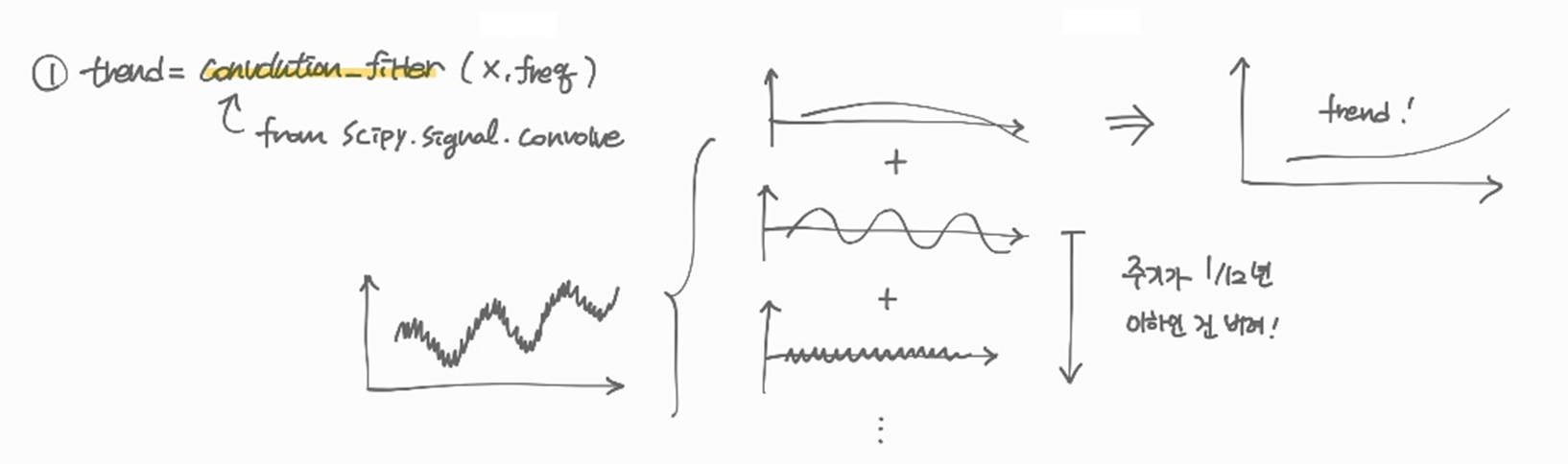
  1. multiplicative 모델을 가정했을 때, 어떻게 각각의 항을 구하는 것일까? 메서드는 가장 먼저 trend부터 구한다. trend = convolution_filter(x, filt) 특정 주파수 이하의 노이즈는 적당히 필터링(filt)해서 구하는 방식이다.
    왼쪽의 데이터를 여러 개의 주기 함수의 합으로 분해한다고 가정해보자. 거대한 상승 흐름은 거대한 주기 함수로 대략 표현할 수 있을 것이고, 아주 세밀한 진동은 작은 주기의 함수로 표현할 수 있다. 이것들을 합치면 원래의 왼쪽 데이터가 나온다.
    convolution_filter는 그 중에서 아주 세밀한 진동은 무시하고 거대한 주기, 즉 거대한 트렌드만을 보겠다는 의미가 된다.
    필터링 기준(filt)는 파라미터를 주지 않으면 원본 데이터의 DATETIME 정보를 보고 메서드가 직접 결정한다. 예를 들어 monthly 데이터는 1개월 미만은 노이즈로 처리해서 제거한다.

  2. 이제 원본 데이터에서 trend를 제거한다. trend를 제거한 데이터에서 계절별(예: monthly의 경우 12회)로 평균을 구하면 계절의 평균값을 구할 수 있다.
    예를 들어 2000년 1월부터 2020년 12월까지 데이터가 있다면 2000년 1월, 2001년 1월, ... 2020년 1월의 평균을 구해 '평균적인' 1월 값을 구한다. 같은 방법을 반복해 '평균적인' 1월부터 12월까지의 값이 나오면 이것이 계절의 평균값이다. 이제 이걸 21회 반복시키면 데이터의 seasonality(혹은 period)가 나온다.

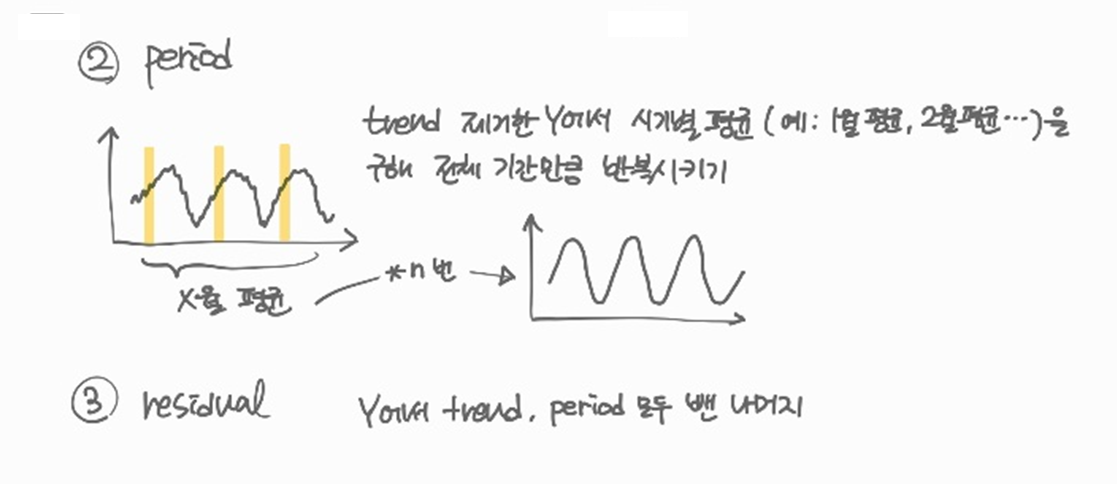
  3. 마지막으로 trend와 period를 모두 원본 데이터에서 제거하면 residual만 남는다.

2022-02-23

Random Forest Regression for (AutoCorrelated) Time Series

RF 모형은 외삽을 위한 모형이 아니기 때문에, 관측하지 못한 값을 예측할 수는 없다. 무한히 먼 미래의 값을 끊임없이 예측하려면 linear regression이 더 나을 수 있다.

하지만 독립변수(X)가 자기상관이 존재하는 상황에서 Xt, Xt-1, Xt-2...를 이용한 multiple linear regression은 적절하지 않다. 이 방법은 독립변수간의 공산성이 없음을 가정하는데 X가 자기상관이 있다면 당연히 Xt, Xt-1, Xt-2...의 공산성은 0이 아니다.

이런 문제에서는 RF가 더 자유롭다. RF는 nonlinear 모형이기 때문에, linearity 가정에서 발생하는 자기상관이 예측을 방해할 여지가 낮다.

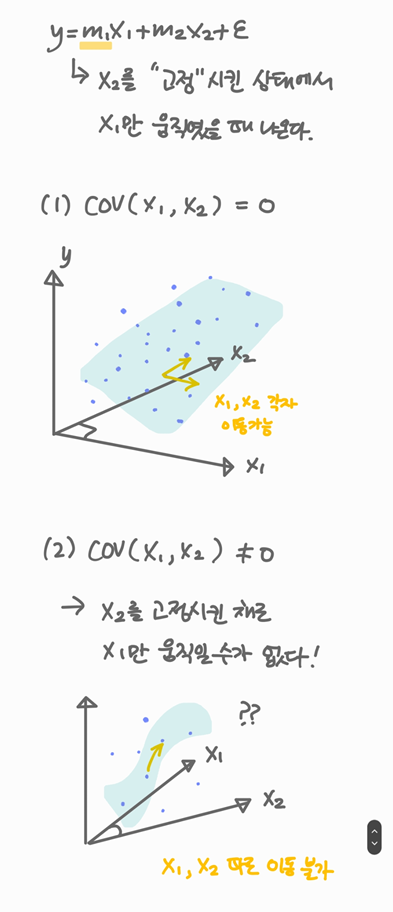
그런데 왜 독립변수끼리 공산성이 없어야 하나? (내맘대로 정리)
Y=m1X1+m2X2+...+mnXn+eY = m_{1}X_{1} + m_{2}X_{2} + ... + m_{n}X_{n}+e 에서 m1,m2...m_{1}, m_{2}...는 각각 다른 독립변수를 고정한 상태에서 해당 변수만 이동하였을 때의 선형회귀 계수이다.
키 X1X_{1}, 독후감 개수 X2X_{2}을 이용해 국어성적 YY를 구한다면 "독후감 개수가 같은 경우 키에 따라 얼마나(m1m_{1}) 국어성적이 바뀌는가?"와 같은 방식으로 구하는 것이다.
그런데 X1X_{1}과 X2X_{2}가 이미 서로 연관이 높은 상태라면 사실상 X1X_{1}을 고정한 채로 X2X_{2}의 효과만 고려할 수는 없다. X1X_{1}이 도서관 방문 횟수라면, 도서관 방문 횟수가 바뀌는 시점에 이미 독후감 개수가 영향을 받고 있을 것이다. 따라서 multiple linear regression에서는 독립변수 공산성이 없어야만 계수가 의미가 있다.

2022-02-24

정규식

매번 제대로 이해 못하고 따라치는 게 갑갑해서 책을 빌려왔다! 점프투파이썬!

  1. 문자 클래스 [ ]
    [ ] 사이의 문자와 매칭한다는 의미이다. [abc]와 문자열 appple, banana는 a 혹은 b가 들어있으니 매칭되고, regex는 안 된다.
    -는 문자 사이의 연속된 범위를 나타내고 ^은 매칭되지 않음을 의미한다. [a-c]는 [abc]와 같고, [a-zA-Z]는 모든 알파벳을 의미한다. [^0-9]는 숫자가 아닌 문자를 의미한다.
    알파벳, 숫자 전체를 가리키는 정규식은 [a-zA-Z0-9_] 또는 [\w]이고, 이들을 제외하는 정규식은 [^a-zA-Z0-9_] 혹은 [\W]이다(참고로 마지막의 _는 특별한 의미를 가지는 것이 아니고 말그대로 문자열에 _가 있는지 확인하는 것이다).
  2. Dot .
    모든 문자를 가리키는 와일드카드. a.b는 aab, a5b와 매칭된다. 다만 앞에서 본 [_]와 마찬가지로 a[.]b는 . 그 자체가 들어가있는지 확인하는 것이다. 그래서 a[.]b는 오로지 a.b 만 매칭된다.
  3. 반복 *, +
    * 앞의 문자가 0번 이상 반복된다는 의미이다. hi*는 h, hi, hiiiii 모두와 매칭된다. +도 비슷하지만 한 번 이상 반복된다는 뜻이다.
  4. 반복 {m,n}
    반복 횟수를 m부터 n까지 제한한다는 의미이다. m, n 중 하나만 쓰는 것도 가능하다. ca{1,2}t는 cat, caat과 매치되고 ca{2}t는 caat, ca{,2}t은 ct, cat, catt와 매치된다. 참고로 {,1}은 ?로도 표현할 수 있다.

2022-03-03

TimeSeriesSplit for Time Series in ML

이전에 쓴 것처럼(02/23) 자기상관이 있는 시계열을 (다른 데이터로부터) 예측하려면 Linear Regression보다 Random Forest를 쓰는 것이 적절하다. 다만 주의할 점은 시계열 자료의 학습셋/테스트셋 분리는 train_test_split이 아닌 TimeSeriesSplit을 사용해야 한다.
이 글에 설명이 정말정말 잘 되어있는데, 간단히 요약하면 다음과 같다.

  1. 시계열 '예측'은 당연히 과거의 데이터만 사용해야 한다.
  2. 1월 5일을 예측하려면 1월 4일까지만 학습셋으로 사용해야 한다. 1월 6일 데이터를 이용해서 1월 5일을 '예측'하는 상황은 현실에서 있을 수 없다.
  3. 문제는 train_test_split을 사용하면 위의 상황이 가능해진다. shuffle = False 옵션으로 뒤죽박죽 섞이는 것을 방지하더라도, 1월 1일, 2일, 4일, 6일이 학습셋으로 들어간다면 5일의 예측 성능은 매우 좋아질 것이다.
  4. 이 현상을 data leakage 라고 부른다. 학습셋에 현실에서 존재할 수 없는 데이터 혹은 테스트셋이 일부 포함된 경우를 말한다(테스트셋 데이터가 학습셋으로 유출되었다는 뜻에서 'leakage'라고 표현한다). 이는 과도한 성능 향상을 가져온다.
  5. 이런 문제를 방지하려면 예측 시점보다 과거의 데이터만 학습셋으로 만들어주는 TimeSeriesSplit을 사용하면 된다. 아래 그림 출처는 여기.

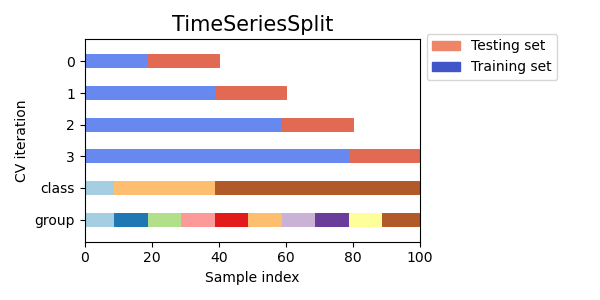
Overfitting vs. Data Leakage
이 글에 잘 설명되어 있다.
Overfitting은 '학습셋'에 과도하게 최적화되어서, '테스트셋'을 넣었을 때 제대로 예측하지 못하는 현상을 말한다.
Data Leakage는 '학습셋'이 '테스트셋'을 일부 포함하고 있어서, '테스트셋'을 넣었을 때 과도하게 예측 성능이 높아지는 현상을 말한다.

2022-03-08

seasonal_decompose결과의 trend, residual NaN처리

statsmodels.tsa.seasonal의 seasonal_decompose를 기본 옵션으로 사용하면 trend와 residual의 앞-뒤 일부가 NaN으로 나오는 것을 볼 수 있다. 아래 그림에서 seasonal은 전체 데이터 타임을 커버하지만 residual은 비어있는 걸 볼 수 있다.

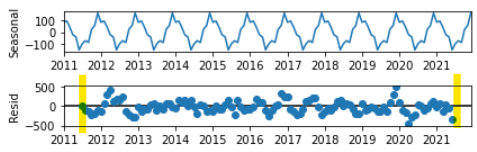
그 이유는 깃허브 이슈에서 볼 수 있었다. seasonal을 구하려면 최소한 한 주기는 있어야 하기 때문에 맨 앞과 뒤의 데이터 중 반 주기는 알 수가 없다. seasonal이 무엇인지 알 수 없으니 trend, residual도 구할 수 없는 것이다.
NaN 대신 임의로 채우려면 extrapolate_trend 옵션을 사용하면 된다. 공식 문서에 따르면 "freq"로 설정할 경우 가장 가까운 포인트, "0이상의 정수"로 설정하면 그 개수만큼의 포인트를 이용해 linear least-squares extrapolated 한다. 아래는 "freq", 정수로 외삽한 예시.

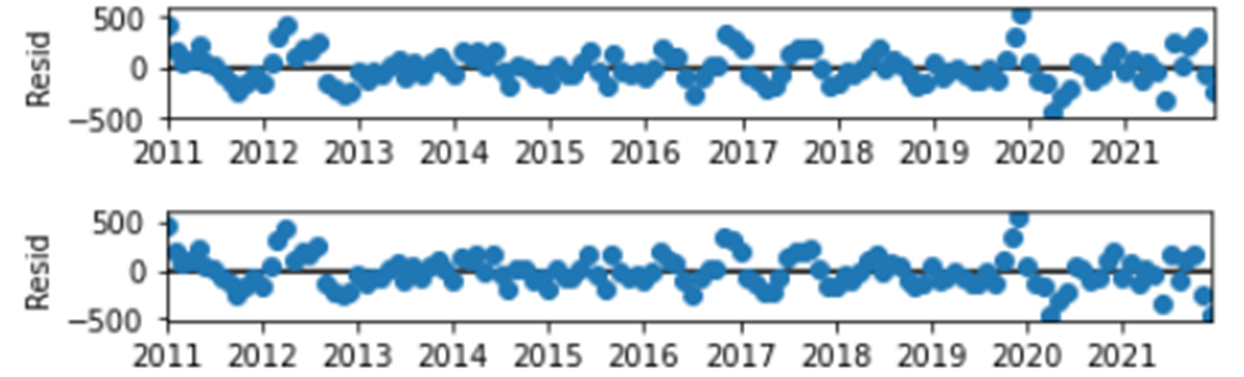
왜 seasonal은 처음/마지막이 NaN이 아닌가?
trend, residual의 앞뒤 반 주기는 날린다는 점에서 "그럼 seasonal도 비어야지 왜 seasonal은 있나?"는 질문이 나올 수 있다. 이건 2월 22일 기록으로 답할 수 있다. seasonal은 하나의 주기를 찾아두고 그걸 데이터 길이만큼 곱한 것이라서 전체 데이터 길이를 커버할 수 있다.

2022-03-10

Seasonality(계절성) vs. Cyclicity(주기성)

Seasonal(Periodic)와 Cyclic은 다른 개념이다!! (기후학에서 seasonal cycle이라고 쓰는데 애초에 둘이 다른 거라 저렇게 썼던 모양이다🙄) 심지어 Periodic이랑 Cyclic은 보통 둘 다 '주기성'이라고 해석해서 더 헷갈린다...
둘을 구분하는 게 중요한 이유는 stationarity(정상성)을 판단하는 중요한 척도이기 때문이다.

시계열이 정상적(stationarity)이다
= 시계열의 특징이 관측 시점과 무관하다
= 시계열의 특징이 시점에 따라 달라지지 않는다
= 일부를 보았을 때 그것을 언제 측정한 것인지 파악할 수 없다

이 조건을 만족하려면 시점에 따라 값의 평균값이 변하거나(trend) 분산이 변하는 등 측정값의 통계값이 변하면 안 된다. 그리고 언제 측정한 것인지 추정이 가능한 계절성도 존재하면 안된다. 즉 정상 시계열은 계절성(seasonality)과 추세(trend)를 가지면 안된다.
반면 주기성(cyclicity)은 정상성에 영향을 주지 않는다. 주기성만으로는 그 데이터가 어느 시점에 측정된 것인지 알 수 없기 때문이다.

그러면 어떤 것이 계절성이고 어떤 것이 주기성일까?
이 글에서는 아래와 같이 설명한다.
계절성은 문자 그대로 계절에 영향을 받는(일/월/연 변화) 패턴으로, 항상 고정된 주기를 가진다. 연 평균 기온은 무조건 1년 주기로 진동을 하기 때문에 계절성을 가진다.
주기성은 고정된 주기가 없는 패턴이다. 경제 사이클은 그것이 위아래로 진동한다는 것은 알지만 사이클이 끝나기 전까지는 그 사이클의 주기를 알 수도 없고, 매번 주기가 다르다.

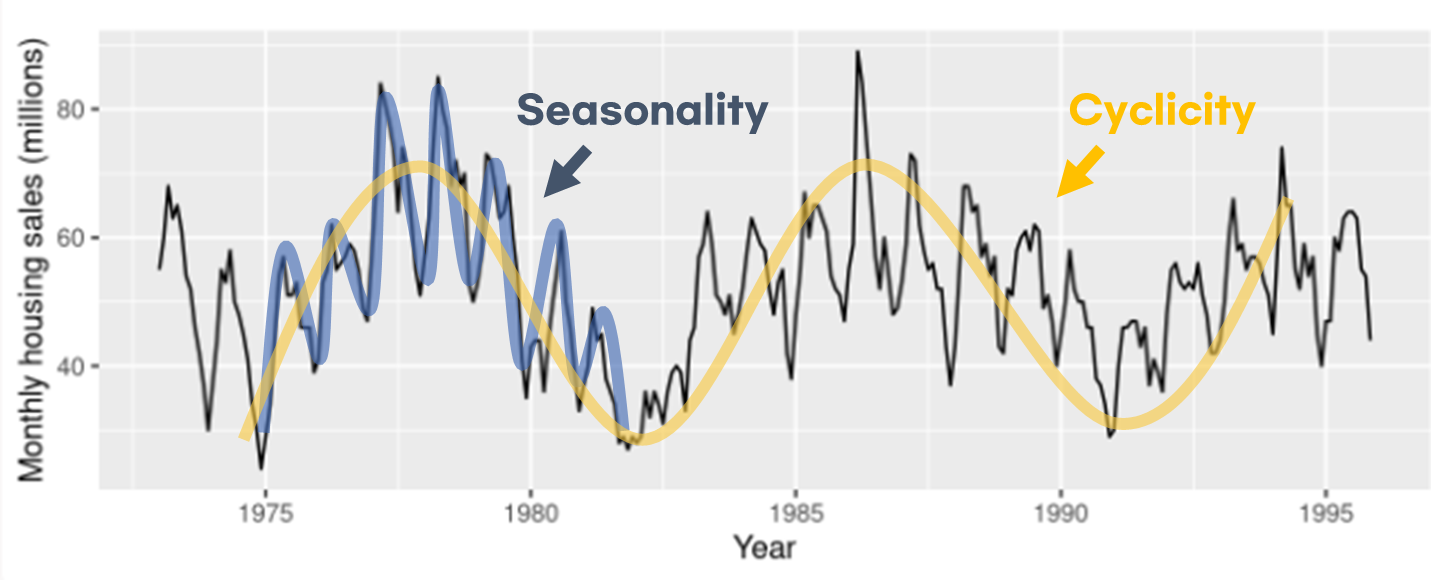
아래 예시는 미국의 신축 단독 주택 월별 판매량(1973-1995)이다(그림 원본 출처).
1년의 고정된 주기로 진동하는 계절성(파란색)과 주기를 정확히 파악할 수 없는 주기성(노란색)이 함께 보인다.

2022-03-21

Moving Average Model 사례

Moving Average Model은 Auto Regressive Model보다 덜 직관적이다. 왜 뜬금없이 에러가 튀어나온거지?

yt=c+εt+θ1εt−1+θ2εt−2+⋯+θqεt−qy_{t} = c + \varepsilon_t + \theta_{1}\varepsilon_{t-1} + \theta_{2}\varepsilon_{t-2} + \dots + \theta_{q}\varepsilon_{t-q}

수식을 풀어서보면
대략적인 값(cc)으로 예측을 해본다. 예측한 값(yt^\hat{y_{t}})이 실제 값(yty_{t})이랑 얼마나 차이(εt\varepsilon_{t})가 나는지 계산해본다. 그리고 다음 값을 예측할 때는 대략적인 값(cc)에 그 전에 발생한 오차(εt−q\varepsilon_{t-q})를 써서 적당히(θt−q\theta_{t-q}) 보정해준다.

그래도 이게 무슨 소리인가 싶다. 여기 유튜브 영상은 주식같은 얘기 없이 아주 직관적으로 잘 설명해준다.

  1. 내가 가엾은 대학원생이라고 생각해보자. 나는 세미나 조교라 주에 한 번 열리는 학과 세미나에서 과자를 준비해야 한다. 학과 사람이 40명이니 40개(cc) 정도 챙겨가면 된다.
  2. 첫 주에는 딱 40개(cc)를 챙겨갔다. 그런데 교수님이 보시고는 "이렇게 모자라게 준비하면 어떡하나? 넉넉히 10개(εt\varepsilon_{t})는 더 챙겨와야지!" 하고 혼내신다. 내가 센스가 없었지. 오병이어를 해서라도 40개(yt^\hat{y_{t}}) 살 돈으로 50개(yty_{t})를 준비해야 했는데.
  3. 한 주가 지나고 나는 고민한다. 당연히 40(cc)개 챙겨가면 혼날거다. 하지만 세미나 준비 비용이 넉넉하지는 않아서 저번 주에 혼난 개수(εt−1\varepsilon_{t-1})의 절반(θt−1\theta_{t-1})만 더 챙기기로 했다. 10/2 = 5니까 45개(yt^=c+θ1εt−1\hat{y_{t}} = c+\theta_{1}\varepsilon_{t-1})를 사갔다.
  4. "왜 과자가 남아도나? 학과 예산으로 자네 과자 사먹는건가? 학생들도 38명(yty_{t}) 뿐인데!" 10개를 더 샀으면 횡령죄로 잡혀갈 뻔 했다. 남는 과자 7개(εt\varepsilon_{t})는 애들이나 나눠줬다.
  5. 넉넉하게도 딱 맞게도 준비할 수가 없다. 생각을 포기하고 지난 주에 모자란 양(εt−1\varepsilon_{t-1})의 절반(θt−1\theta_{t-1})만 반영해 40개(cc)에서 3.5개(θ1εt−1\theta_{1}\varepsilon_{t-1}) 모자라게 챙겼다. 그런데 놀랍게도 이번 주에는 교수님이 오늘의 과자는 딱 맞다고 하셨다! 기준은 알 수 없지만 이번 주 오차(εt\varepsilon_{t})는 0이다!
    ...

이런 식으로 평균 값의 범위(cc, 위에서 40개)에서 지난 번의 오차(εt−q\varepsilon_{t-q})를 적당히(θt−q\theta_{t-q}) 반영하는 방식이 Moving Average Model이다. 여기서 Average는 cc와 같은 의미로, 어쨌거나 저 범위 내에서 값이 변동한다는 의미이다.

2022-03-23

pip vs. pipenv

(노마드코더 에어비앤비 클론 강의 시작!)

패키지를 설치할 때 pip install packagename 으로 설치하는 경우가 많지만 그다지 추천하는 방법은 아니다. pip은 패키지를 global에 설치하기 때문이다. 어떤 프로젝트는 패키지 버전 A를 써야하고 다른 프로젝트는 버전 B를 써야 한다면 pip으로는 불가능하다. global에 설치하는 거니까 둘 중 하나만 가능하다.
대신 pipenv를 사용하면 프로젝트별로 패키지를 따로 설치할 수 있다. 프로젝트별로 서로를 침해하지 않는 일종의 거품(버블)같은 가상환경을 만들어서 그 안에서 패키지를 설치하면 된다.

  1. 프로젝트 디렉토리에서 pipenv --three 명령어를 입력한다. 파이썬 버전3(--three는 파이썬 버전을 의미)로 가상환경이 만들어진다.
  2. 가상환경이 만들어졌으면 해당 디렉토리에 Pipfile이 생성된다.
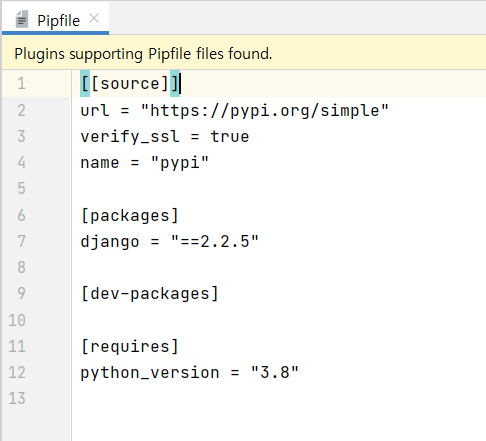
  3. 패키지를 가상환경 '안'에 설치하기 위해 해당 가상환경 안으로 이동해야한다. pipenv shell로 가상환경 내부로 들어간다.
  4. pipenv install packagename으로 원하는 패키지를 설치한다.
  5. 설치가 완료되면 Pipfile에서 내가 설치한 패키지를 확인할 수 있다.

2022-03-24

VSCode로 Django 개발 준비

  1. .gitgnore은 깃헙에 올리고 싶지 않은 파일의 목록을 적어둔 리스트이다. Python gitgnore을 예시로 보면 *.log나 local_settings.py와 같은 파일은 깃헙에 올리지 않는다는 의미이다. 
# Django stuff:
*.log
local_settings.py

  1. (pipenv) Django 프로젝트 세팅하기
    1) 폴더를 생성한다(깃헙도 원하면 세팅).
    2) 폴더 경로에서 pipenv shell 명령어로 가상환경 안으로 들어간다.
    3) django-admin startproject config 명령어로 config 폴더를 만든다.
    4) config 폴더 내부에 config와 기타 파일이 있는데 이것들을 config 폴더 바깥으로 꺼낸다. 이제 비어버린 원래의 config 폴더는 삭제한다.
    5) Ctrl-Shift-P에서 "Python: Select Interpreter" 옵션으로 들어가 현재 디렉토리 내 pipenv를 선택한다.

  2. VSCode 파이썬 개발환경 세팅하기
    1) Extension에서 python을 설치한다(실제 python이 아니고 확장 프로그램임).
    2) 저장하면서 자동으로 python pep(파이썬 코드 작성 규칙) 스타일에 맞춰주는 것을 formatter라고 부른다. formatter에는 여러 종류가 있는데 만약 black을 사용한다면 .vscode 디렉토리 내 settings.json 파일에 아래를 추가한다.
    "python.formatting.provider": "black"
    3) 에러가 날 법한 부분을 미리 찾아주는 것을 linter라고 부른다. flake8을 쓸 경우 마찬가지로 settings.json에 아래를 입력한다.
    "python.linting.flake8Enabled": true, "python.linting.enabled": true
    아니면 Ctrl-Shift-P의 "Python: Select Linter" 옵션에서 flake8을 선택한다.
    4) 위 과정에서 설치가 안 되어있을 경우 우측 하단에 설치 메시지가 나오니 OK 눌러 설치하면 된다. 수동으로 설치할 경우에는 & pipenv install black --dev --pre 와 같이 옵션을 붙여 pipenv 내부에 설치하면 된다.

2022-03-30

ACF vs. PCAF

  1. ACF(Auto-Correlation Function)
    시계열에서 두 시점 간의 상관을 구하는 것이다. 자기 자신Auto)과 상관(Correlation)을 구한다고 해서 ACF라고 부른다. 예를 들어 오늘의 기온은 어제의 기온과 연관이 높으므로 lag = 1day에서 자기상관이 존재하고 ACF 값이 높을 것이다.

  2. PACF(Partial ACF)
    ACF를 'Partial'로 적용한 것이다. ACF가 전미분이라면 PCAF는 편미분에 대응할 수 있다. 오로지 내가 궁금한 것들만 ACF를 수행하는 것이다. 오늘의 기온은 어제의 기온과 연관이 있고, 어제의 기온은 그저께의 기온과 연관이 있다. 그렇다면 오늘의 기온과 어제의 기온의 상관을 구해도 그저께의 기온이 영향을 주었을 것이다. 다른 시점(그제)의 영향을 제외하고 오로지 두 시점(오늘, 어제)간의 상관을 구하는 것이 PACF이다.

ACF->MA, PCAF->AR

  1. PACF -> AR model
    오늘의 기온은 어제의 기온과 유의미한 PCAF를 가지지만 그제와 그 이전의 기온과는 유의미한 PCAF를 가지지 않는다고 가정해보자. 그렇다면 어제의 기온만 가지고도 오늘의 기온을 예측할 수 있을 것이다. 이것이 Auto-Regressive 모델이다. 현재로부터 하나의 시점(어제)만 사용하면 1차 AR 모델, 둘의 시점(어제, 그제)을 사용하면 2차 AR 모델,... 과 같이 부른다.

  2. ACF -> MA model
    아... ACF 차수가 왜 MA로 연결되는지는 아직 이해가 잘 안 간다. 이 영상에서 설명 잘 듣고 있었는데 이 부분에서 막혔다 ㅠㅠ 좀 더 찾아보자...

profile
Soo Im
이전 포스트

1월 TIL 기록

다음 포스트

4월-5월 TIL

0개의 댓글