Programmers | H-Index - Python

soo5717·2021년 5월 4일

1. 개념 정리

1.1 정렬 (Sort)

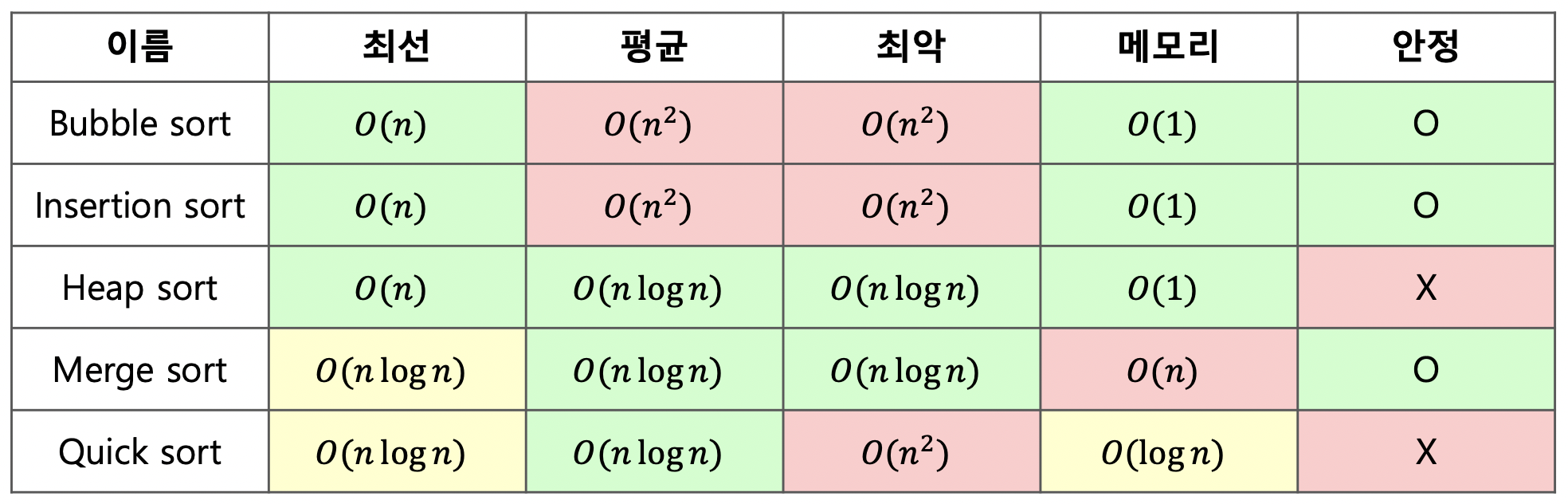
다양한 정렬 알고리즘이 있지만, 대표적인 것은 정렬 알고리즘과 시간 복잡도는 다음과 같다.

파이썬에 내장된 정렬 방식은 Tim Sort 방식을 사용한다.

파이썬에서 리스트를 정렬할 때 가장 간단한 방법은 sort와 sorted 함수를 사용하는 것이다. 두 함수 옵션으로 key를 사용해서 특별한 기준에 따라 정렬도 가능하다.

1.1.1 .sort()

sort 함수는 리스트 내부에 있는 요소들을 정렬해주는 함수이다.

# list.sort() => only list
array = [10, 20, 15, 13, 30, 80, 50]
array.sort() 
print(array) # [10, 13, 15, 20, 30, 50, 80]

array.sort(reverse=True) # 역 정렬

1.1.2 sorted()

sorted 함수는 특정 리스트를 정렬한 후 정렬된 리스트를 반환해주는 함수이다.

# sorted () => iterable
array = [10, 20, 15, 13, 30, 80, 50]
new_array = sorted(array)
print(array) # [10, 20, 15, 13, 30, 80, 50]
print(new_array) # [10, 13, 15, 20, 30, 50, 80]

new_array = sorted(array, reverse=True) # 역 정렬

2. 문제 설명

2.1 H-Index

H-Index는 과학자의 생산성과 영향력을 나타내는 지표입니다. 어느 과학자의 H-Index를 나타내는 값인 h를 구하려고 합니다. 위키백과1에 따르면, H-Index는 다음과 같이 구합니다.

어떤 과학자가 발표한 논문 n편 중, h번 이상 인용된 논문이 h편 이상이고 나머지 논문이 h번 이하 인용되었다면 h의 최댓값이 이 과학자의 H-Index입니다.

어떤 과학자가 발표한 논문의 인용 횟수를 담은 배열 citations가 매개변수로 주어질 때, 이 과학자의 H-Index를 return 하도록 solution 함수를 작성해주세요.

2.2 제한 조건

과학자가 발표한 논문의 수는 1편 이상 1,000편 이하입니다.
논문별 인용 횟수는 0회 이상 10,000회 이하입니다.

2.3 입출력 예시

citations	return
[3, 0, 6, 1, 5]	3

3. 풀이 과정

주어진 조건에 따라서 H-Index를 구하는 문제이다. 초반에는 문제를 이해하기 어렵지만 풀이 자체는 Level 2 문제 중 쉬운 편에 속한다. 하지만 효율까지 고려한다면 다양한 방식으로 풀이가 가능하기 때문에 효율성 검사가 없더라도 신경 써서 문제를 풀면 좋을 것 같다.

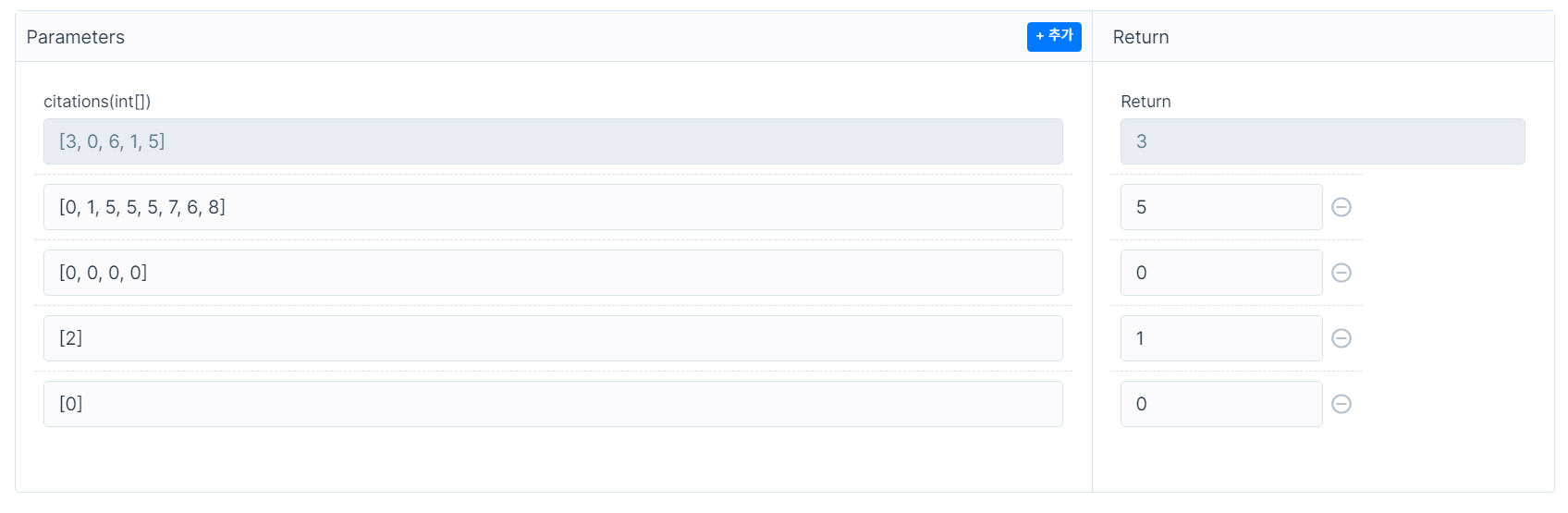
문제를 풀면서 테스트 케이스를 추가해서 풀었었는데, 기존 테스트 케이스로도 충분할 수 있지만 부족하다 느껴지면 다음 테스트 케이스들을 추가해서 풀어보아도 좋을 것 같다.

3.1 역정렬과 반복문 중첩 : 성공😋

직접 생각해낸 풀이 방식이다. H-Index의 범위는 n 이하에 존재한다는 것을 파악 후 n ~ 0까지 거꾸로 순회하면서, h번 이상 인용된 논문의 수가 h편 이상이고 나머지 논문의 수가 h번 이하로 인용되었을 때를 찾아서 해당 h를 반환하는 방식이다.

citations를 역 정렬 한다. (거꾸로 순회하면서 h번 이상 인용된 논문의 수를 세기 위함.)

n ~ 0을 순회한다.

역 정렬된 citations를 순회하면서 h번 이상 인용된 논문의 수를 센다.

인용 횟수보다 h가 더 큰 경우 반복문을 빠져나간다.

앞서 계산한 h번 이상 인용된 논문의 수(count)가 h편 이상이고, 그 외 논문의 수(n - count)가 h편 이하일 경우 h를 반환한다.

이해하기 쉬운 방법이고 문제 그대로의 직관적인 풀이 방식이지만 반복문을 중첩해서 사용했기 때문에 시간 복잡도를 대략 계산해보면 O(n*n)이 나온다.

전체 코드 (python)

def solution(citations):
    citations.sort(reverse = True)
    
    n = len(citations)
    for h in range(n, -1, -1):
        count = 0
        for citation in citations:
            if h > citation: 
                break
            count += 1
        
        if count >= h and h >= n - count:
            return h

실행 결과

3.2 정렬과 반복문 : 성공😋

프로그래머스 풀이를 참고해서 작성해본 코드이다. 문제 난이도가 쉬웠던만큼 다른 사람들의 풀이를 살펴보았을 때 정말 다양한 풀이를 볼 수 있었다. 그중 가장 심플하면서 성능도 좋은 코드에 대해 설명해보고자 한다. 기존의 풀이는 정렬을 제외했을 때 O(n*n)의 시간 복잡도가 나오는데, 이번 풀이는 정렬을 제외하고 O(n)의 시간 복잡도라 더 효율적인 것을 알 수 있다.

citations를 정렬한다.

citations를 순회한다.

citation이 n - i 보다 크거나 같을 경우 n - i가 H-Inex가 되기 때문에 결과를 반환한다.

이전 반복문에서 결과를 반환하지 못했을 경우를 고려해 0을 반환한다.

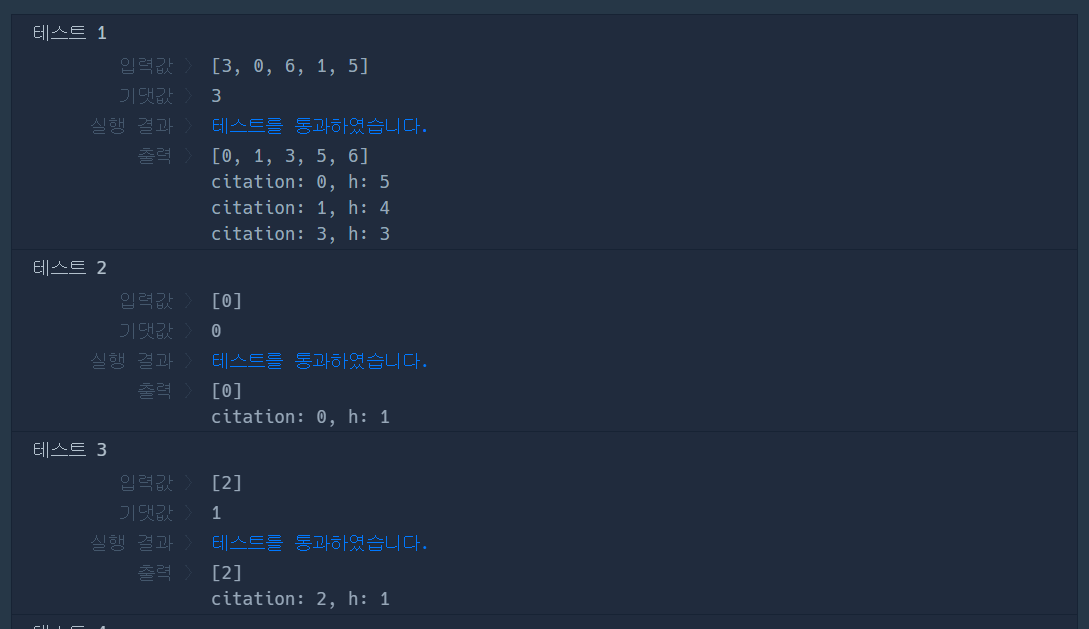
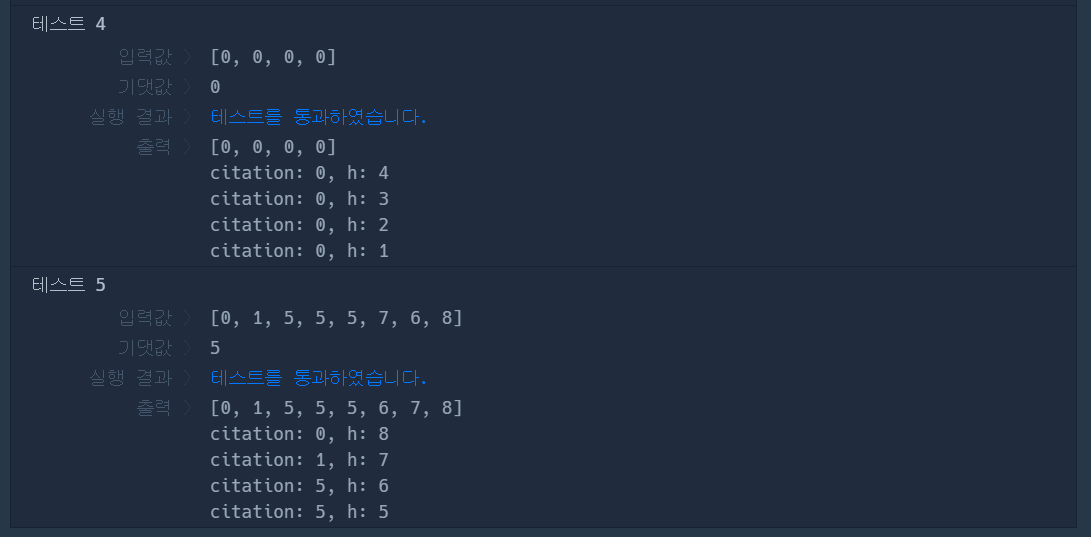
처음에는 이해가 잘 안 갔었는데 출력문을 찍어보면서 이해해보려고 노력했더니 이해할 수 있었다. 간단하게 설명하자면 n - i를 통해 H-Index가 큰 경우부터 거꾸로 검사하면서 조건에 만족할 경우 반환해서 결과를 구하는 방식이다.

아래의 테스트 케이스 1번에서 n = 5인데 n - i를 하면서 정렬된 citations를 순회하면 n - i의 값은 5, 4, 3, 2, 1이 된다. 이 값들은 현재 순회하고 있는 논문의 인용 수 이상을 인용한 논문의 수를 의미한다. 즉, 0번 인덱스의 경우는 0번 인용되었는데 0번 이상 인용된 논문의 수는 5편이고, 1번 인덱스의 경우는 1번 인용되었는데 1번 이상 인용된 논문의 수는 4편이다. 정렬을 통해서 쉽게 h번 이상 인용된 논문의 수를 구한 것이다.

우리가 구하고자 하는 조건은 h번 이상 인용된 논문의 수가 h편 이상이고, 나머지 논문이 h편 이하가 되는 h의 최댓값을 구하는 것이다.

그렇기 때문에 현재 n-i를 통해서 h가 될 수 있는 경우를 거꾸로 순회 중이니 순회하면서 위의 조건을 만족시키는 경우(h편인 논문의 최소 인용 수가 citation(h)번 이상)에 리턴을 하게 되면 그것이 정답이 되는 것이다. (만족하는 경우가 없을 경우는 마지막에 0을 리턴하면 된다.)

전체 코드 (python)

def solution(citations):
    citations.sort()
    
    n = len(citations)
    for i, citation in enumerate(citations):
        # print("citation: %d, h: %d" %(citation, n-i))
        
        # 인용된 횟수(h번 이상) >= 인용된 논문의 수(h편)
        if citation >= n - i:
            return n - i
    return 0

실행 결과

4. 핵심 정리

4.1 🔥 최종 풀이 🔥

프로그래머스에서 참고한 방식(정렬 외에 O(n))이 가장 효율성이 좋았기 때문에 최종 풀이로 결정하게 되었다. 이 외에도 프로그래머스에 좋은 풀이들이 많으니까 참고해보면 좋을 것 같다.

def solution(citations):
    citations.sort()
    
    n = len(citations)
    for i, citation in enumerate(citations):
        if citation >= n - i:
            return n - i
    return 0