Programmers | 소수 찾기 - Python

1. 개념 정리

1.1 완전 탐색 (Exhaustive Search)

컴퓨터의 빠른 계산 능력을 이용해 가능한 모든 경우의 수를 찾아서 답을 찾는 방법. '무식하게 푼다'는 의미로 Brute-Force라고 불리기도 한다.

완전 탐색의 종류

• Brute-Force (브루트 포스)
• Bitmask (비트마스크)
• Backtracking (백트래킹)
• Recursive function (재귀 함수)
• Permutation (순열)
• BFS/DFS (깊이/너비 우선 탐색)

1.2 에라토스 테네스의 체

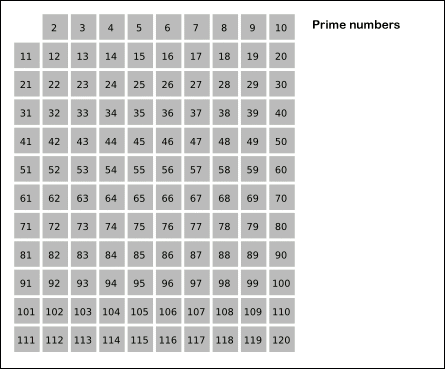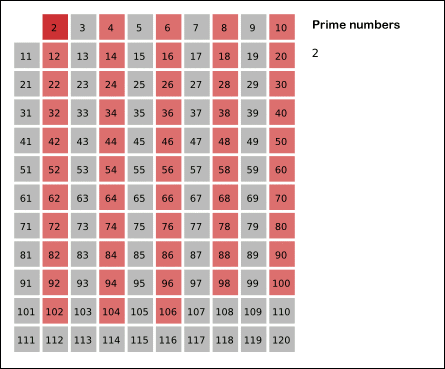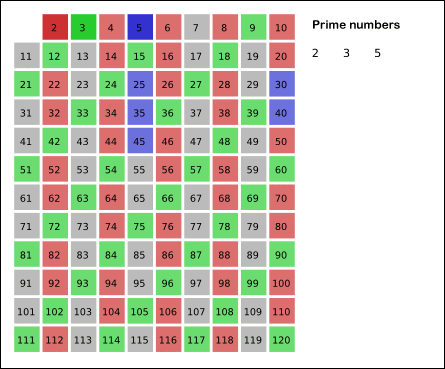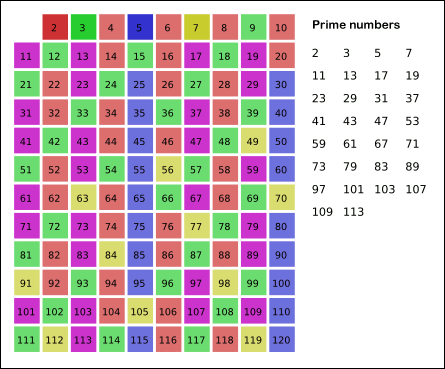
고대 그리스 수학자 에라토스테네스가 만들어 낸 소수를 찾는 방법. O(Nlog(logN))의 시간 복잡도를 가진다.

• k=2부터 √n 이하까지 반복하여 자연수들 중 k(제외되지 않았다면)를 제외한 k의 배수들을 제외시킨다.

• 위키피디아 코드

def prime_list(n):
    # 에라토스테네스의 체 초기화: n개 요소에 True 설정(소수로 간주)
    sieve = [True] * n

    # n의 최대 약수가 sqrt(n) 이하이므로 i=sqrt(n)까지 검사
    m = int(n ** 0.5)
    for i in range(2, m + 1):
        if sieve[i] == True:           # i가 소수인 경우
            for j in range(i+i, n, i): # i이후 i의 배수들을 False 판정
                sieve[j] = False

    # 소수 목록 산출
    return [i for i in range(2, n) if sieve[i] == True]

• 직접 작성한 코드

def prime_list(n):
    prime = [True] * (n + 1)
    prime[0] = prime[1] = False 
    
    for i in range(2, int(n ** 0.5) + 1):
        if prime[i]:
            for j in range(i*i, len(prime), i):
                prime[j] = False
    return prime

2. 문제 설명

2.1 소수 찾기

한자리 숫자가 적힌 종이 조각이 흩어져있습니다. 흩어진 종이 조각을 붙여 소수를 몇 개 만들 수 있는지 알아내려 합니다.

각 종이 조각에 적힌 숫자가 적힌 문자열 numbers가 주어졌을 때, 종이 조각으로 만들 수 있는 소수가 몇 개인지 return 하도록 solution 함수를 완성해주세요.

2.2 제한 조건

• numbers는 길이 1 이상 7 이하인 문자열입니다.
• numbers는 0~9까지 숫자만으로 이루어져 있습니다.
• "013"은 0, 1, 3 숫자가 적힌 종이 조각이 흩어져있다는 의미입니다.

2.3 입출력 예시

numbers	return
"17"	3
"011"	2

3. 풀이 과정

흩어진 종이 조각을 조합해서 만들 수 있는 수 중 소수의 개수를 구하는 문제이다.

제한 조건으로 주어진 numbers의 길이가 7이하이기 때문에 시간 복잡도를 크게 고려할 필요가 없어 비교적 쉽게 풀 수 있는 문제였다. 하지만, 풀이하는 과정에서 라이브러리 의존도가 높았기 때문에 라이브러리를 사용하지 않고 구현하는 것도 연습이 필요할 것 같다.

3.1 순열 + 에라토스테네스의 체 1 : 성공😋

완전 탐색 문제이기때문에 처음 접근은 종이 조각을 통해 만들 수 있는 모든 수를 구한 후 에라토스테네스의 체를 사용하여 소수를 판별하고자 했다. 풀이 과정은 다음과 같다.

1. 종이 조각으로 만들 수 있는 모든 수 구하기 => permutations 라이브러리 활용
2. 앞서 구한 수 중 중복을 제거하기 => set 활용
3. 소수 판별 => 에라토스테네스의 체

3.1.1 순열 & 중복 제거

1. permutations를 사용하여 numbers를 가지고 만들 수 있는 모든 수를 구한다.
2. 위의 결과값을 join을 활용하여 하나의 문자열로 만든다.
3. 각각의 문자열들을 int형으로 map해준다.
4. 중복을 제거하기 위해 위의 결과값을 set에 넣어준다.

• set 추가 방식으로는 update or | or union 이 있다.
• map은 리스트의 요소를 지정된 함수로 처리해주는 함수이다.

from itertools import permutations

def solution(numbers):
    numbers = list(numbers)
    number_set = set()
    
    # 가능한 모든 경우의 수 (순열) => set 사용해서 중복 제거
    for i in range(len(numbers)):
        number_set |= set(map(int, map(''.join, permutations(numbers, i+1))))

3.1.2 에라토스테네스의 체

1. 에라토스테네스의 체를 사용하여 number_set의 최댓값까지 소수 판별 리스트를 만든다.
2. number_set을 순회하면서 해당 number가 소수인 경우 answer의 값을 1 증가 시킨다.

# 에라토스테네스의 체
def prime_list(n):
    prime = [True] * (n + 1)
    prime[0] = prime[1] = False 
    
    for i in range(2, int(n ** 0.5) + 1):
        if prime[i]:
            for j in range(i*i, len(prime), i):
                prime[j] = False
    return prime

# 에라토스테네스의 체로 소수 판별 리스트 생성
prime = prime_list(max(number_set))

# 소수 판별
answer = 0
for number in number_set:
    if prime[number]:
        answer += 1
return answer

3.1.3 전체 코드

• 전체 코드 (python)

from itertools import permutations

# 에라토스테네스의 체
def prime_list(n):
    prime = [True] * (n + 1)
    prime[0] = prime[1] = False 
    
    for i in range(2, int(n ** 0.5) + 1):
        if prime[i]:
            for j in range(i*i, len(prime), i):
                prime[j] = False
    return prime
    
def solution(numbers):
    numbers = list(numbers)
    number_set = set()
    
    # 가능한 모든 경우의 수 (순열) => set 사용해서 중복 제거
    for i in range(len(numbers)):
        number_set |= set(map(int, map(''.join, permutations(numbers, i+1))))
    
    # 에라토스테네스의 체로 소수 판별 리스트 생성
    prime = prime_list(max(number_set))
    
    # 소수 판별
    answer = 0
    for number in number_set:
        if prime[number]:
            answer += 1
    return answer

• 실행 결과
  

3.2 순열 + 에라토스테네스의 체 2 : 성공😋

앞의 방식과 기본적인 부분은 동일하지만 에라토스테네스의 체를 이용할 때 별도의 리스트를 생성하지 않고, set을 활용하여 소수가 아닌 수를 제거하는 방식이다.

시간이나 메모리 측면에서 더 효율적이지 않을까 기대했는데, 실제로 실행 결과를 보니 위의 방식보다 오히려 효율이 안 좋아졌다. 아마 반복문에서set을 사용한 것 때문에 그런 것 같다고 추측만 해보았다..(실제로 그런지는 잘 모르겠다..)

3.2.1 소수 아닌 수 제거

1. number_set에서 0~1까지 제거한다.
2. 2부터 √n까지 반복하며 소수가 아닌 수들을 제거한다.
3. number_set의 길이를 반환한다.

n =  max(number_set)
# 0~1 제거
number_set -= set(range(0, 2)) 
for i in range(2, int(n ** 0.5) + 1):
    # 소수 아닌 수 제거
    number_set -= set(range(i*i, n+1, i))

return len(number_set)

3.2.2 전체 코드

• 전체 코드 (python)

from itertools import permutations

def solution(numbers):
    numbers = list(numbers)
    number_set = set()
    
    # 가능한 모든 경우의 수 (순열) => set 사용해서 중복 제거
    for i in range(len(numbers)):
        number_set |= set(map(int, map(''.join, permutations(numbers, i+1))))
    
    n =  max(number_set)
    # 0~1 제거
    number_set -= set(range(0, 2)) 
    for i in range(2, int(n ** 0.5) + 1):
        # 소수 아닌 수 제거
        number_set -= set(range(i*i, n+1, i))
        
    return len(number_set)

• 실행 결과
  

4. 핵심 정리

4.1 🔥 최종 풀이 🔥

from itertools import permutations

def prime_list(n):
    prime = [True] * (n + 1)
    prime[0] = prime[1] = False 
    
    for i in range(2, int(n ** 0.5) + 1):
        if prime[i]:
            for j in range(i*i, len(prime), i):
                prime[j] = False
    return prime
    
def solution(numbers):
    numbers = list(numbers)
    number_set = set()
    
    for i in range(len(numbers)):
        number_set |= set(map(int, map(''.join, permutations(numbers, i+1))))
    
    prime = prime_list(max(number_set))
    
    answer = 0
    for number in number_set:
        if prime[number]:
            answer += 1
    return answer

4.2 핵심 포인트

• 순열 permutations
• 에라토스테네스의 체
• set과 map
• 시간이 된다면 라이브러리 사용하지않고 순열 구현해보기!!

4.3 주요 라이브러리

• permutations

4.4 참고 링크

• JAVA [자바] - 소수 구하는 알고리즘 및 구현
• [Algorithm] 에라토스테네스의 체
• Python 내장 함수 : set 함수 사용하기 - 아이공