Programmers | 주식가격 - Python

1. 개념 정리

1.1 스택 (Stack)

후입 선출 구조 Last In First Out(LIFO)로 나중에 들어간 것이 먼저 나오는 구조이다.

파이썬에서는 별도의 라이브러리 사용 없이 기본 리스트를 사용하여 스택을 구현할 수 있다.

stack = []

stack.append(1) # 삽입 O(1)
stack.pop() # 삭제 O(1)

stack[-1] # 삭제 하지 않고 최상단 원소 가져오기
print(stack) # 최하단 원소부터 출력
print(stack[::-1]) #최상단 원소부터 출력

1.2 큐 (Queue)

선입 선출 구조 First In First Out(FIFO)로 먼저 들어간 것이 먼저 나오는 구조이다.

별도의 라이브러리 없이 리스트를 사용하여 pop(0) or insert(0, x) 통해서도 구현할 수 있지만 시간복잡도가 O(n)이기 때문에 불리한 연산이다. 그렇기 때문에 별도의 라이브러리를 사용해서 구현하는 것이 좋다.

파이썬에서는 collections에서 제공하는 deque를 활용하는 것이 좋다. deque는 스택과 큐의 장점을 모두 채택한 것으로 데이터를 양방향에서 추가하고 제거할 수 있는 자료구조로, 데이터를 넣고 빼는 속도가 리스트 자료형에 비해서 효율적이다.

자세한 설명은 하단의 참고 링크에 있으니 한 번 읽어보면 좋을 것 같다!

from collections import deque

queue = deque() # 리스트를 변수로 사용 가능

queue.append(1) # 삽입 O(1)
queue.popleft() # 삭제 O(1)

print(queue) # 먼저 들어온 순서대로 출력
queue.reverse() # 다음 출력을 위해 역순으로 바꾸기
print(queue) # 나중에 들어온 원소부터 출력

2. 문제 설명

2.1 주식가격

초 단위로 기록된 주식가격이 담긴 배열 prices가 매개변수로 주어질 때, 가격이 떨어지지 않은 기간은 몇 초인지를 return 하도록 solution 함수를 완성하세요.

2.2 제한 조건

• prices의 각 가격은 1 이상 10,000 이하인 자연수입니다.
• prices의 길이는 2 이상 100,000 이하입니다.

2.3 입출력 예시

prices	return
[1, 2, 3, 2, 3]	[4, 3, 1, 1, 0]

3. 풀이 과정

주식 가격이 떨어지지 않은 기간을 구하는 비교적 간단한 문제이다. 처음 풀이했을 때 쉽게 정답을 맞출 수 있어서 level2 난이도까지는 아니라고 생각했는데, 효율성 검사도 추가되어서 효율성 측면도 고려한다면 다양한 방식으로 풀이가 가능하기 때문에 다시 한번 생각해보게 된 문제이다.

3.1 Queue(FIFO) 활용: 성공😋

간단하게 반복문을 2 중첩해서 풀 수 있었다. 인덱스가 0인 시점부터 가격이 떨어질 때까지의 초를 세고, 인덱스가 1인 시점부터 가격이 떨어질 때까지의 초를 세고, 이 과정을 모든 인덱스에 반복하는 것이다.

큐를 사용한다면 추가적인 인덱싱 없이 더 간편하게 구현이 가능할 것 같아서 큐도 활용하였다. prices로 queue를 초기화 시킨 후에 반복문을 돌면서 앞에서부터 하나씩 popleft해서 popleft한 뒤의, 남은 queue를 순회하며 값이 작아지기 전까지 초를 증가시키는 것을 queue가 빌때까지 반복하면 된다. 구현 코드는 다음과 같다.

• 전체 코드 (python)

from collections import deque

def solution(prices):
    queue = deque(prices)
    answer = []
    
    while queue:
        price = queue.popleft()
        sec = 0
        for q in queue:
            sec += 1
            if price > q:
                break 
        answer.append(sec)        
    return answer

• 실행 결과
  

3.2 Stack(LIFO) 활용 : 성공😋

위의 풀이로 풀었을 때 시간 효율이 괜찮다고 생각되어 추가적인 풀이를 고려하지 않았었는데, 스터디를 진행하며 위의 효율에서 2배는 좋아진 알고리즘을 알게되어 추가한다. 프로그래머스에서도 보기 힘든 풀이 방식이니까 한 번 눈여겨 보면 좋을 것 같다.

스택을 활용하여 값이 작아졌을 경우에만 스택에 남아있는 이전의 값들을 비교하는 방식이다. 알고리즘은 다음과 같다.

1. answer의 값을 주식의 가격이 떨어지지 않았을 경우로 초기화한다.
2. prices를 순회하며 stack의 top의 인덱스보다 현재 price의 값이 작을 경우,
   1. pop후, answer값을 수정하는 것을 반복한다.

3.2.1 answer을 max값으로 초기화

1. 모든 prices의 값이 떨어지지 않았다는 가정하에 answer의 값을 초기화한다.

• prices = [1, 2, 3, 2, 3, 1]일 경우 answer = [5, 4, 3, 2, 1, 0]

# answer을 max값으로 초기화  
    answer = [ i for i in range (length - 1, -1, -1)]

3.2.2 주식 가격이 떨어질 경우 찾기

prices를 순회할 때 증가하는 경우에는 answer의 값을 변경할 필요가 없다. 하지만, 감소하는 경우가 있다면 그 때 이전의 stack에 저장된 인덱스들을 비교 후 감소하는 경우라면 해당 answer의 값을 (작아질 때의 인덱스 - stack의 인덱스) 를 구해서 감소하기 전의 시간을 구해 answer의 값을 업데이트 하는 방식이다. 알고리즘은 다음과 같다. (이해가 잘 안된다면 아래의 출력 예시를 따라하며 이해해보자!)

1. stack의 초기값에는 0번 인덱스를 넣어준다.
2. prices를 순회한다. (1~n-1까지)
   1. stack이 있을 경우, 현재 순회하는 값이 stack의 top 인덱스에 해당하는 prices의 값보다 작을 경우 아래 과정을 반복한다.
      1. stack에서 값을 pop한다.
      2. 위에서 pop한 인덱스의 answer 값을 (작아질 때의 인덱스 - pop한 인덱스)로 변경한다.
   2. stack에 순회하는 인덱스를 append한다.

stack = [0]
    for i in range (1, length):
        # print(i, stack)
        while stack and prices[stack[-1]] > prices[i]:
            j = stack.pop()
            answer[j] = i - j
            # print(i, j, stack)
        stack.append(i)

• Stack 출력예시
  

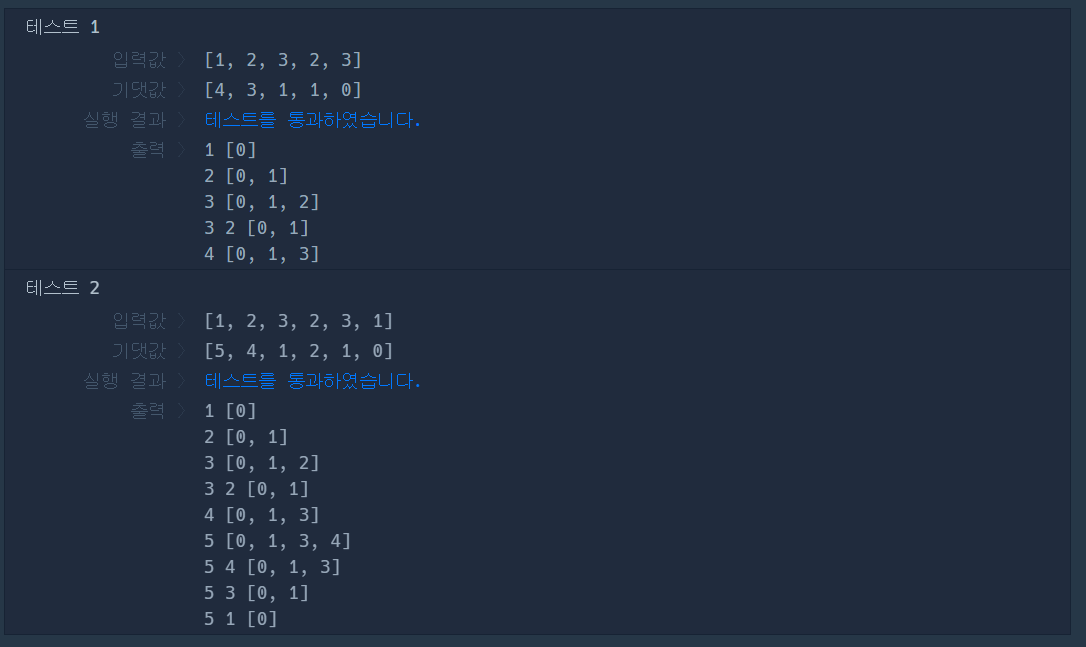
3.2.3 전체 코드

• 전체 코드 (python)

# prices = [1, 2, 3, 2, 3, 1] return [5, 4, 1, 2, 1, 0]
def solution(prices):
    length = len(prices)
    
    # answer을 max값으로 초기화  
    answer = [ i for i in range (length - 1, -1, -1)]
    
    # 주식 가격이 떨어질 경우 찾기
    stack = [0]
    for i in range (1, length):
        while stack and prices[stack[-1]] > prices[i]:
            j = stack.pop()
            answer[j] = i - j
        stack.append(i)
    return answer

• 실행 결과
  

4. 핵심 정리

4.1 🔥 최종 풀이 🔥

def solution(prices):
    length = len(prices)
    answer = [ i for i in range (length - 1, -1, -1)]
    
    stack = [0]
    for i in range (1, length, 1):
        while stack and prices[stack[-1]] > prices[i]:
            j = stack.pop()
            answer[j] = i - j
        stack.append(i)
    return answer

4.2 핵심 포인트

• stack과 deque
• 효율성을 고려한 풀이 방식

4.3 주요 라이브러리

• list

• deque

4.4 참고 링크

• 스택 (STACK), 큐(QUEUE) 개념/비교 /활용 예시

• 파이썬에서 큐(queue) 자료 구조 사용하기