" 데이터 분석에서 통계가 중요한 이유 ! "
통계는 의사결정을 뒷받침하는 핵심 도구
데이터 속 의미를 검증하고, 신뢰할 수 있는 결론 도출을 도움
즉, 기업이 보다 현명한 결정을 내려 수익을 창출할 수 있도록 도움
" 기술통계 vs 추론통계 "
기술통계
데이터를 요약하고 설명하는 통계 방법
평균, 중앙값, 분산, 표준편차 등 데이터를 특정 대푯값으로 요약
장점 : 데이터의 전반적 특징을 간단하고 빠르게 파악 가능
단점 : 이상치에 민감, 데이터의 세부적인 특성까지 설명하기는 어려움
ex) 회사의 매출 데이터를 요약하기 위해 평균 매출, 매출의 표준편차 등을 계산
추론통계
데이터의 일부로 전체를 추정하는 통계 방법
신뢰구간, 가설검정 등을 사용하여 표본을 통해 모집단의 특성을 추정하고 가설을 검정
장점 : 모집단 전체를 직접 조사하지 않고도 특성 추정 가능
단점 : 표본 추출 방식에 따라 결과 왜곡 가능, 확률적 불확실성과 오차가 항상 존재
ex) 일부 고객의 설문조사를 통해 전체 고객의 만족도를 추정
" 다양한 분석 방법들 개요 "
위치 추정
데이터의 중심을 확인하는 방법
[ 평균, 중앙값 ]
ex) 학생들의 시험 점수에서 평균 점수, 중간 점수를 계산
data = [85, 90, 78, 92, 88, 76, 95, 89, 84, 91]
mean = np.mean(data) # 평균
median = np.median(data) # 중앙값
print(f'평균: {mean}, 중앙값 : {median}')변이 추정
데이터들이 서로 얼마나 다른지 확인하는 방법
[ 분산, 표준편차, 범위 ]
ex) 매출 데이터의 변이를 분석하여 비즈니스 안정성을 평가
data = [85, 90, 78, 92, 88, 76, 95, 89, 84, 91]
veriance = np.var(data) # 분산
std_dev = np.std(data) # 표준편차
data_range = np.max(data) - np.min(data) # 범위
print(f'분산: {veriance}, 표준편차 : {std_dev}, 범위: {data_range}')분포 탐색
데이터들이 어떻게 구성되어 있는지 확인하는 방법
[ 히스토그램, 상자 그림 ]
ex) 시험 점수의 분포를 히스토그램과 상자 그림으로 표현
data = [85, 90, 78, 92, 88, 76, 95, 89, 84, 91]
# 히스토그램
plt.hist(data, bins=5)
plt.title('histogram')
plt.show()
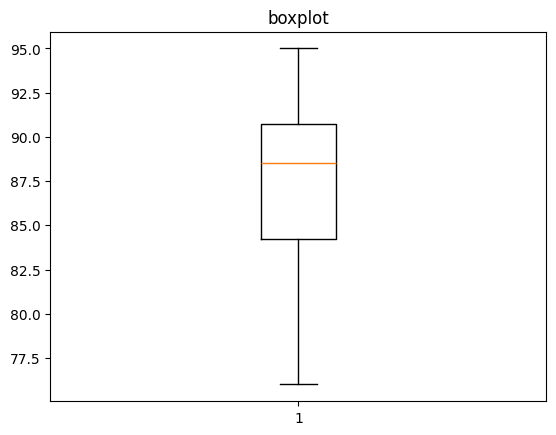
# 박스플롯
plt.boxplot(data)
plt.title('boxplot')
plt.show()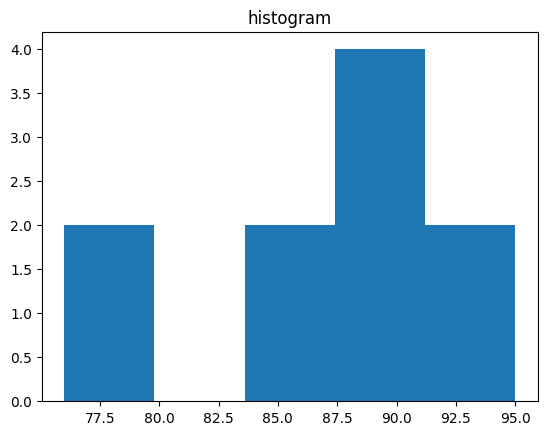 |
 |
이진 & 범주 데이터 탐색
서로 얼마나 다른지 확인하는 방법
[ 최빈값, 파이 차트, 막대 그래프 ]
ex) 고객 만족도 설문에서 만족 / 불만족의 빈도 분석
satisfaction = ['satisfaction', 'satisfaction', 'dissatisfaction',
'satisfaction', 'dissatisfaction', 'satisfaction', 'satisfaction',
'dissatisfaction', 'satisfaction', 'dissatisfaction']
satisfaction_counts = pd.Series(satisfaction).value_counts()
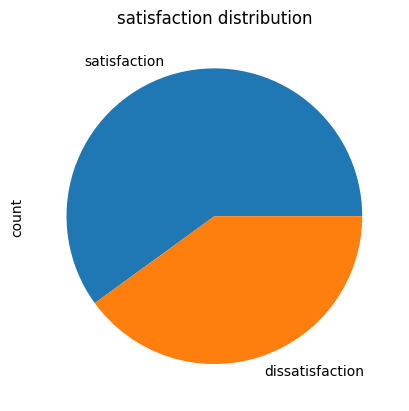
# 파이 차트
satisfaction_counts.plot(kind='pie')
plt.title('satisfaction distribution')
plt.show()
# 막대 그래프
satisfaction_counts.plot(kind='bar')
plt.title('satisfaction distribution')
plt.show()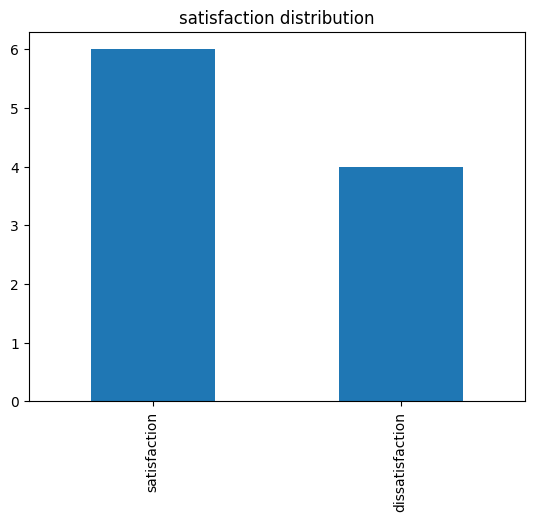 |
 |
상관관계
서로 관련이 있는지 확인하는 방법
[ 상관계수, 산점도 ]
- 상관계수 : 두 변수 간의 관계를 측정하는 방법
- 상관계수 = -1 or 1 : 강력한 (음 / 양)의 상관관계
- 상관계수 = 0 : 상관관계 없음, ≠ 독립
" 상관관계 ≠ 인과관계 "
- 상관관계 : 두 변수 간의 연관성을 나타냄
- 인과관계 : 한 변수가 다른 변수에 미치는 영향을 나타냄
ex) 고객 만족도 설문에서 만족 / 불만족의 빈도 분석
study_hours = [10, 9, 8, 7, 6, 5, 4, 3, 2, 1]
exam_scores = [95, 90, 85, 80, 75, 70, 65, 60, 55, 50]
correlation = np.corrcoef(study_hours, exam_scores)[0, 1]
print(f"공부 시간과 시험 점수 간의 상관계수: {correlation}")
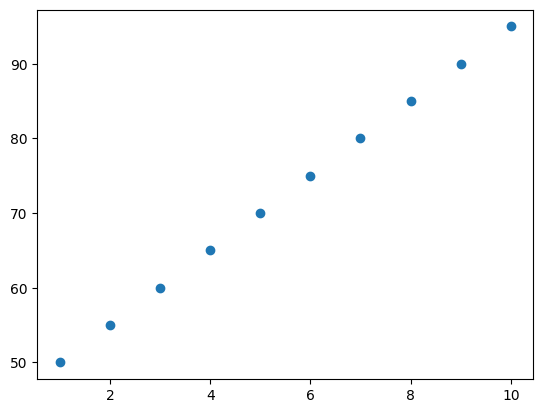
plt.scatter(study_hours, exam_scores)
plt.show()공부 시간과 시험 점수 간의 상관계수: 1.0
다변량 분석
여러 데이터들 간 관계를 확인하는 방법
[ 산점도 + 히스토그램/커널밀도(KDE), 히트맵 ]
ex) 여러 마케팅 채널의 광고비와 매출 간의 관계 분석
data = {'TV': [230.1, 44.5, 17.2, 151.5, 180.8],
'Radio': [37.8, 39.3, 45.9, 41.3, 10.8],
'Newspaper': [69.2, 45.1, 69.3, 58.5, 58.4],
'Sales': [22.1, 10.4, 9.3, 18.5, 12.9]}
df = pd.DataFrame(data)
# 산점도 + 히스토그램
sns.pairplot(df)
plt.show()
# 히트맵
sns.heatmap(df.corr())
plt.show()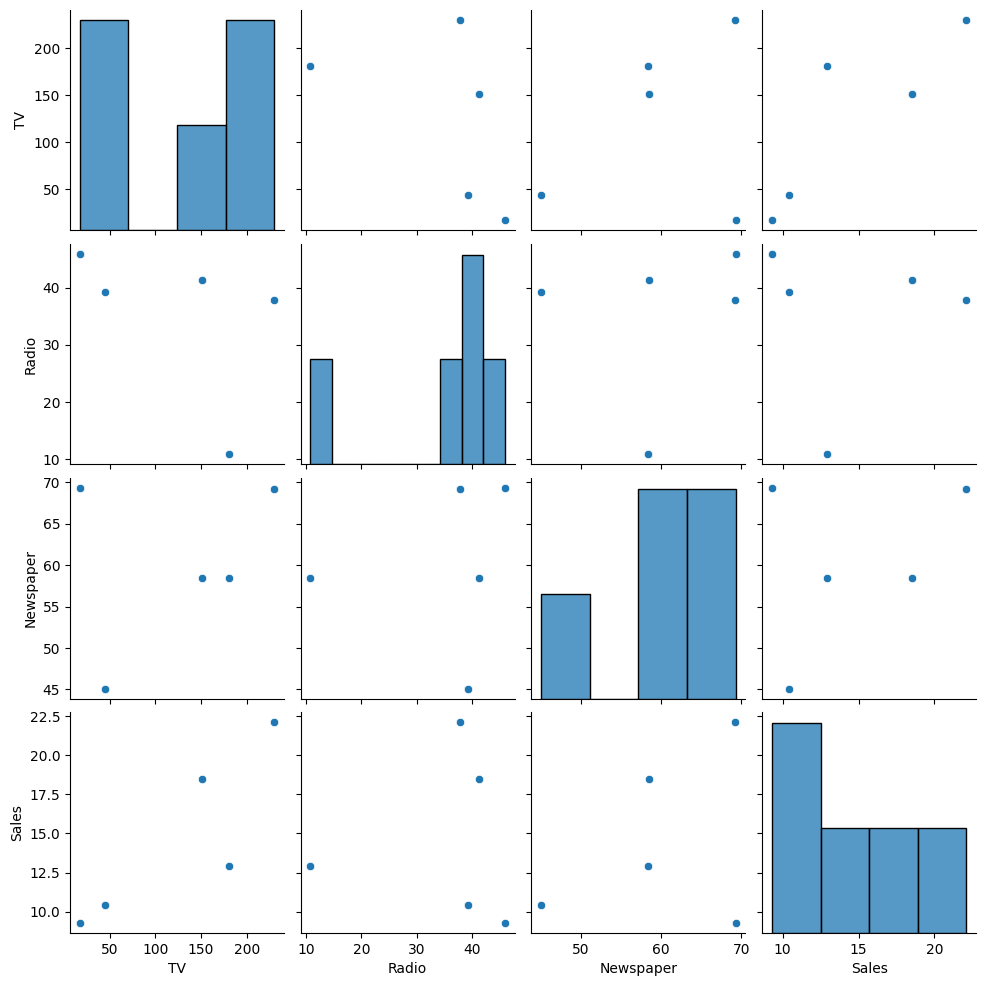 |
 |
" 개념 정리 "
평균(Mean)
데이터의 대푯값을 나타내는 값
계산 : 모든 데이터를 더한 후 데이터의 개수로 나눔
특징 : 데이터의 일반적인 경향 파악에 유용
중앙값(Median)
데이터셋을 오름차순 정렬했을 때 중앙에 위치한 값
특징 : 이상치에 덜 민감함
분산(Variance)
평균으로부터 얼마나 떨어져 있는지 나타내는 척도, 데이터의 변동성 측정
계산 : (각 데이터 값 - 평균)**2을 모두 더한 뒤 데이터의 개수로 나눔
특징 : 분산이 크면 데이터가 넓게 퍼져 있고 작으면 데이터가 평균에 가깝게 모여 있음을 의미
표준편차(Standard Deviation)
평균으로부터 얼마나 떨어져 있는지 나타내는 척도, 데이터의 변동성 측정
계산 : 분산의 양의 제곱근
특징 : 표준편차가 크면 데이터가 넓게 퍼져 있고 작으면 데이터가 평균에 가깝게 모여 있음을 의미
" 분산과 표준편차의 관계 "
데이터의 변동성을 측정하는 척도
분산 : 제곱 단위로 표현
표준편차 : 원래 데이터 값과 동일한 단위로 표현
신뢰구간(Confidence Interval)
모집단의 평균이 특정 범위 내에 있을 것이라는 확률
일반적으로 95%, 모집단 평균이 95% 확률로 해당 구간 내에 있음을 의미
가설검정(Hypothesis Testing)
모집단에 대한 가설을 검증하기 위해 사용
귀무가설(H0) : 검증하고자 하는 가설이 틀렸음을 나타내는 기본 가설(변화가 없다, 효과가 없다 등)
대립가설(H1) : 그 반대 가설로 주장하는 바를 나타냄(변화가 있다, 효과가 있다 등)



퍼가요~♡