강의에서 다룰 것들
- Definitions
- liner regression
- Batch Gradient Descent
- Stochastic Gradient Descent (SGD)
- Normal equations
Supervised Learning
Prediction function
예측하는 함수.
x는 우리가 넣는 데이터, y는 우리가 예측할 카테고리 종류 즉 타겟이다
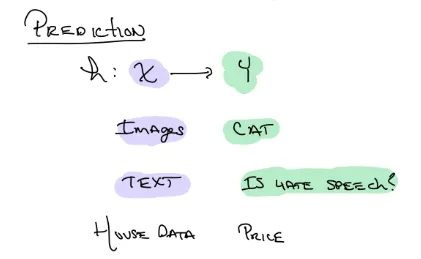
목적: 좋은 h 함수를 찾는 것. 이 함수는 거대하기 때문에 실제 실험할때는 여러 제한이 필요하다
머신러닝은 Interpolation(보간, 직선에 한 점 비어있으면 그 점을 구하는 느낌)을 하는게 아니다. 즉 주어진 값들을 분석해서 빈곳을 메꾸는것이 아니라 이전 데이터들을 바탕으로 새롭게 들어온 데이터의 결과 값을 예측하는 것이다. 그렇기 때문에 머신러닝은 사실 상 prediction 을 하는것이다.
“We care about new values not in training dataset”
함수종류
y 가 이산적이면 → classification(분류) ex. 일치여부(binary classfication), 종류예측
y 가 연속적이면 → regression(연속) ex. house data

함수 수식
-
linear regression
-
feature 1개

-
feature 여러개
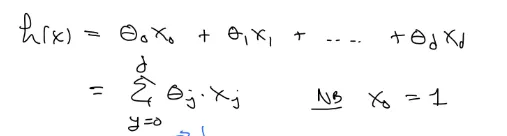
편의상 x0 은 1로 둬서 식을 깔끔하게 표현하기로 하자.
-
Vector notation
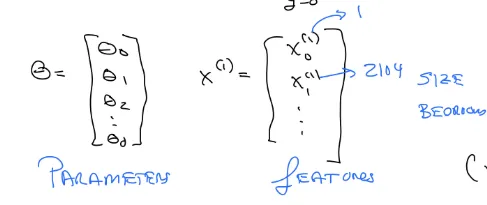
θ는 parameters, 변수앞에 붙는 계수 같은거다.
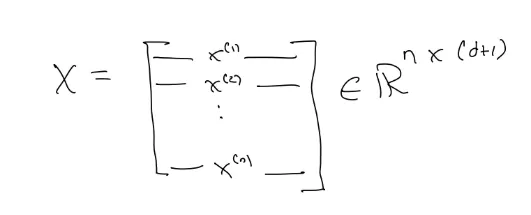
X matrix 에서 각각의 데이터 예시가 한 row가 되고, feature들이 column 이 된다
행렬의 차원이 n *(d+1)인 이유는
⇒ n 개의 데이터가 있고, d 개의 feature 이 있으면 X0 포함해서 d+1 이기 때문이다
Gradient Descent
좋은 예측, 즉 좋은 함수를 만들기 위해서는 에러 값을 줄여야 한다.
그렇기 위해서 θ값이 언제일때 J(θ) 가 가장 작아지는지 확인해야함
Cost function(least squares)
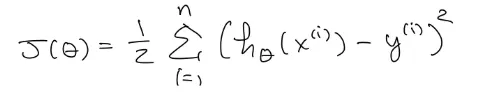
1/2 은 최솟값을 찾는데 영향을 주지 않고 미분할때 1/2 이 편하기 때문에 붙임. 실질적으로 계산 복잡도가 높아지지는 않음.

초기 θ 값(랜덤 또는 0)에서의 미분계수 값을 구하고 음수면 오른쪽으로, 양수면 왼쪽으로 θ값을 업데이트 시킨다. 여기서 α, learning rate 는 한번 업데이트 시킬때 얼마나 큰 폭으로 수정하는지를 뜻함. 실제로는 α가 t( 업데이트 횟수, step) 와 관련이 있지만, t를 바꿀때마다 α값을 다르게 업데이트 하는게 유리하므로, 이 수식에서는 독립적인 변수이다. 이런 점에 대한 연구들이 진행되고 있다.
θ 를 업데이트 하다가 변경이 거의 되지 않을때, 즉 그래프상 극소에서 멈추게 된다. 그러나 높은 차원에서는 최솟값이 아닌 극솟값에서 최솟값이라고 판단하여 멈추게 되는 문제가 발생한다.
어찌되었던, J(θ)의 최솟값을 알기 위해 이를 θ에 관해 미분을 해보자.
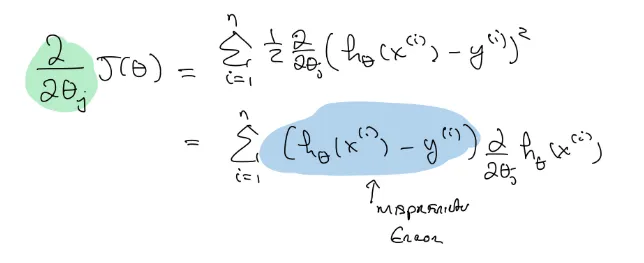
합성함수 미분에 의해 이렇게 나오고,

각각의 θ0, θ1, θ2, θ3…는 다른 변수이니 일반화 시켜서 θj 에 관한 미분을 하면 xj 가 나온다.
즉 error * xj 의 합이 도함수가 되는것
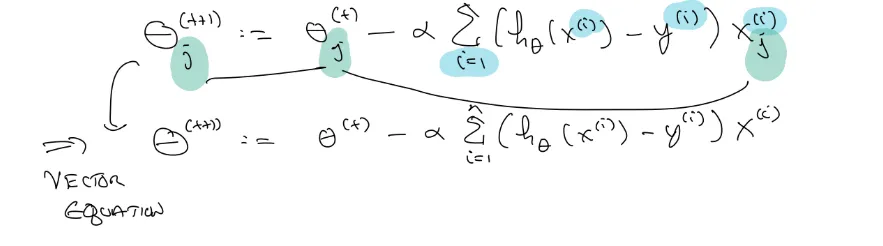
맨 처음 θt 함수에 대입해보고 일반화 시키면 다음과 같은 식이 된다.
Batch vs Stochastic Gradient Descent (SGD)
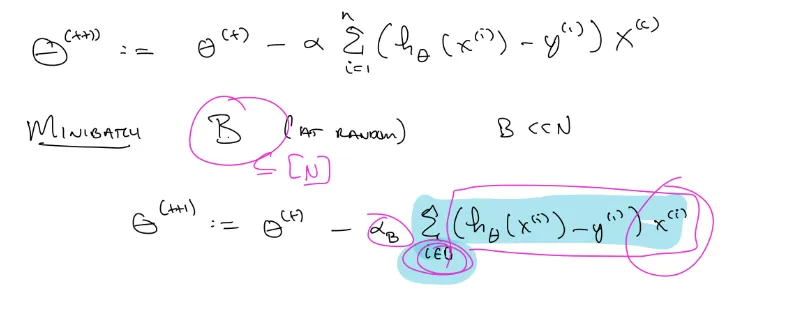
실제 모델을 학습 시킬때 시그마의 n, d 가 엄청 크다. 자원(시간, 돈)이 한정적이기 때문에 더 효과적인 학습방법을 찾아야함.
minibatch 는 순서를 셔플해서 n 보다 작은 b 개 만큼의 batch를 정해서 미분하고 그만큼 더 업데이트 하는것이다!