Binary Search Tree

Binary Search Tree

이진트리(binary tree)는 자식 노드가 최대 두 개인 노드들로 구성된 트리. 두 개의 자식 노드는 왼쪽 자식 노드와 오른쪽 자식 노드로 나눌 수 있음.
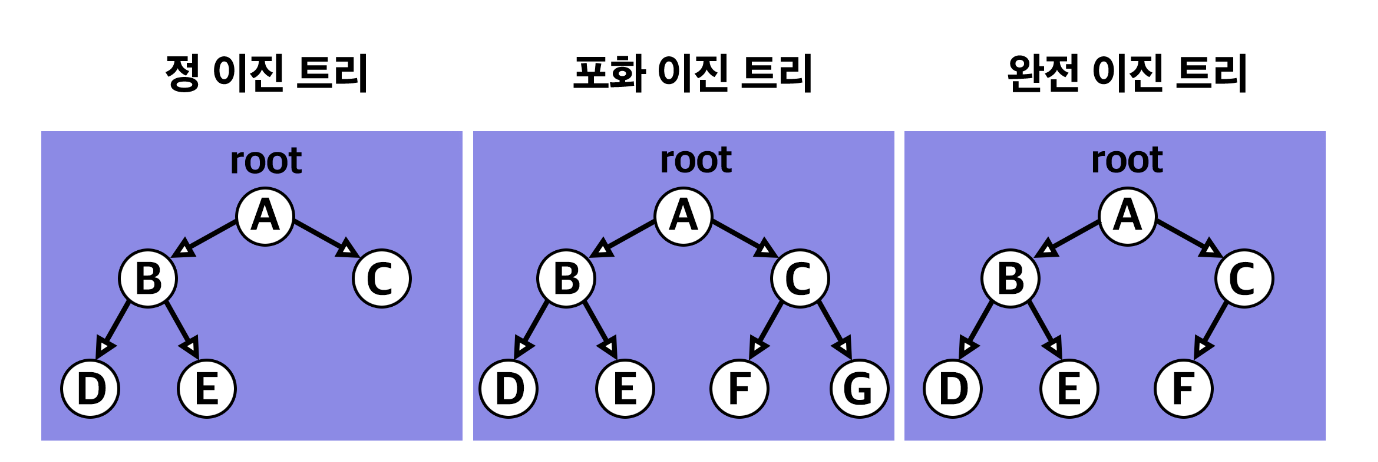
이진 트리는 자료의 삽입, 삭제 방법에 따라 정 이진 트리(full bianry tree), 완전 이진 트리(complete binary tree), 포화 이진 트리(perfect binary tree)로 나뉘어짐.

이진 트리 종류	영어 표기	설명
정 이진 트리	Full binary tree	각 노드가 0개 혹은 2개의 자식 노드를 가짐
포화 이진 트리	Perfect binary tree	정 이진 트리면서 완전 이진트리인 경우. 모든 리프 노드의 레벨이 동일하고, 모든 레벨이 가득 채워져 잇는 트리
완전 이진 트리	Complete binary tree	마지막 레벨을 제외한 모든 노드가 가득 차 있어야 하고, 마지막 레벨의 노드는 전부 차 있지 않아도 되지만 왼쪽이 채워져 있어야 함

이진 탐색 트리는 모든 왼쪽 자식의 값이 루트나 부모보다 작고, 모든 오른쪽 자식의 값이 루트나 부모보다 큰 값을 가지는 특징이 있음.

이진 탐색 트리는 균형 잡힌 트리가 아닐 때, 입력되는 값의 순서에 따라 한쪽으로 노드들이 몰리게 될 수 있음. 균형이 잡히지 않은 트리는 탐색하는 데 시간이 더 걸리는 경우가 있기 때문에 해결해야할 문제임. 이 문제를 해결하기 위해 삽입과 삭제마다 트리의 구조를 재조정하는 과정을 거치는 알고리즘을 추가할 수 있음.

연습 문제 - 이진 탐색 트리

import java.util.*;

public class Solution { 
	private int[][] graph;

  public void setGraph(int size) {
    graph = new int[size][size];

    for(int i = 0; i < size; i++) {
      for(int j = 0; j < size; j++) {
        graph[i][j] = 0;
      }
    }
  }
  public int[][] getGraph() {
    return graph;
  }
  public void addEdge(int from, int to) {
    if(from >= graph.length || to >= graph.length) return;
    graph[from][to] = 1;
  }

  public boolean hasEdge(int from, int to) {
    if(from >= graph.length || to >= graph.length) return false;
    else if(graph[from][to] == 1) return true;
    else return false;
  }

  public void removeEdge(int from, int to) {
    if(from >= graph.length || to >= graph.length) return;
    graph[from][to] = 0;
  }
}

연습 문제 - 인접 행렬 생성하기

문제

방향이 있는 간선과 방향이 없는 간선들의 목록들을 받아 2차원 배열의 인접행렬을 반환하는 함수를 작성하세요.

조건

각 간선은 3가지 정보를 담고 있습니다.

• 0번째: 간선의 시작 정점 (0 이상의 정수)
• 1번째: 간선의 도착 정점 (0 이상의 정수)
• 2번째: 방향성 (1 == 일시 무향, 0 == 일시 방향)

import java.util.*;

public class Solution { 
	public int[][] createMatrix(int[][] edges) {
    int[][] graph;

    // 행렬의 크기를 구합니다.
	  // edgesLength 변수를 0으로 할당하고, edges를 전부 순회해 제일 큰 숫자를 max에 할당합니다.
	  // edgesLength 크지 않을 경우엔 바꾸지 않습니다.
    int edgesLength = 0;

    for (int i = 0; i < edges.length; i++) {
      for (int j = 0; j < edges[i].length; j++) {
        if (edgesLength < edges[i][j]) edgesLength = edges[i][j];
      }
    }
    // matrix의 뼈대를 잡습니다.
    // max로 구한 최대값에 1을 더하여 array를 생성합니다.(0번째부터 있기 때문입니다)
    // 자동으로 모든 배열의 요소는 0으로 만들어집니다.
    graph = new int[edgesLength + 1][edgesLength + 1];

    // edges를 순회하며 무향인 곳엔 각각의 간선에 1로 바꾸어 주고, 방향이 있는 간선엔 해당 간선에만 1로 바꾸어 줍니다.
	  // 만약, [0, 3, 0]가 들어왔다면,
	  // 만들어 둔 result의 0 번째 row에 3 번째 col에 1을 추가합니다.
	  // [ 0, 0, 0, 1 ] => 0번째 버텍스가 갈 수 있는 간선 중, 3 번으로 가는 간선만 갈 수 있습니다.
    for(int i = 0; i < edges.length; i++) {
      int from = edges[i][0];
      int to = edges[i][1];
      int direction = edges[i][2];
      //일시 방향일 경우
      if(direction == 0) graph[from][to] = 1;
      //일시 무향일 경우
      else if(direction == 1) {
        graph[from][to] = 1;
        graph[to][from] = 1;
      }
    }
    return graph;
  }
}