그래프(Graph)

Graph

Graph의 정의

• 그래프: 여러 개의 점들이 서로 복잡하게 연결되어 있는 관계를 표현한 자료 구조
• 자료 구조의 그래프: 거미줄처럼 여러개의 점들이 선으로 이어져 있는 복잡한 네트워크망과 같은 모습을 띔
  

Graph의 구조

• 직접적인 관계가 있는 경우 두 점 사이를 이어주는 선이 있음
• 간접적인 관계라면 몇 개의 점과 선에 걸쳐 이어짐
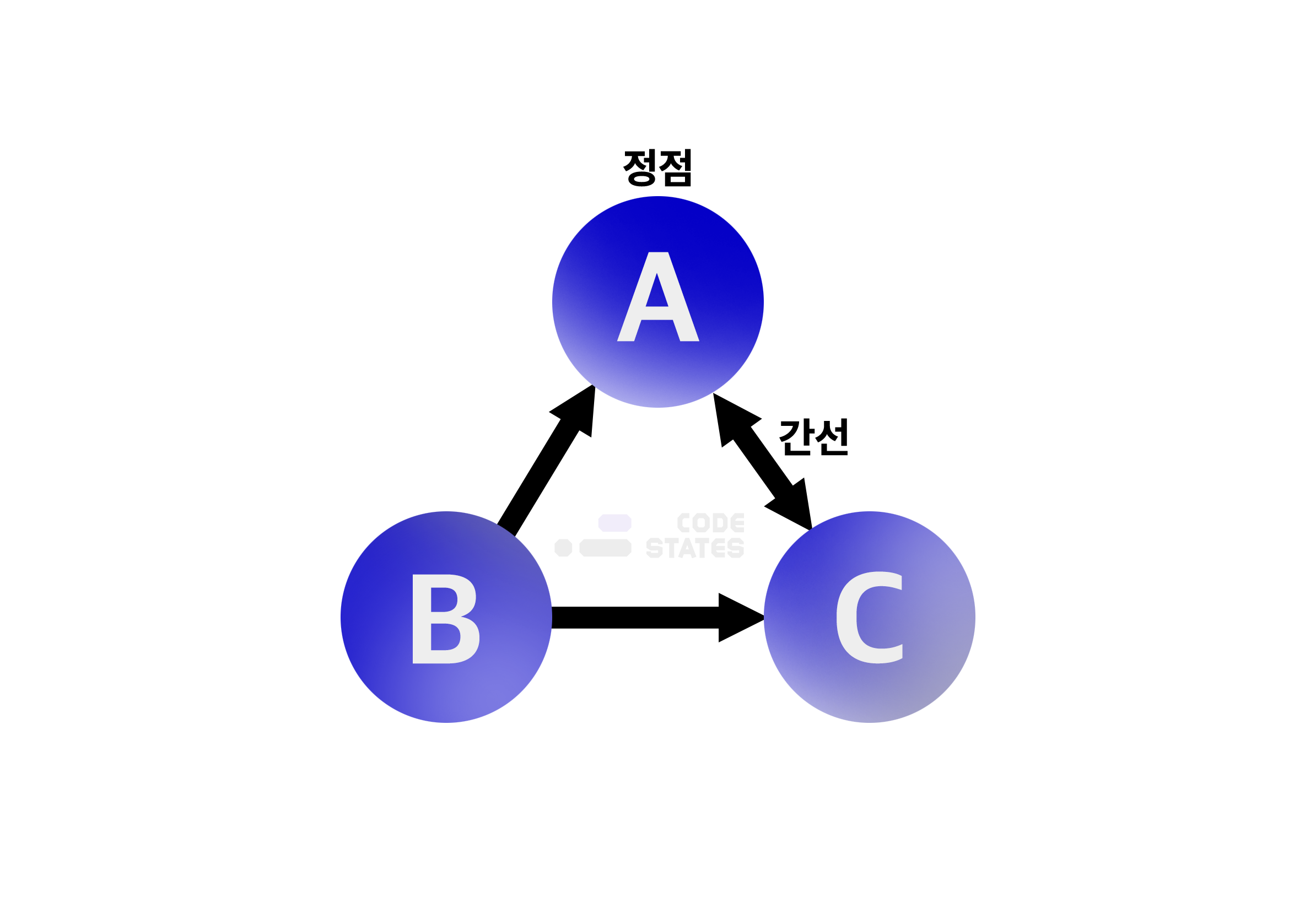
• 하나의 점을 그래프에서는 정점(vertex)이라고 표현하고, 하나의 선은 간선(edge)이라고 함.
  

Graph의 표현 방식

인접행렬
- 두 정점을 바로 이어주는 간선이 있다면 이 두 정점은 인접한다고 이야기함.
- 인접 행렬은 서로 다른 정점들이 인접한 상태인지를 표시한 행렬로 2차원 배열의 형태로 나타냄.
- 만약 A라는 정점과 B라는 정점이 이어져 있다면 1(true), 이어져 있지 않다면 0(false)으로 표시한 일종의 표임.
- 만약 가중치 그래프라면 1 대신 관계에서 의미 있는 값을 저장함.

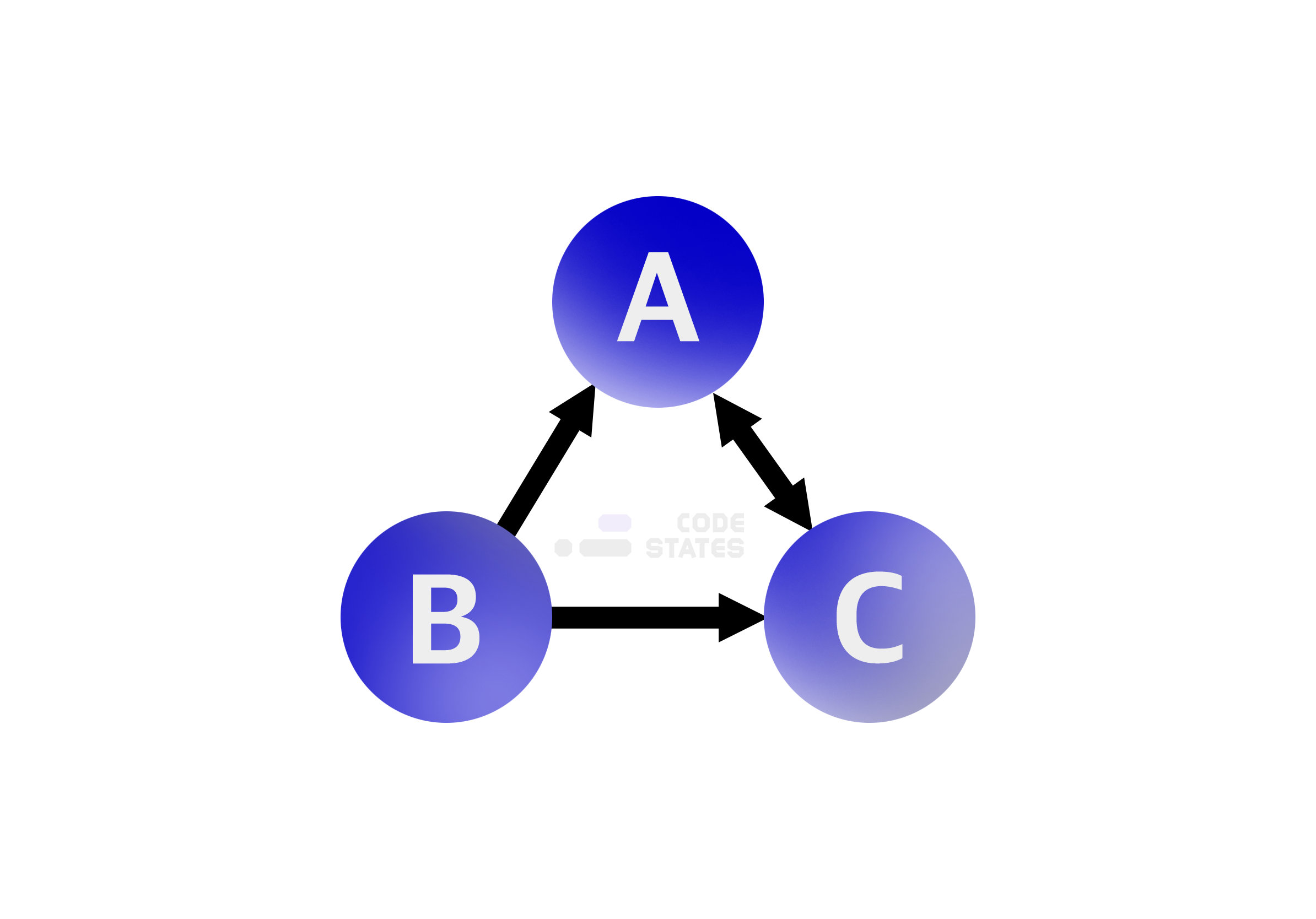
• A의 진출차수는 1개임: A -> C
  - [0][2] == 1
• B의 진출차수는 2개임: B -> A, B -> C
  - [1][0] == 1
  - [1][2] == 1
• C이 진출차수는 1개임: C -> A

인접 행렬을 사용할 때

• 한 개의 큰 표와 같은 모습을 한 인접 행렬은 두 정점 사이에 관계가 있는지 없는지 확인하기에 용이
  - 예를 들어 A에서 B로 진출하는 간선이 있는지 파악하기 위해선 0번째 줄의 1번째 열에 어떤 값이 저장되어 있는지 바로 확인할 수 있음
• 가장 빠른 경로(shortest path)를 찾고자 할 때 주로 사용됨

인접 리스트

인접 리스트는 각 정점이 어떤 정점과 인접한느지를 리스트의 형태로 표현함. 각 정점마다 하나의 리스트를 가지고 있으며, 이 리스트는 자신과 인접한 다른 정점을 담고 있음.

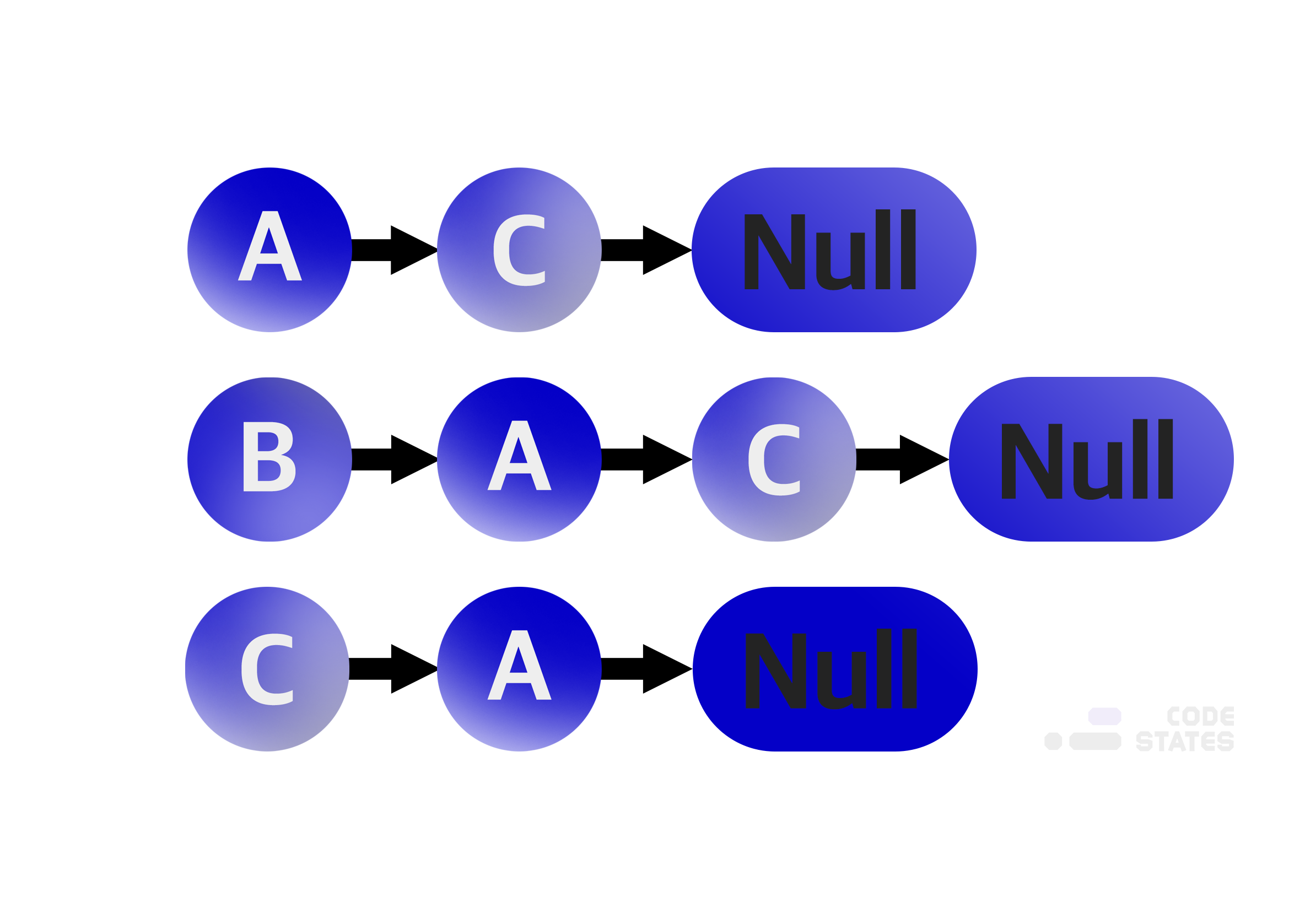
B는 A와 C로 이어지는 간선이 두 개가 있는데, 왜 A가 C보다 먼저인가? 순서는 중요한가?

보통은 중요하지 않음. 그래프, 트리, 스택, 큐 등 모든 자료 구조는 구현하는 사람의 편의와 목적에 따라 기능을 추가/삭제 할 수 있음. 그래프를 인접 리스트로 구현할 때, 정점별로 살펴봐야 할 우선 순위를 고려해 구현할 수 있음. 이 때, 리스트에 담겨진 정점들을 우선 순위별로 정렬할 수 있음. 우선 순위가 없다면 연결된 정점들을 단순하게 나열한 리스트가 됨.

인접리스트는 언제 사용할까?: 메모리를 효율적으로 사용하고 싶을 때

Graph의 실사용 예제

예. 포털 사이트의 검색 엔진. SNS에서 사람들과의 관계. 네이게이션.

서울에 사는 A. 대전에 사는 C. 부산에 사는 B. A는 C를 태워 B를 보러가려 하는 상황.

• 정점: 서울, 대전, 부산
• 간선: 서울-대전, 대전-부산, 부산-서울

서울, 대전, 부산 사이에 간선이 존재하는데, 이 간선은 네이게이션에 이동할 수 있음을 나타냄. 정점에 캐나다의 토론토를 추가한다면 자동차로는 토론토에서 한국으로 이동할 수 없기 때문에 어떠한 간선도 추가할 수 없음. -> 그래프에선 이런 경우를 관계가 없다고 표현함.
서울, 대전, 부산이 서로 관계가 있다는 것은 알 수 있지만, 각 도시가 얼마나 떨어져 잇는지는 알 수 없음. 간선은 특정 도시 두 개가 이어져 있다는 사실만 알려줄 뿐, 그 외의 정보는 포함하지 않고 있음. 이렇게 추가적으로 정보를 파악할 수 없는 그래프, 가중치(연결의 강도가 얼마나 되는지)가 적혀 있지 않은 그래프를 비가중치 그래프 라고 함.

/*
	1 == 서울, 2 == 부산, 3 == 대전
	0은 연결되지 않은 상태, 1은 연결된 상태 (간선을 정수로 표현)
*/

[1] = [0, 1, 1] // 서울 - 부산 , 서울 - 대전
[2] = [1, 0, 1] // 부산 - 서울 , 부산 - 대전
[3] = [1, 1, 0] // 대전 - 서울 , 대전 - 부산

위 정보만으로는 서울에서 부산까지 갈 수 있다는 사실 외에 파악할 수 있는 정보는 없음. 현재의 비가중치 그래프를 가중치 그래프로 바꾸고 각 도시 간의 거리를 표시한다면 더 자세한 정보를 담을 수 있음.

• 정점: 서울, 대전, 부산
• 간선: 서울-140km-대전, 대전-200km-부산, 부산-325km-서울

알아둬야 할 그래프 용어들

• 정점(vertex): 노드(node)라고도 하며 데이터가 저장되는 그래프의 기본 원소
• 간선(edge): 정점 간의 관계를 나타냄 (정점을 이어주는 선)
• 인접 정점(adjacent vertex): 하나의 정점에서 간선에 의해 직접 연결되어 있는 정점
• 가중치 그래프(weighted graph): 연결의 겅도가 얼마나 되는지 적혀져 있는 그래프
• 비가중치 그래프(unweighted graph): 연결의 강도가 적혀져 있지 않은 그래프
• 무(방)향 그래프(undirected graph): 위에 네비게이션 예제는 무(방)향 그래프임. 서울에서 부산으로 갈 수 있듯, 반대로 부산에서 서울로 가는것도 가능함. 하지만 단방향(directed) 그래프로 구현된다면 서울에서 부산을 갈 수 있지만, 부산에서 서울로 가는 것은 불가능함. 만약 두 지점이 일방통행 도로로 이어져 있다면 단방향인 간선으로 표현할 수 있음.
• 진입차수(in-degree)/진출차수(out-degree): 한 정점에 진입(들어오는 간선)하고 진출(나가는 간선)하는 간선이 몇 개인지를 나타냄.
• 인접(adjacency): 두 정점 간에 간선이 직접 이어져 있다면 이 두 정점은 인접한 정점임
• 자기 루프(self loop): 정점에서 진출하는 간선이 곧바로 자기 자신에게 진입하는 경우 자기 루프를 가졌다 라고 표현함. 다른 정점을 거치지 않는 것이 특징임
• 사이클(cycle): 한 정점에서 출발하여 다시 해당 정점으로 돌아갈 수 있다면 사이클이 있다고 표현함. 네비게이션 그래프는 서울 -> 대전 -> 부산 -> 서울로 이동이 가능하므로 사이클이 존재하는 그래프임.

연습 문제 - 그래프 구현

import java.util.*;

public class Solution { 
	private String value;
  private ArrayList<Solution> children;

  public Solution() {	//전달인자가 없을 경우의 생성자
    this.value = null;
    this.children = null;
  }
  public Solution(String data) {	//전달인자가 존재할 경우의 생성자
    this.value = data;
    this.children = null;
  }

  public void setValue(String data) {
    this.value = data;
  }

  public String getValue() {      //현재 노드의 데이터를 반환
    return value;
  }
  public void addChildNode(Solution node) {
    if(children == null) children = new ArrayList<>();
    children.add(node);
  }
  public void removeChildNode(Solution node) {
    String data = node.getValue();

    if(children != null) {
      for(int i = 0; i < children.size(); i++) {
        if(children.get(i).getValue().equals(data)) {
          children.remove(i);
          return;
        }
        if(children.get(i).children != null) children.get(i).removeChildNode(node);
      }
    }
  }

  public ArrayList<Solution> getChildrenNode() {
    return children;
  }

  public boolean contains(String data) {      //재귀를 사용하여 값을 검색합니다.
    if(value.equals(data)) return true;

    boolean check;

    if(children != null) {
      for(int i = 0; i < children.size(); i++) {
        check = children.get(i).contains(data, false);
        if(check) return true;
      }
    }
    return false;
  }

  public boolean contains(String data, boolean check) {      //재귀를 사용하여 값을 검색합니다.
    if(value.equals(data)) return true;

    if(children != null) {
      for(int i = 0; i < children.size(); i++) {
        check = children.get(i).contains(data, check);
      }
    }
    return check;
  }
}