현재 하고 있는 일은 보험사의 보험사기 건을 적발하는 모델링을 하고 있다.
Goal 1. 의심 상위 유저에 대한 적발율 올리기
Goal 2. 보상 금액을 최소화하는 모델링
2가지를 하고 있는데 1번은 어느정도 완료가 되어 1번 과정에서 적용한 방법들을 블로그에 남긴다.
FDS 를 하다보면 Fraud 클래스가 Normal 클래스 대비 매우 소수인 경우가 많다.
이 경우 모델을 Cross Entropy로 학습하면 단점이 있는데, Recall 수치가 아주 낮게 나온다는 단점이 있다. 이 현상을 Under Estimate 라고 부르면 무리가 있으려나..., 일단 확실히 Less Focus 하는 경향은 확인된다.
왜냐하면 다수 클래스에서 C-E 로스 값을 줄이는 방향이 소수 클래스에서 C-E 로스 값을 줄이는 것보다 전체 로스 합의 관점에선 당연한 방향이기 때문이다.
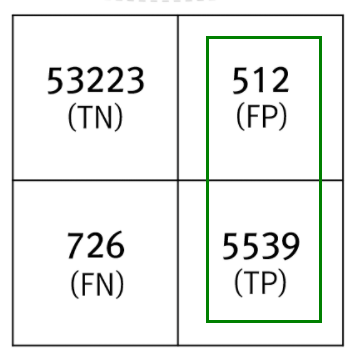
( Fraud Class가 소수 클래스라면 FP 의 수가 FN에 비해 매우 낮을 것이다. TP는 매우매우 적고... )
이러한 문제를 해결하기 위해선,
1. 언더/오버 샘플링 하여 클래스간 불균형을 줄이거나 없애기 ( 제일 흔하다 )
2. Focal Loss 적용 등의 방법이 있다.
그 외 방법은 (특히 Boosting 모델에서) 아직 모르겠다. ( Soft Label - Psuedo Learning은 해당 프레임워크에서 타겟 값이 확률값은 지원 안해줘서 불가능한 것으로 알고 있다. )
실제 내가 적용한 방법으로 아래 2가지를 섞은 Weighted Focal Loss를 적용했다.
( 매우 간단히 적용 가능하다. )
그 외로 오버 샘플링은 효과가 없었고 언더 샘플링은 아주 미미한 성능 향상이 있었으나 직관적으로(통계적으로도) 유의미 하지 않은 수치였다.
- Weighted Cross Entropy
-
소수 클래스에 가중치(보통 상수, n이라고 하자)를 더 부가하여 gradient(penalty)를 n배 부과함 ( 페널티가 커짐에 따라 모델 학습시 소수 클래스에 Focus 되는 효과가 존재 )
-
한계점 : 다수/소수 클래스 관점에서 벗어나, 분류하기 힘든 Case에 대해서 모델 학습시 Focus하는 효과는 가지기 힘듦
- Focal Loss
-
자세한 설명은 생략
( 다른 블로그의 좋은 설명 : https://gaussian37.github.io/dl-concept-focal_loss/ ) -
기본적인 컨셉은 분류하기 힘든 Case에 대해서 penalty를 크게 부과하여 모델 학습시 해당 Case를 Focus한다.
-
어떻게? : gradient 와 penalty에 확률과 관련된 가중치를 가하여, 정답 클래스가 1이라면 확률 p가 1에 가까우면 작은 페널티를, 0에 가까우면 큰 페널티를 부가한다.
-
구체적인 적용 방법
grad : (y-p) 였던걸, 다음과 같이 변경한다.if target == 1, (1-p) x (y-p) elif target == 0, p x (y-p)로 부가한다면, 타겟이 1인 경우에 대해서 확률을 높게 output이 나온다면 잘 학습된 것이므로 작은 페널티(1-p) 를 부가한다.
-
다음으로 hessian : 위 grad를 x 에 대해서 편미분 해주면 된다.
참고 : https://stats.stackexchange.com/questions/231220/how-to-compute-the-gradient-and-hessian-of-logarithmic-loss-question-is-based
f = p x (y-p) = py - p^2
df / dx = ( df / dp ) * ( dp / dx ) 이다.
df / dp = y - 2p
dp / dx = p(1-p)
따라서 df / dx = (y-2p)p(1-p) 이다. ( 계산 실수가 있을수도 있다.. )
여기서 y = 1 이다. ( target = 1 이라서 grad 는 (1-p)x(y-p) 였다. )
최종적으로 target = 1 일때 hessian 은 (1-2p)p(1-p) 이다.
이걸 코드로 표현하면 다음과 같다. ( CatBoost 적용 )
import math
from six.moves import xrange
class LoglossObjective(object):
def calc_ders_range(self, approxes, targets, weights):
assert len(approxes) == len(targets)
if weights is not None:
assert len(weights) == len(approxes)
result = []
for index in range(len(targets)):
e = np.exp(approxes[index])
p = e / (1 + e)
der1 = targets[index] - p
der2 = -p * (1 - p)
if (targets[index] == 0.0) & (p<0.5):
# 타겟 값이 정상 유저인데, 정상이라고 판단한 경우 ( True Negative )
der1 = (p)*(targets[index] - p)
der2 = (1-2*p)*(-p * (1 - p))
elif (targets[index] == 0.0) & (p>=0.5):
# 타겟값이 노말 유저인데,fraud 라고 예측한 경우 ( False Positive )
der1 = 3*(p)*(targets[index] - p)
der2 = 3*(1-2*p)*(-p * (1 - p))
elif (targets[index] > 0.0) :
# 타겟 값이 fraud 이라면 p값이 높을수록 (정답에 가까울수록) 페널티가 적도록 세팅. 추가로 3배 페널티
der1 = 3*(1-p)*(targets[index] - p)
der2 = 3*(2*p-1)*(-p * (1 - p))
if weights is not None:
der1 *= weights[index]
der2 *= weights[index]
result.append((der1, der2))
return result소수 클래스에 대해서 우리가 목적하는 바를 달성하기 위해서 Tuning의 절차로,
위에서 p 를 곱할것이나 p^2 을 곱할것이냐 p^1.5 를 할것이냐는 해봐야 한다.
( p 의 승수가 올라갈수록 맞추기 어려운 케이스에 더 집중한다. 하지만 이게 꼭 우리가 바라는 대로 동작하진 않는다. )
위에서 n 을 1로 하냐 2로 하냐 3으로 하냐 ... 등도 해봐야 어떤게 제일 좋은 성능을 내는지 알 수 있다.
이렇게 Focal Loss 를 적용하면 단점도 있다.
1. Loss Func 내 분기점이 많아지고, (CatBoost)프레임 워크상에서 병렬연산을 지원해주지 않아서 학습 속도가 매우 느려진다.
2. model output 이 proba 확률값이 더이상 아니게 된다. 그리고 기존 output 대비 매우 Over Estimate 하게 된다.
그럼에도 불구하고 목적에 맞는 model을 학습시킬 수 있었다.
( 목적 : Fraud 의심 상위 30% 유저 내 적발율 상승 )
실제로 위 목적 기준으로 봤을때 기존 모델의 65% 에서 76%로 상승했고, 다른 딥러닝 SOTA 모델 앙상블한 결과보다 같거나 높은 성능을 보여줬다.
이후 CatBoost 실행 코드는 다음과 같다.
( 실제 업무에서 적용한 p의 승수, n가중치, focal 미분/편미분 값은 아래 코드와 다르다. )
%%time
from catboost import CatBoostClassifier, Pool
for i in range(n_splits):
print('='*20, str(i+1), '='*20)
cat_feat_ls = []
for item in list(data[cat_cols].select_dtypes(include='category').columns):
cat_feat_ls.append(item)
cat_features = cat_feat_ls
train_data = globals()[f'train_feat_{i+1}']
train_labels = globals()[f'train_label_{i+1}']
valid_data = globals()[f'valid_feat_{i+1}']
valid_labels = globals()[f'valid_label_{i+1}']
globals()[f'CatB_model_{i+1}'] = CatBoostClassifier(iterations=15000,
depth=12,
thread_count=12,
learning_rate=1e-3,
loss_function=LoglossObjective(),
eval_metric='PRAUC',
early_stopping_rounds=400,
verbose=1000)
# train the model
globals()[f'CatB_model_{i+1}'].fit(train_data, train_labels, cat_features, eval_set = (valid_data,valid_labels))
globals()[f'CatB_model_{i+1}'].save_model(f'CatB_C_Penalty_v6_fold_{i+1}')
print(str(i+1),'fold model saved')여기서 Eval_metric 는 Precision Recall 커브의 아래 면적인데, True Negative 케이스가 압도적으로 많은 클래스 불균형 데이터 학습시 참고할만한 평가지표 이다.
다만, 꼭 높은 성능을 의미하진 않고 다른 평가지표 n개 ( ex. AUC, MCC ..., F1, F2 ) 등으로 n개 모델 학습 후, 제일 성능이 잘나온 모델을 채택해야 한다.
- 많이 도움이 되었던 공식 문서는 H2O 프레임워크 공식 문서였다. ( 오히려 과분할만큼 너무 자세하다 https://docs.h2o.ai/h2o/latest-stable/h2o-docs/performance-and-prediction.html )
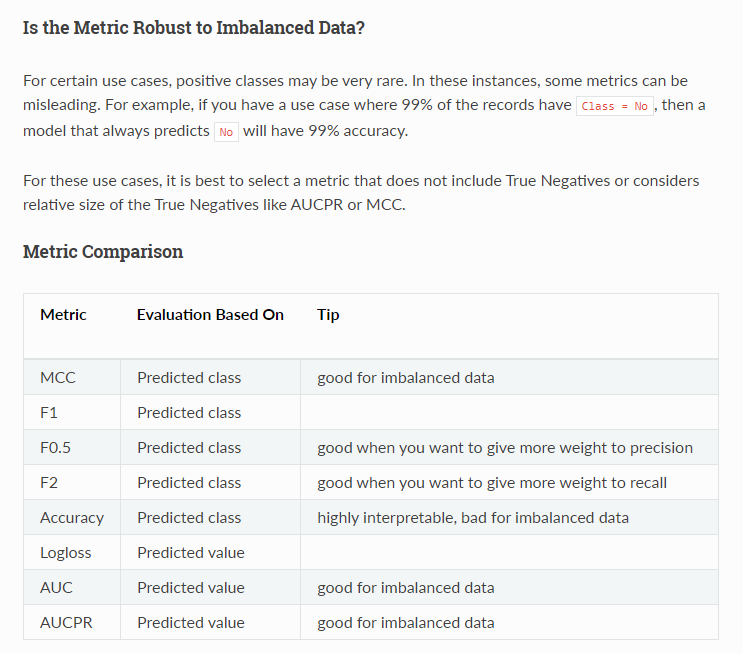
(나의 경우) 현재 풀고있는 데이터는 대략 99% 정상 유저와 1% 사기 유저인데, AUC 평가 지표가 (회사에서 원하는)성능이 제일 좋은것으로 나타났다.
며칠전, 데이터야놀자 배민 허위리뷰 발표에서 LGBM 에서 Focal Loss + (TomekLink+)OverSampling 을 썼다기에 (구체적으로 적용방법을 공유하면 좋겠다 싶어) 올리는 글.