[기초통계] 카이스퀘어 분포

2400·2022년 6월 4일

( 교과 과정에서 )
t 분포를 배우고 난 뒤 > 카이스퀘어 분포를 배우고 > F 분포를 배운다.

카이.. 라는 용어는 그리스어인데 용어부터 우리에게 익숙치 않다.

이걸 단순히 x 라고 보고 이 x가 키, 몸무게일수도 있는데 하여튼 임의의 x가

(자연의 대부분의 변수-키,몸무게-처럼) 는 정규 분포를 따른다고 하자.

그러면 이 x(카이)가 정규분포라고 하면, x^2는 무슨 분포를 띌까? 가 아주 중요한 질문이다.

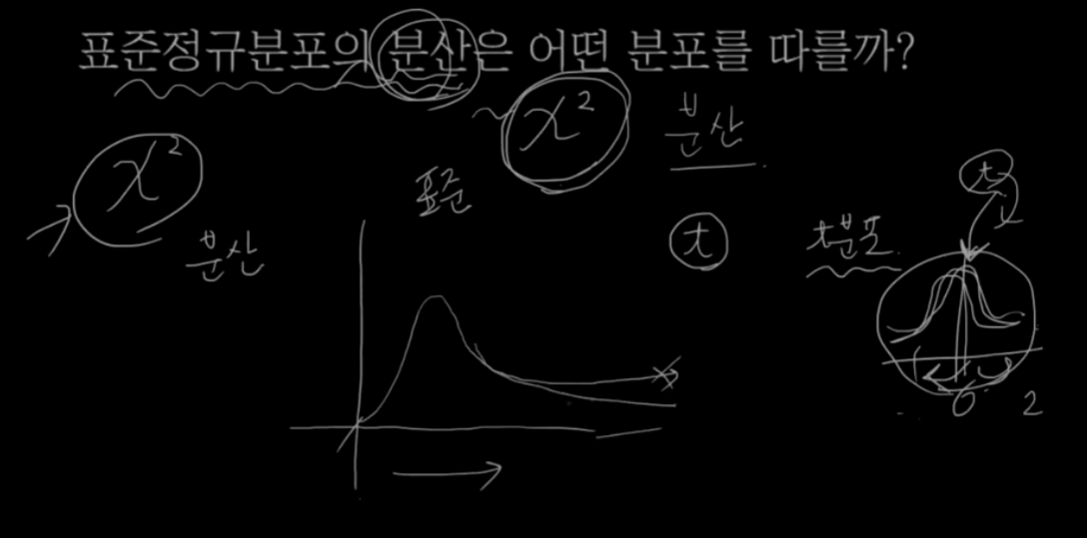
표준정규분포의 분산 = x 이다.

표준정규분포의 분산은 어떤 형태를 띌까?
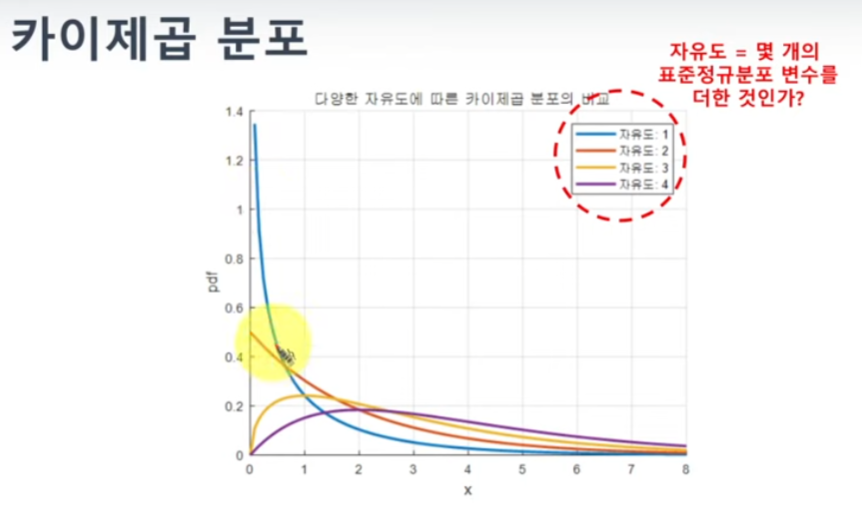
자유도 값에 따라 분포의 모양이 달라질 수 있지만 대충 이런식으로 생겼다.

그러면 (분포를 알고나면) 카이스퀘어 값이 주어졌을때, 이 값이 대충 큰지 작은지 판단할 수 있다.

카이스퀘어 분포의 피크점(평균 부근)은 대략 자유도 값 부근 점인데,

자유도가 20, 카이스퀘어 값이 20이라면 아, 대략 분포의 평균 근처구나 하고 알 수 있다.

=====

정의만 봐서는 무슨 말인지 모르겠다.

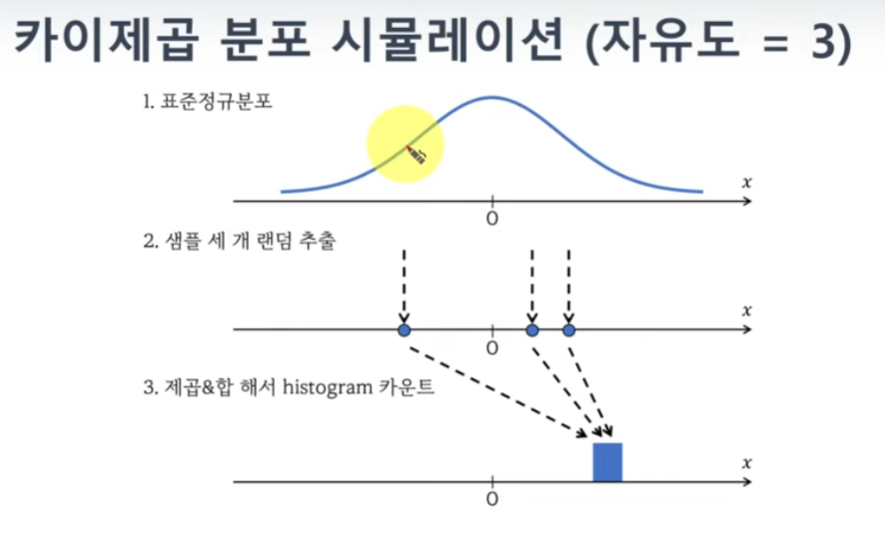
자유도에 따라 분포가 다르게 나오는건
시뮬레이션을 통해 납득할 수 있다.

한마디로 오차나 편차를 분석할 때 도움이 된다.

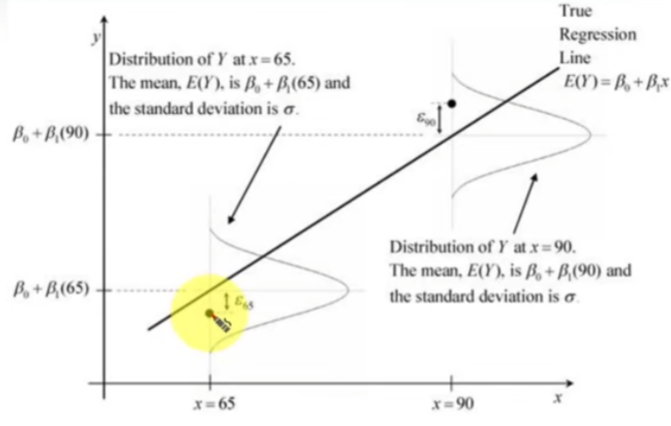
실제값과 예측 값의 차이를 분석할 때,

오차들의 제곱합을 쭉 더해준게

이 모델의 전체적 오라차고 한다면

이 경우 카이제곱 분포를 활용한다면

모델링에 도움이 될 것이고
이 오차가 정말로 큰지 판단이 가능함

결론적으로 카이스퀘어 검정을 통해

오차를 검정가능하고

그 오차가 우연히 발생한 것인지, 아니면 숨겨진 의미가 있는 오차인지 판단할 수 있음.

크게 2가지 검정 존재.

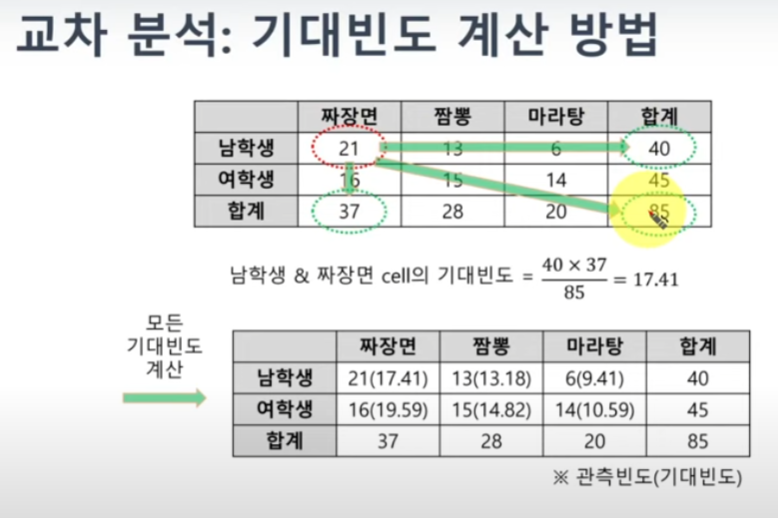
보통 많이 보는건 교차 분석.

식을 보면 오차값의 제곱을 해준건데, 기대값을 나누어줌으로써 정규화를 시켜줬다. 라고 이해하면 된다.

공부용 혹은 정리용 혹은 개인저장용