[LGBM] 알고리즘
출처 : 04-8: Ensemble Learning - LightGBM (앙상블 기법 - LightGBM)
고려대학교 산업경영공학부 DSBA 연구실
https://www.youtube.com/watch?v=4C8SUZJPlMY&t=499s

전통적인 GBM 모형은, 모든 피쳐&객체에 대해서 스캔을 쭉 한 다음 Info gain을 측정함.
모든 피쳐에 대해서 수행
모든 객체에 대해서 수행
-> 시간이 오래 걸린다
따라서 XGB에서는 병렬처리의 목적으로, 전체를 bucket 단위로 쪼갠다음 bucket 안에서 최적의 스플릿 지점을 찾는다.
모든 데이터 객체를 스캔하는 문제를 완화했는데
LGBM에선
모든 데이터 포인터를 스캔하지 않기 위해서 그래디언트 기반의 One side 샘플링 (GOSS)를 함.
( XGB 에서는 데이터를 뭉텅이로 잘라서 buckets를 만들고 그 안에서 최적의 split을 찾는데 그 방법의 대안으로서 GOSS는 피쳐별로 Gradient를 구해서 정렬한 다음 상위 n%는 100% 활용하고 하위 n%는 랜덤하게 선택함
추가 설명 :
여기 설명에서 데이터 객체란 df의 row에 해당하는 것 같다.
(출처 : https://aldente0630.github.io/data-science/2018/06/29/highly-efficient-gbdt.html )
LGBM GOSS를 쭉 읽어보니,
계산량을 줄이기 위해서
row별 gradient를 계산하여 상위 a% 데이터는 그대로 사용하고 사용된 a%를 제외한 1-a % 데이터에 대해서 일부(b%)만 랜덤 샘플링한 다음 이렇게 랜덤 샘플링한 데이터에서 얻어지는 gradient를 (1-a/b)만큼 overweight 하여서 전체 데이터 분포를 바꾸지 않으면서 연산량을 줄이는 방법이다.
(GBM)
사전 정렬 알고리즘으로 사전 정렬한 변수 값에 대해 가능한 모든 분할점을 나열한다. 이 알고리즘은 간단하며 최적 분할점을 찾아낼 수 있지만 훈련 속도와 메모리 소비 모든 면에서 비효율적이다.
(XGboost)
히스토그램 기반 알고리즘이 있다. 정렬한 변수 값에서 분할점을 찾는 대신 히스토그램 기반 알고리즘은 연속적인 변수 값을 개별 구간으로 나누고 이 구간을 사용하여 훈련 시 변수 히스토그램을 만든다. 히스토그램 기반 알고리즘은 메모리 소비와 훈련 속도에서 보다 효율적이므로 이를 바탕으로 작업을 진행했다. 알고리즘 1에 적힌 대로 히스토그램 기반 알고리즘은 변수 히스토그램을 기반으로 최적 분할점을 찾는다. 히스토그램 만드는 일에
O (num_of_datas × num_of_features), 분할점 찾는 일에 O(n_bins ×num_of_features)
가 필요하다. #bin은 대개 #data보다 훨씬 작기 때문에 히스토그램 만드는 일이 계산 복잡도를 좌우한다. #data 또는 #feature를 줄인다면 GBDT 훈련은 상당히 빨라질 것이다.
AdaBoost에서의 표본 가중치는 각 데이터 개체의 중요도를 알려주는 좋은 지표이다. 그러나 GBDT의 경우 표본 기본 가중치가 없으므로 AdaBoost에 제안된 표본 추출 방법을 직접 적용할 순 없다. 다행히도 GBDT에서 각 데이터 개체에 대한 기울기는 데이터 표본 추출에 유용한 정보를 제공한다. 즉, 개체의 기울기가 작다면 해당 개체에 대한 훈련 오차가 작고 이미 잘 훈련된 것이다. 단순한 아이디어는 기울기가 작은 데이터 개체를 버리는 것이다. 그러나 그렇게 하면 데이터 분포가 바뀌므로 학습 모형의 정확도를 저하시킬 수 있다. 이 문제를 피하기 위해 기울기 기반 단측 표본 추출(GOSS)이라는 새로운 방법을 제안한다.
)
두번째로 모든 피쳐에 대해서 효율적으로 수행하기 위해 Exclusive Feature Bundling 을 함.
각 방법론에 대해서 핵심 아이디어를 살펴보자면
GOSS는 개별 데이터에 대해 서로 다른 Gradient를 가지고 있는 객체이기 때문에 어느 지점을 스플릿해야 하는지 계산하기 위해서 다른 역할을 한다.
Gradient가 크면 클수록 중요한 객체인데,
그래디언트가 큰건 킵하고 작은건 랜덤하게 드랍한다.
1000개 데이터라면 그래디언트가 높은 상위 n 개는 킵하고 나머지는 랜덤하게 제외함
EFB에 깔린 가정은 원핫인코딩과 같이 피쳐가 sparse한 경우 almost 상호배반적인다.
어떤 하나의 객체에 대해서 특정 2개의 변수가 non-zero 값을 가질 경우가 드물다
하나의 객체 내에서 2개 이상의 변수들이 0이 아닌 값을 동시에 가질 가능성이 많은 변수가 많다. 대표적으로 원핫 인코딩
Exclusive 피쳐들을 하나의 변수로 변환한다. (번들링)
잠재적인 문제점으로 Exclusive 하지 않은 변수들도 하나의 변수로 변환하는 부작용이 있을수도 있다.
====
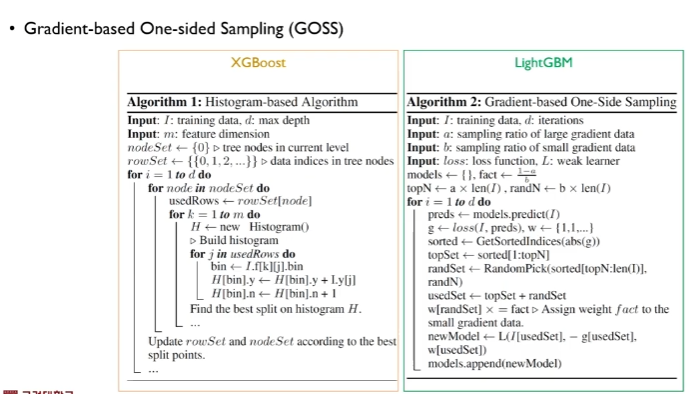
왼쪽은 Hist based ( bucket )을 통해 최적의 스플릿 포인트를 찾는 방식의 알고리즘
우측은 GOSS

GOSS 자체는 간단함
그래디언트가 가장 높은 값부터 낮은 값까지를 계산하여 정렬시킬 수 있음
그러면 큰 그래디언트쪽에 대해선 Top a * 100 % 인스턴스는 보존을 함. 전부 사용
반면에 스몰 그래디언트에 대해선 랜덤하게 b * 100% 인스턴스를 선택하게 됨
1-a / b 를 1보다 크게 잡으면 효과가 크다고 한다
a 를 상위 10%가 되도록 0.1
b 를 하위 90%가 되도록 0.9 라고 해보자
그럼 0.9/0.9 = 1 이되는데
이 의도를 극대화 하기 위해 a를 0.05 로,
b를 하위 50%가 되도록 0.5라고 해보자
그럼 0.95/0.5 = 19 > 1 이 됨
GOSS는 하이퍼파라미터 a,b를 어떻게 정하느냐에 따라 성능이 결정됨. 내용 끝.
====
모든 변수를 탐색하는게 시간이 오래 걸리니
EFB 방법에 대해 설명
EFP의 2가지 절차
- Greedy Bundling : 현재 존재하는 피쳐 셋에 대해서 어떤 피쳐들을 하나의 번들로 묶을지 결정함
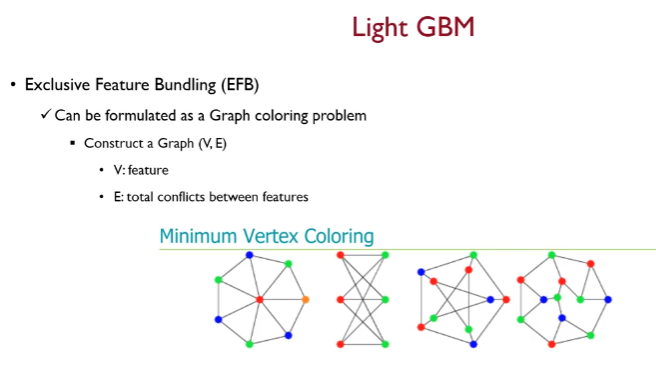
처음 EFB 에서 번들을 찾는 것 :
그래프 색칠 문제
변수들간에 그래프로 그림
노드는 피쳐가 되고 엣지는 두 피쳐들 간에 conflict 를 의미함
결국 confilict 가 많은 애들은 번들링되면 안되고
conflict를 non-zero 값을 갖는 비율로 정의할 수 있음
컨플릭트가 없는 애들은 번들링 가능
이미지에서 색깔별로 번들링이 가능함.
미니멈 Vertex Coloring은 대표적인 np hard 문제인데
따라서 greedy bundling을 진행함
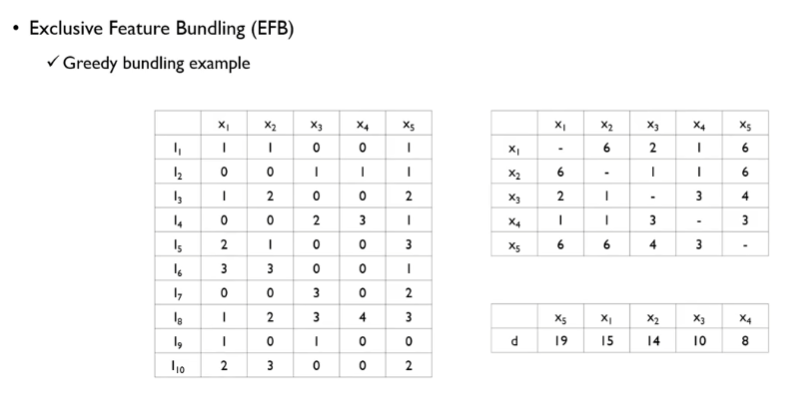
두 노드간 엣지의 강도를 표현해야 함
동시에 0이 아닌 객체의 수로 edge를 정의함
x1, x2는 좌측의 표에서 총 6개의 0이 아닌 객체가 있음
x2, x3은 동시에 0이 아닌 객체는 1개밖에 없음.
위 방법으로 x1~x5에 대해서 내림차순하여 강도(degree)를 정의함
이런식으로 degree를 내림차순 한 다음,
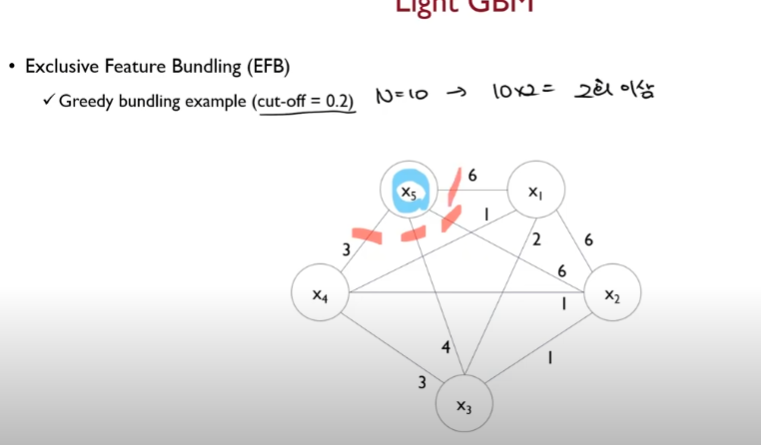
cut off hyper param 0.2라면
N=10 일때 10*0.2 = 2
2 이상의 엣지를 끊어버림

x5 는 고립되버림
이후 x1에 대해서,
2 이상의 엣지를 끊어버리면
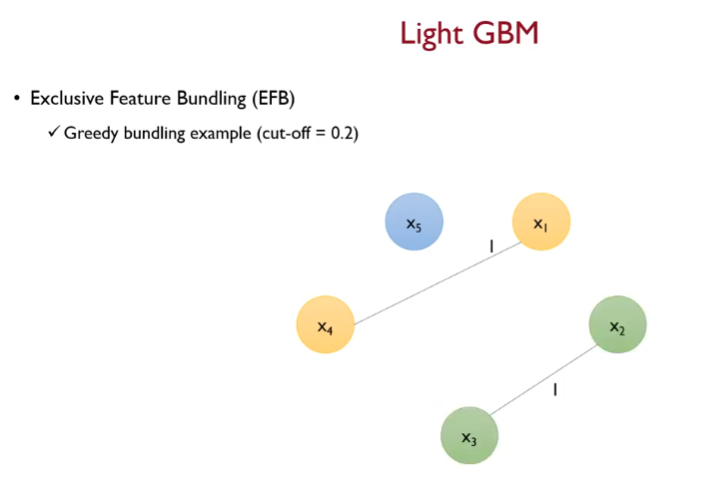
최종적으로
x1~x5 에 대해서 3개로 번들링됨
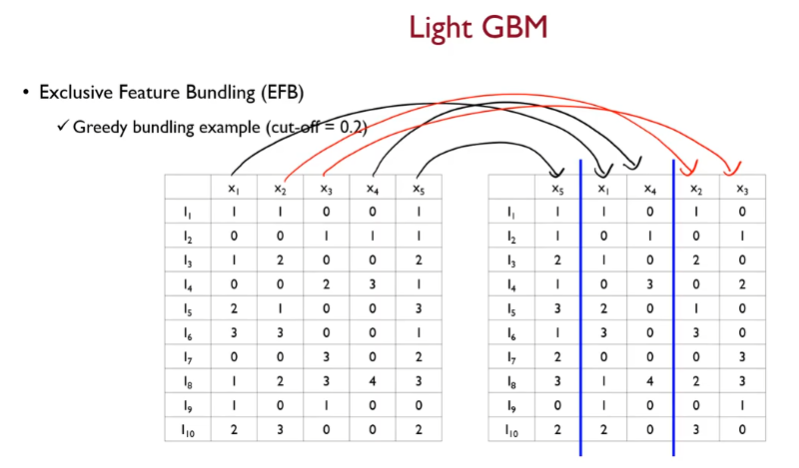
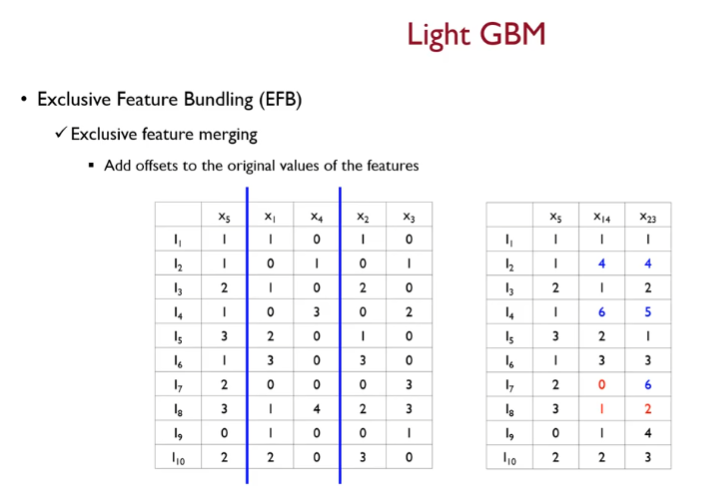
이후 머지 진행
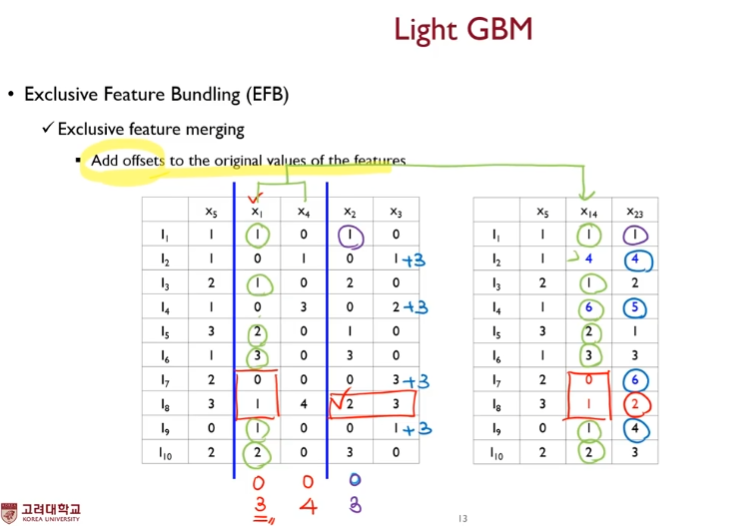
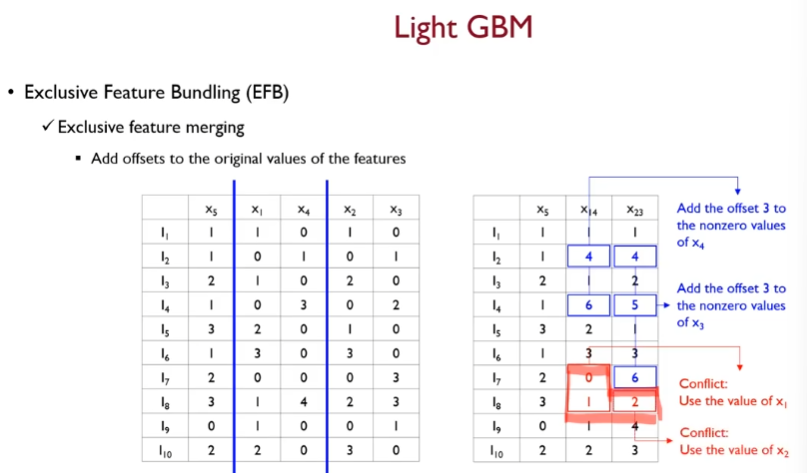
offset을 더한다.
여기서 offset이란
기준 변수에다 해당 변수가 가질 수 있는 최대값을 더해줌
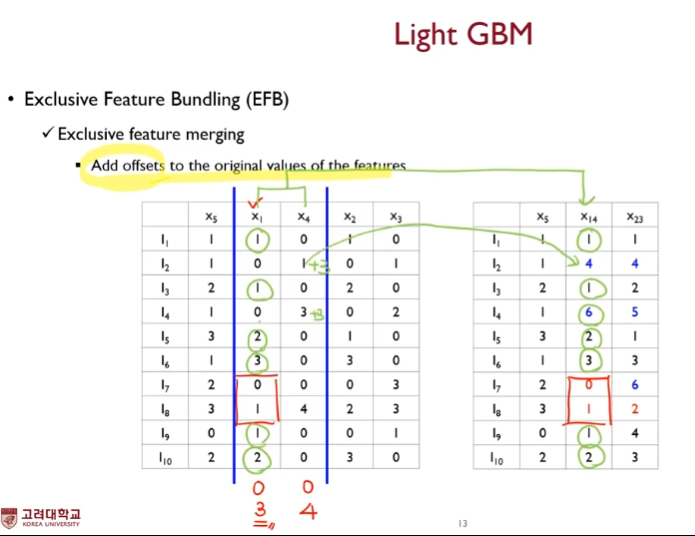
머지 알고리즘을 보아하니
- 기준 변수의 값이 0이 아니고 머지 대상의 변수의 값이 0인경우 기준 변수의 값을 그대로 넣는다.
- 만약 기준 변수의 값이 0인 경우 기준 변수의 최대값 + 머지될 변수의 값을 더하여 넣는다.
- 만약 기준 변수의 값이 0이 아닌데 머지 대상의 변수의 값 또한 0이 아니라면, 또는 둘 다 0인 경우( conflict 상황 ) 기준 변수의 값을 그대로 사용한다.