어떤 기준에 의하여 그룹을 A,B로 구분했습니다.
저는 현재 그룹 A가 의심스럽습니다.
그룹 A에선 어떤 이벤트가 발생할 확률이 50% 이기 때문입니다.
일반적인 그룹 B에선 어떤 이벤트가 발생할 확률이 20% 입니다.
20% 대비 50%는 너무 높은 확률 아닌가요?
느낌적으로 이상하다고 느껴집니다.
통계학 책의 어디선가 봤던 "오즈" 그리고 "오즈비"로 표현해보겠습니다.
그룹 A의 오즈는 확률이 50% 이므로 0.5 / 1-0.5 = 1 입니다.
그룹 B의 오즈는 확률이 20% 이므로 0.2 / 1-0.2 = 1/4 입니다.
이 두 그룹의 오즈비는 4 입니다.
오즈비로 봐도 의심스럽습니다.
그런데 저는 오즈비를 구하면서 신경쓰이는 점이 있습니다.
그룹 A의 샘플 개수가 총 20개로 매우 적다는 점입니다.
우연 아닐까? 라는 생각도 듭니다.
이런 경우, 로그 오즈비의 신뢰구간으로 "충분히" 이상한지 아닌지를 확인할 수 있습니다.
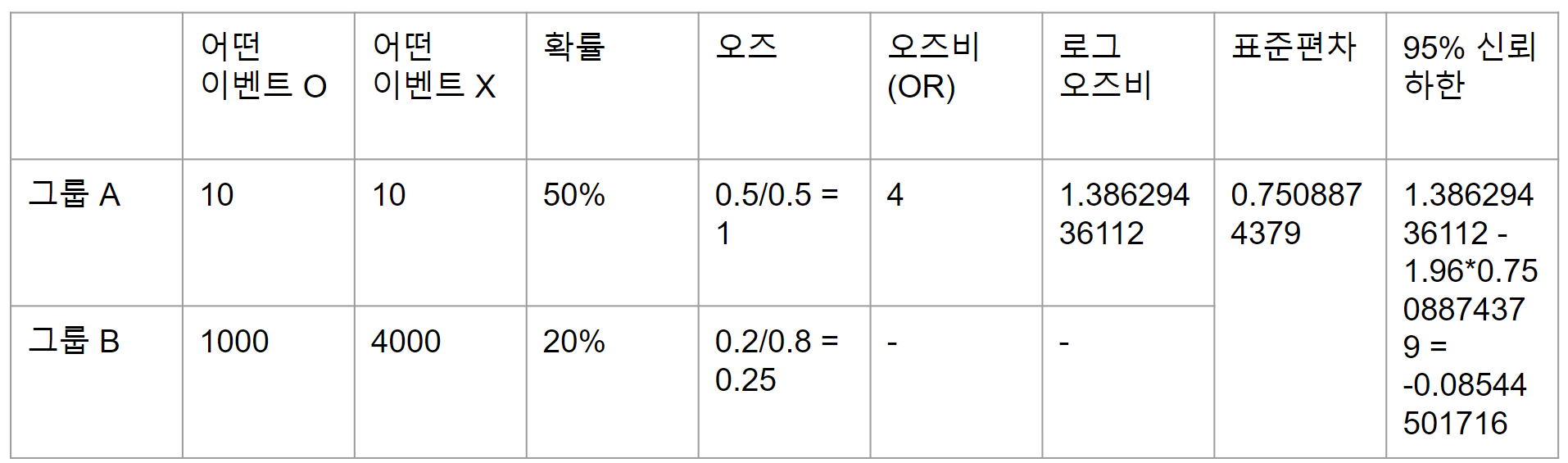
위 상황을 표로 그려보면 위와 같습니다.
오즈비는 4이므로 ln(4) = 1.38 입니다.
그리고 로그 오즈비에 대한 표준 편차는 각 하위 그룹의 샘플수의 0.5승의 역수의 합의 0.5승 입니다.
( 1/root(10) + 1/root(10) + 1/root(1000) + 1/root(4000) )**0.5 = 0.75 쯤 됩니다.
이 경우 신뢰 하한은 음수가 나오네요.
95% 신뢰 구간내에 0이 존재합니다.
이럴수가, 이상하긴 한데 아주 이상하지는 않다는 결론입니다.
그러면 데이터를 더 수집해서 아래 표의 결과를 얻었습니다.
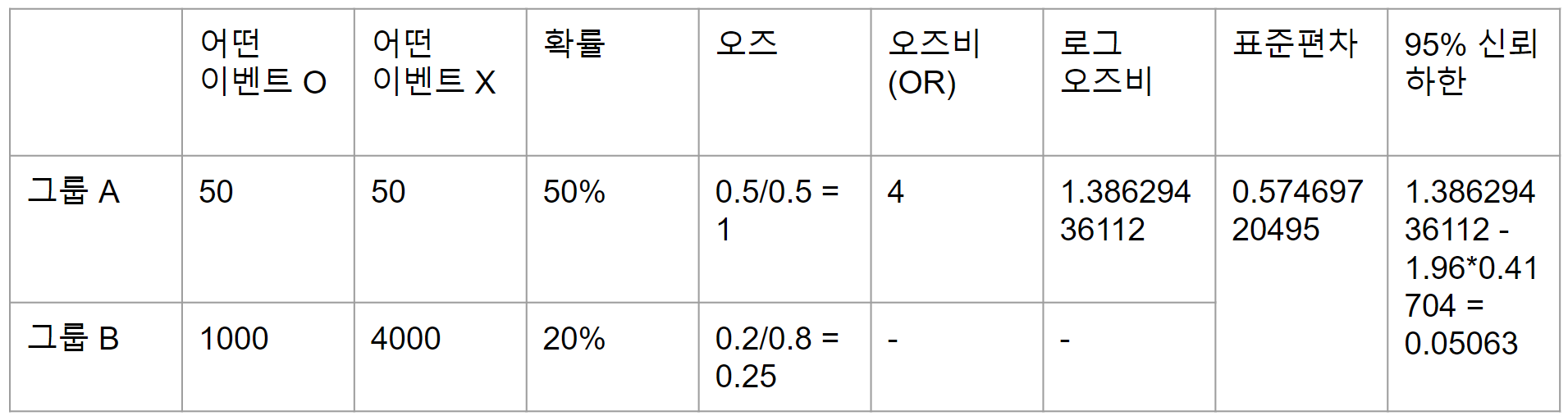
이 경우에선 신뢰 하한의 값이 0보다 큽니다.
즉 95%의 상황에서 발생하지 않는 아주 이상한 상황이라는 결론입니다.
이렇게 두 그룹의 어떤 확률에서 얼마나 유의미한 차이가 있는지 확인해보는
한가지 방법을 알아보았습니다.
