베이지안 사고와 일상적 추론
어느날 잠을 자다가 창문 밖을 보니 UFO 로 추정되는 무언가를 봤다.
이를 베이지안 스럽게 표현해보자.
- x : 지구상에서 발생하는 일
- H1 : UFO가 우리집 앞에 착륙했다.
- H2 : 영화 촬영 중이다.
Stage 1 :
- P(H1|x) = very low
- P(H2|x) = low
- 아무래도 지구에서, 그리고 우리 집 앞에 UFO가 착륙하는 사건은 발생하지 않을테니까 very low 한 확률일 것이다.
- 그나마 영화 촬영중이라면 가능성이 있겠지?
Stage 2 :
- 확률을 추정하는데 도움이 될 추가 데이터가 있다.
- D : 눈을 비비고 보니, 밝은 빛도 있고 접시 모양 물체도 있는데, 전선이 보이고 영화 제작진이 보인다.
- 이때
- P(H1|x,D) = very very low
- P(H2|x,D) = very High
위 사례에서 내가 내린 결론은 Data를 보다 더 잘 설명하는 가설은 H2이다.
-
왜? : P(H2|x,D) >>>>> P(H1|x,D) 이기 때문이다.
-
H 는 가설이고,
-
H 의 가능도 ( 그럴듯한 정도 )
= 추론을 할때 내가 가진 신념의 정도
= 이 신념의 정도는 세상 그리고 현상을 얼마나 잘 설명하고 있는지에 따라 다르기 때문이다, -
이를 역으로 설명하면
-
더 높은 그럴듯한 가설 -> 신념이 높고 -> 수학적으로 표현하면 확률의 비율 값이 높다.
-
여기서 확률의 비율이란
P(H2|x,D) / P(H1|x,D) 이다.

방금 예제에선 D 를 잘 설명하는 가설(신념)H를 고르는 방법을 설명했다.
위 예제에서 "데이터가 신념에 영향을 미친다."는 사실을 확인했다.
- 수집한 데이터에 따라 데이터를 잘 설명하는 신념으로 바꾼다.
반대로 신념은 데이터에 영향을 미치지 않는다.
- 자신이 가지고 있는 신념을 뒷받침할 데이터를 수집한다.
베이지안 사고는 자신의 신념을 바꾸고. 이해하고 있는 세상을 업데이트한다.
실제 세상을 잘 표현하는 가설을 얻을때까지 가설을 업데이트한다.
Quiz
어느날 퇴근하고 집에 들어와보니 창문이 깨져있고 현관문이 열려있다. 집에 들어가보니 노트북이 없다. 이를 수식적으로 표현해보자.
-
Data_1 : 문이 열려있고, 창문이 깨져있다.
-
Data_2 : 집에 들어가보니 노트북이 없다.
-
H1 : 집에 도둑이 들었다.
-
P(Data_1, Data_2 | H1 ) = High
-
그런데 이웃집 아이가 집에 와선 자초지종을 설명해주는데,
본인이 야구공을 잘못던져 창문을 깨트렸고,
문이 열려있어 들어왔었다.
노트북이 눈에 띄여 귀중품이라 자신이 잠시 보관하고 있었다고 한다. -
Data_3 : 아이가 찾아와 자초지종을 설명
-
H2 : 아이가 실수로 공놀이를 하다가~~~ (생략)
-
P(Data_1, Data_2, Data_3 | H2 ) = Very High
-
P(Data_1, Data_2, Data_3 | H1 ) = Low
- P(Data_1, Data_2, Data_3 | H2 ) / P(Data_1, Data_2, Data_3 | H1 ) >>>> 1
불확실성 측정
빈도주의 확률은 실제 문제 해결에 부적절한 경우가 많다.
- 내일 비가 올 확률은?
- 저건 UFO 인가?
친구랑 이야기를 하다가 "~~" 주제가 나무위키에 있냐/없냐로 내기를 하게 됐다.
- 나무위키에 없다.에 100달러를 걸기로 했고.
- 친구는 있다.에 5달러를 걸었다.
두 사람의 신념은 어떻게 측정가능한가?
- 베팅한 금액의 크기에 비례한 것으로 측정 가능한다.
- P(존재X)/P(존재O) = 100/5 = 20
오즈를 이용한 확률 결정
- P(존재X) = P(존재O) 20 = ( 1 - P(존재X) ) 20
= P(존재X) = 20/21
불확실성의 논리
- AND / OR 관계 설명. (생략)
이항확률분포 생성
- (생략)
베타 분포
베타 분포란?
- 이미 여러번 시행했고, 성공적인 결과의 수의 확률을 구할때 사용
- 예를 들면, 100번 시도해서 40번 성공할 확률
확률 vs 통계, 추론
-
확률 : 사건이 일어날 가능성이 얼마인지 정확히 알고 있음.
-
확률의 관심 분야 : 특정 관찰에 대해 얼마나 가능성 있는지.
-
통계 : 이 문제를 거꾸로 살펴봄.
-
통계의 관심 분야 : 사건들이 발생한 데이터 -> 확률 "추론"
랜덤뽑기 예제.
- 확률을 알 수 없는 랜뽑 기계가 있다.
- 1번 시도했는데 실패했다.
- 이후 40번 추가 시도하여 14번 성공했다.
- 난 처음에 확률이 1/2 일줄 알았다.
- 그런데 아닌 것 같다.
확률의 확률 계산.
- H1 : P(true) = 1/2
- H2 : P(true) = 14/41
- 41번 시도했으므로 H2가 더 그럴듯한 가능성으로 보인다.
- 이를 수학적으로 증명해보자
- 이항분포로 증명해보자.
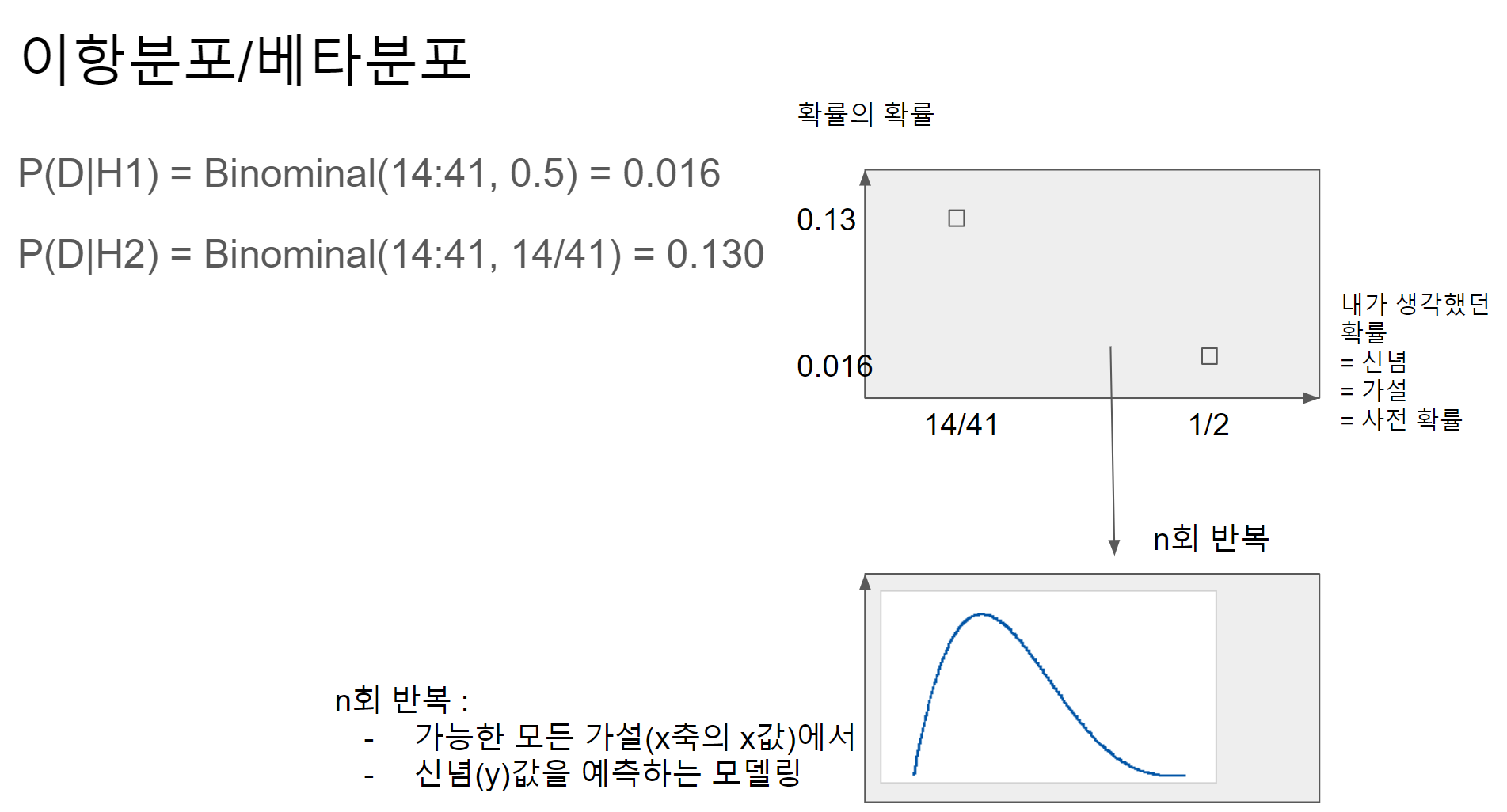
Binominal(14:41,0.5) = 0.5 의 확률로 41회 시도해서 14회 성공할 확률
Binominal(14:41,14/41) = 14/41 의 확률로 41회 시도해서 14회 성공할 확률
y축의 값이 14/41 부분에서 더 높게 나온다.
- y축의 값 : 확률의 확률 : 그럴듯한 가능성
그런데 이산확률분포로 보면 문제점이 2가지 있다.
- (1) : 0.01 간격으로 주어진 p 에서 p가 나올 확률을 구한다고 하면 0.001 간격은? 0.0001 간격은? 그렇다고 무한히 많은 테스트를 할수도 없다.
- (2) : 적당히 높은 신념을 추린다고 했을때, 그래도 값이 너무 많을 수 있고, 이들 값의 합은 1이 되지 않는다.
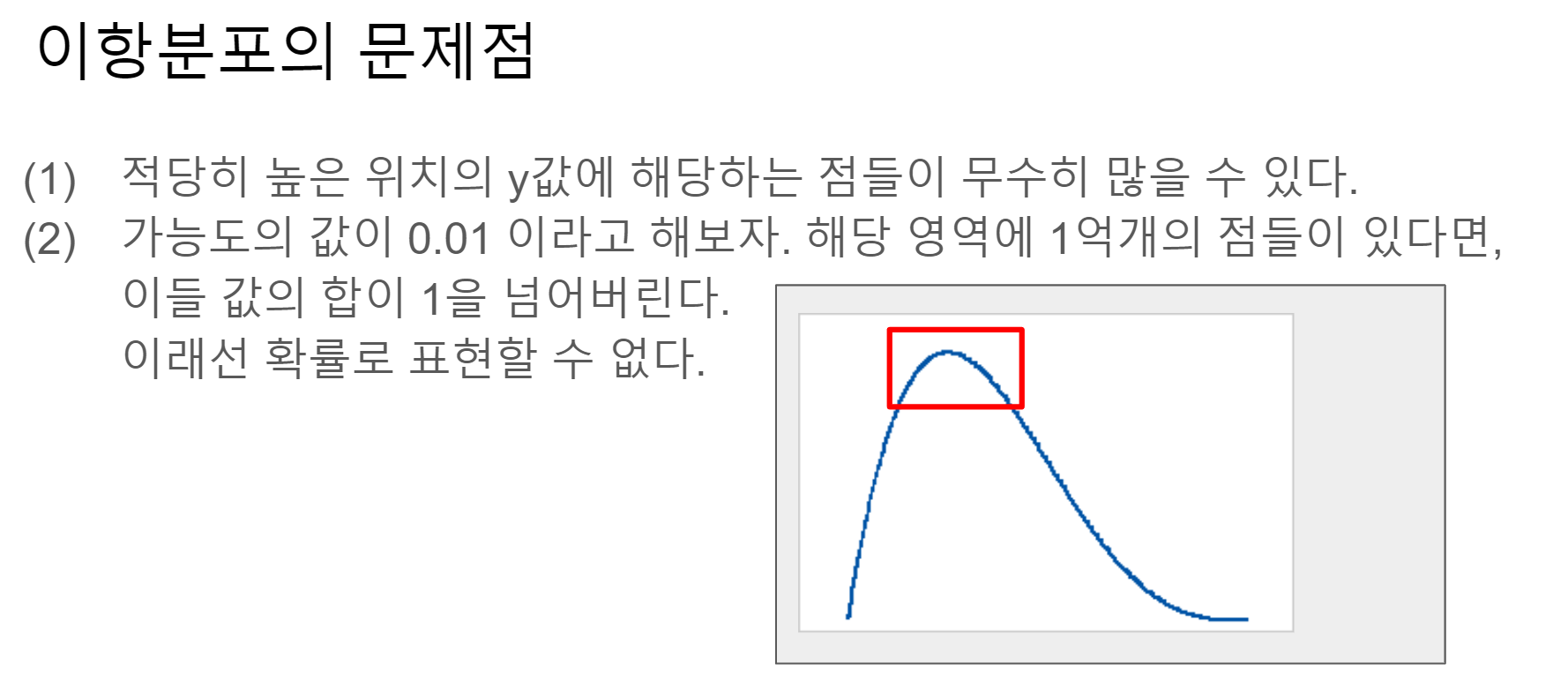
위 문제들로 인해 베타분포를 사용한다.
베타 분포가 생긴 꼴을 보자.
- x : 다양한 가설이다. 후보인 확률들이다.
- alpha : True 인 개수
- beta : False 인 개수 ( 총 시도 횟수 = 알파 + 베타 )
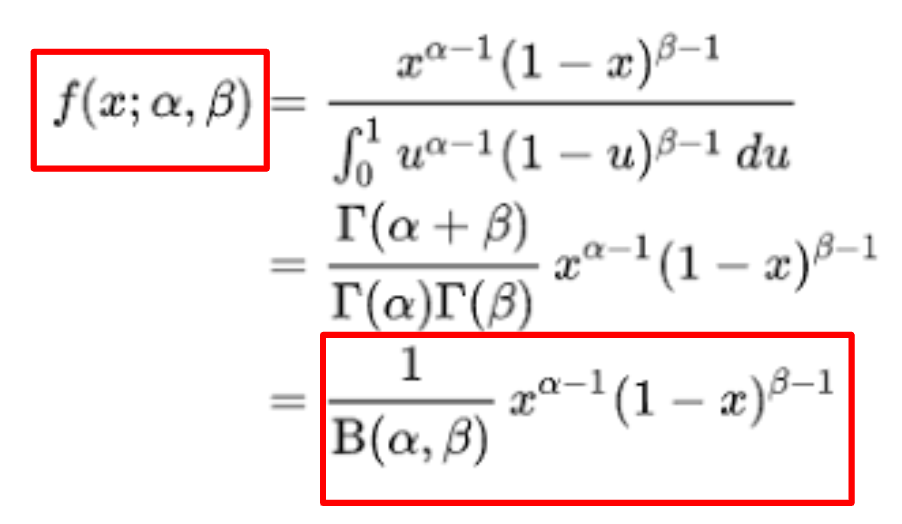
이항 분포에서 달라진 점 :
- 지수 부분에서 1을 빼고, 분모에는 베타 함수가 있어서 나누어진 꼴이다.
- 즉, 정규화를 해준 꼴인데, 이러한 행위는 값의 합계를 1로 만들어줘서 확률의 의미를 갖게하는 의미가 있다.

Quiz
동전을 10번 던져서 4번의 앞면이 나오고 6면이 뒷면이 나왔다. 게임이 공정하다는 가정 하에, 해당 게임이 5% 이내에서 공정할 확률을 구하라.
- 확률이 0.5인 행위를 4번 성공, 6번 실패하는 경우에 대해서 x 값 45%~55% 범위에 해당하는 넓이를 베타분포로 구한다.
- 처음에 나는 로그 오즈비로 구하는 상상을 했었는데 베타분포로도 접근할 수 있구나. 를 느꼈다.
