또할라노비스 ( 업데이트 )

예전부터 궁금증 :

• 마할라노비스 거리를 구하는게 역행렬을 구해야 하기 때문에 실제 문제 적용에 어려운 경우가 있다.
• 마할라노비스 컨셉상 각 축의 선형 변환을 한 다음, 유클리드 거리를 구하는 것으로 어디선가 본 것 같다.
• 그렇다면, 각 축을 std_scale 한 다음, 원점으로부터의 거리를 구하면 되지 않는가?
• 더욱이, robust 한 마할라노비스 거리를 구하고자 한다면 modified z score 변환한 다음, 유클리드 거리를 구하면 되지 않는가?
• 그럼 우선 "각 축을 std_scale 한 다음, 원점으로부터의 거리를 구하면 되지 않는가?" 가 되는지 확인해보자.

df = pd.DataFrame(np.zeros((100,3)), columns=['uniform','gausian','poisson'])
df['uniform'] = np.random.uniform(-100,100,100)
df['uniform_mean'] = df['uniform'].mean()
df['uniform_std'] = df['uniform'].std()

df['gausian'] = np.random.normal(-100,100,100)
df['gausian_mean'] = df['gausian'].mean()
df['gausian_std'] = df['gausian'].std()

df['poisson'] = np.array([pois_dist(n, 2) for n in range(100)])
df['poisson_mean'] = df['poisson'].mean()
df['poisson_std'] = df['poisson'].std()

df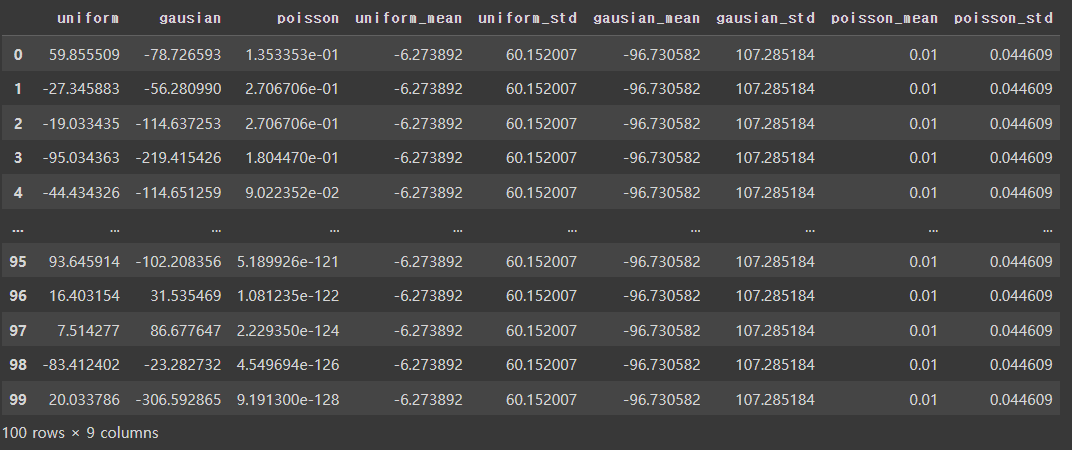

df_std_scaled = df.copy()

df_std_scaled['uniform_z_score'] = df_std_scaled[['uniform','uniform_mean','uniform_std']].apply(lambda x : (x[0]-x[1])/x[2],axis=1)
df_std_scaled['gausian_z_score'] = df_std_scaled[['gausian','gausian_mean','gausian_std']].apply(lambda x : (x[0]-x[1])/x[2],axis=1)
df_std_scaled['poisson_z_score'] = df_std_scaled[['poisson','poisson_mean','poisson_std']].apply(lambda x : (x[0]-x[1])/x[2],axis=1)

df_std_scaled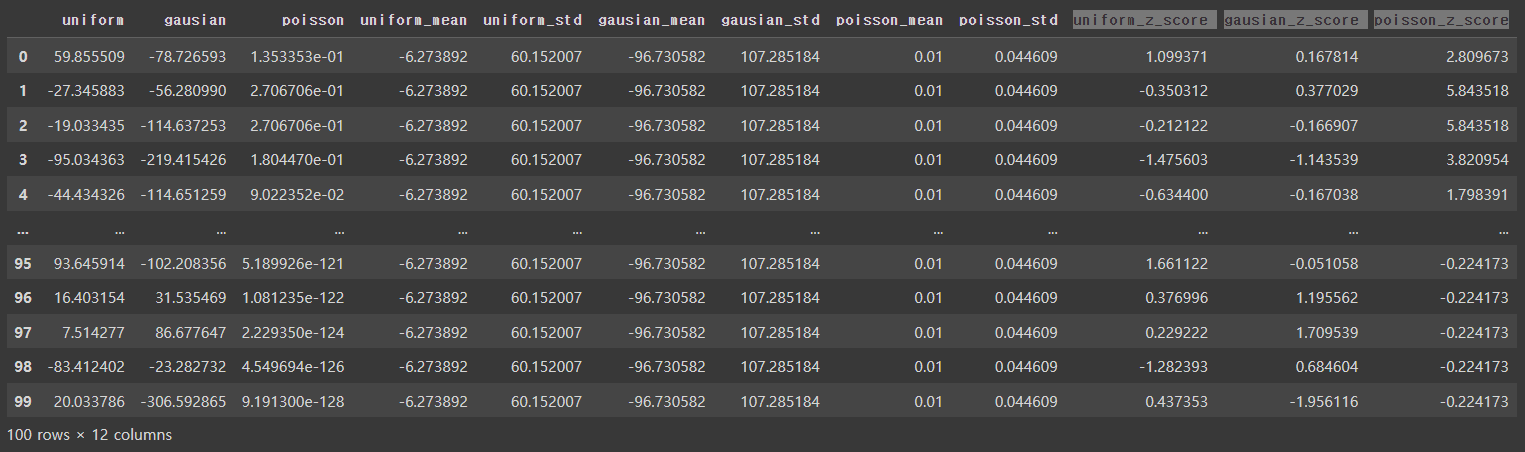

import scipy as sp

def mahalanobis(x=None, data=None, cov=None):
    """Compute the Mahalanobis Distance between each row of x and the data  
    x    : vector or matrix of data with, say, p columns.
    data : ndarray of the distribution from which Mahalanobis distance of each observation of x is to be computed.
    cov  : covariance matrix (p x p) of the distribution. If None, will be computed from data.
    """
    x_minus_mu = x - np.mean(data)
    if not cov:
        cov = np.cov(data.values.T)
    inv_covmat = sp.linalg.inv(cov)
    left_term = np.dot(x_minus_mu, inv_covmat)
    mahal = np.dot(left_term, x_minus_mu.T)
    return mahal.diagonal()

df_mahalanobis = df[['uniform','gausian','poisson']].copy()
df_mahalanobis['mahala'] = mahalanobis(x=df_mahalanobis, data=df[['uniform','gausian','poisson']])
df_mahalanobis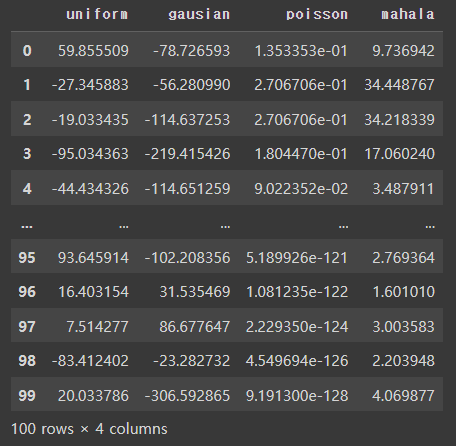

df_mahalanobis_2 = df_std_scaled[['uniform_z_score',	'gausian_z_score',	'poisson_z_score']].copy()

df_mahalanobis_2['mahala'] = df_std_scaled[['uniform_z_score',	'gausian_z_score',	'poisson_z_score']].apply(lambda x : (x[0]**2 + x[1]**2 + x[2]**2) , axis=1)
df_mahalanobis_2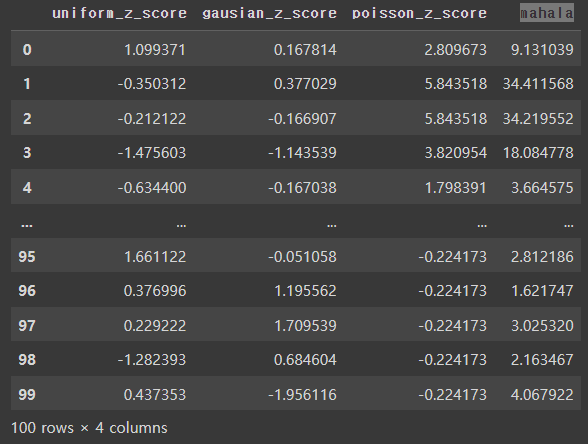

어라? 대충 비슷한거 같다!

시각화를 해보자.

df_mahalanobis['pct_change'].plot(kind='kde')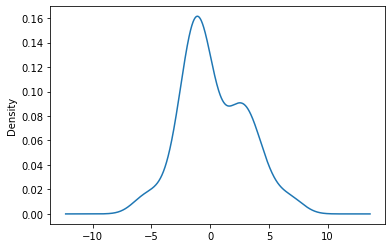

대략 5~10% 정도의 차이만 있을 뿐, 비슷한 값이 나오는 것이 확인된다.

업데이트.

먼저 이 글을 작성하게 된 계기는

• 마할라노비스는 결국 선형변환을 거친 후, 유클리드 거리를 구하는 것이다.

• 그러니 각 축에 대해서 Std Scaling (선형변환) 후 유클리드 거리를 구하면 같은 결과가 나오지 않을까? 했었다.

• 알고보니 그렇지 않다.
  

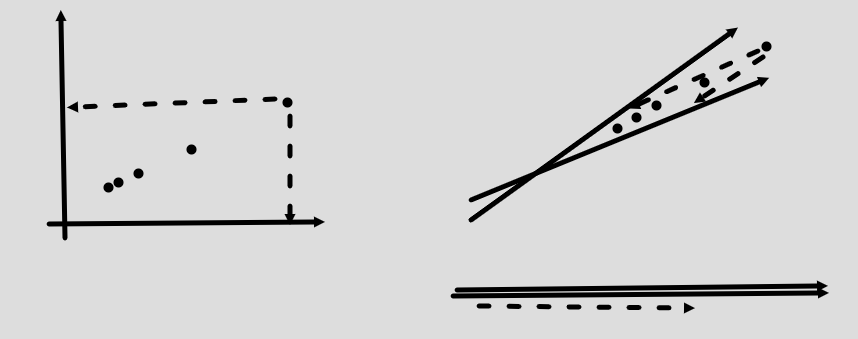
• 직관적으로 생각해보면 두 변수간 상관관계가 매우 높다면 correlation, covariance 둘 다 매우 높을 것이다.

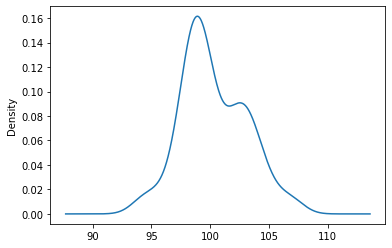
• 그러면 위 그림에서 좌측 1번 그림이 변환 전

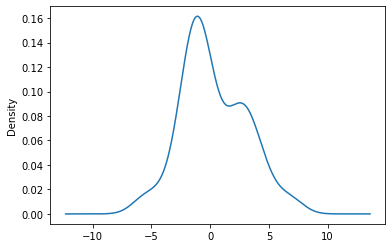
• 우측 2번 그림이 선형 변환 후, 극단적인 케이스

• 좌측에서의 유클리드 거리는 세로 축의 길이가 어느 정도 전체 거리에서 기여하는 바가 있지만

• 우측에서의 유클리드 거리는 세로 축의 길이가 전체 거리에서 기여하는 바가 적음을 알 수 있다.

• 즉, iid 한 경우에만 마할라노비스 거리와 각 축의 stdscaling 후 유클리드 거리가 유사할 것이다.