
알고리즘 문제 풀이 스터디를 하며 만든 자료입니다.
개인 공부 기록용으로 올립니다.
DP(Dynamic Programming)이란?
Dynamic Programming(동적 계획법)은 하나의 큰 문제를 여러 개의 작은 문제로 나누어서, 그 결과를 저장하여 다시 큰 문제를 해결할 때 사용하는 문제해결 패러다임입니다.
❓ 왜 DP가 필요할까?
완전탐색, DFS, BFS로 해결할 수 있지만 경우의 수가 너무 많아 속도가 느려지는 문제들을 효율적으로 해결하기 위해 등장했습니다.
💡 한 교수는 DP를 "기억하기 알고리즘"이라고 번역하기도 했습니다.
DP의 원리와 조건
📌 핵심 원리
- 메모리를 사용해서 중복 연산을 줄이고, 중복 연산을 줄여서 수행 속도를 개선
- 메모리 사용 : 배열 or 자료구조를 만든다.
- 중복 제거 : 연산 결과를 배열에 담는다. 같은 연산을 또 하지 않음
- 재사용: 겹치는 서브 문제는 한 번만 계산하고 결과를 재사용
DP의 사용 조건
-
최적 부분 구조 (Optimal Substructure)
- 큰 문제의 최적해가 작은 문제들의 최적해로 구성됨
-
중복 부분 문제 (Overlapping Subproblems)
- 같은 작은 문제들이 반복적으로 계산됨
DP 사용 시점 판별법
✅ DP를 사용해야 하는 경우
-
DFS/BFS로 풀 수 있지만 경우의 수가 너무 많은 문제
- 일반적으로 DFS/BFS로 처리 가능한 경우의 수: 약 500만개
- 그 이상이면 DP 고려
-
중복적인 연산이 많이 발생하는 경우
- 같은 하위 문제가 여러 번 계산됨
- 최적값을 구하는 과정에서 불필요한 계산 반복
주요 문제 유형
- 최적화 문제: 최대값, 최소값을 구하는 문제
- 경우의 수: 가능한 방법의 수를 구하는 문제
- 경로 탐색: 최단 경로, 최적 경로 문제
예시: 가장 빨리 도착하는 경로의 소요 시간, 주식 매매 최적 타이밍
💡 DP 문제 해결의 핵심 질문
"어떻게 해야 뒤로 돌아가지 않을 수 있을까?"
구현 방식 : Top-Down vs Bottom-Up

| Top-Down | Bottom-Up | |
|---|---|---|
| 구조 | recursive(재귀) | iterative(반복문) |
| subproblem 결과 저장 | memoization | tabulation |
| 선호하는 경우 | subproblem의 일부만 계산해도 최종 솔루션을 구할 수 있을 때 | 모든 subproblem을 계산해야 최종 솔루션을 구할 수 있을때 |
⬇️ Top-Down (Memoization)
큰 문제를 해결하기 위해, 재귀적으로 작은 문제를 호출하며 해결
- dp[n] 같은 목표상태에서 출발
- 필요한 하위 문제를 재귀적으로 호출
- 이미 계산된 값은 메모리에 저장되 있던 내역 꺼내서 활용해 중복 계산 방지
→ 큰 문제에서 작은 문제로(top-down) 내려가며 해결하는 방식
⚠️ 주의사항: 함수 호출이 많아지면 호출 오버헤드, 스택 오버플로우 위험 있음
⬆️ Bottom-Up (Tabulation)
작은 규모의 문제부터 시작해 전체 큰 문제를 해결
- dp[0] 같은 베이스부터 출발
- 반복문을 사용해 테이블을 채워나가는(table-filling) 방식
- 모든*하위 문제를 반복문으로 순차적으로 해결하면서 결과를 테이블에 저장해 중복 계산을 방지
→ 작은 문제를 해결하면서 점점 위로(bottom-up) 올라가는 방식 (주로 사용)
💡 장점: 스택 오버플로우 걱정 없음, 경우에 따라 공간 최적화 가능
ex. 직전 값만 사용하는 경우 리스트가 아닌 변수 사용
근본적인 개념으로 "결과값을 기억하고 재활용" 한다는 측면에서는 Memoization, Tabulation이 크게 다르지 않음
실전 문제 해결 예시
Top-Down 예시: Climbing Stairs
Leetcode - Climbing Stairs
정상까지 오르는데 N번의 스텝이 필요한 계단에서 한번에 한 스텝 혹은 두 스텝을 오를 수 있을때 정상까지 올라가는 방법의 수는?
문제 분석
- 한번에 한스텝 혹은 두 스텝을 오를 수 있음
- n = 6일때,이전 계단은 5층 or 4층
→ 해당 값에서 시작해 계속 아래로 내려간다. - 점화식:
climb(n) = climb(n-1) + climb(n-2)
Step 1: 일반 재귀 (비효율적)
// 시간복잡도: O(2^n) - 매우 비효율적!
function climb(n){
if(n<=2) return n;
return climb(n-1) + climb(n-2)
}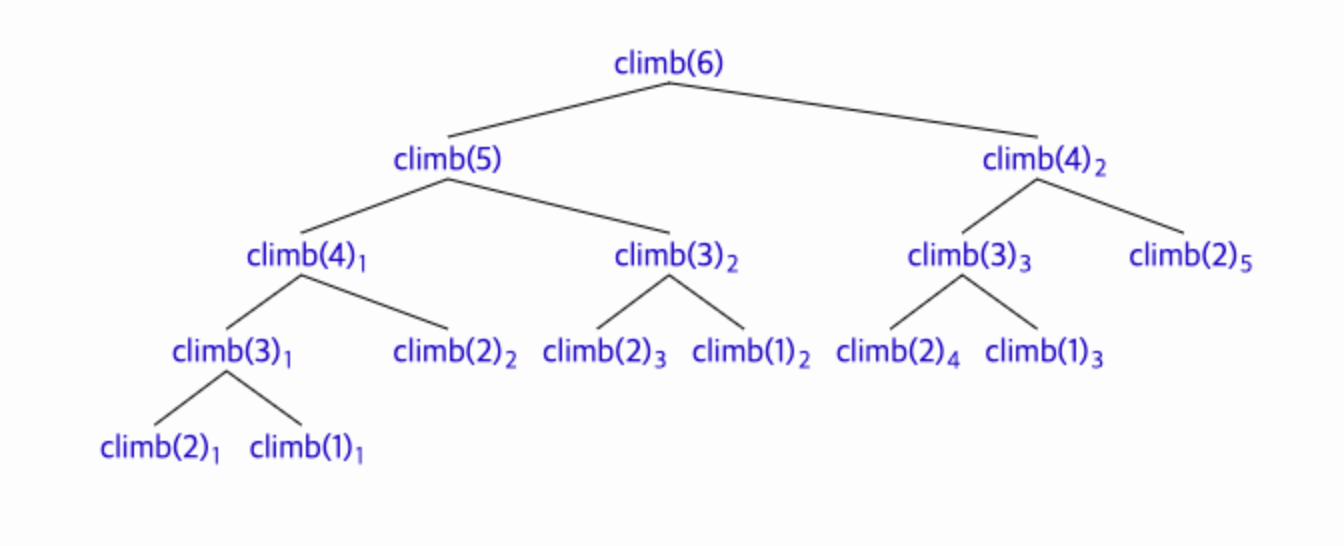
문제점 : 동일한 input에 대한 function call이 많은 것을 확인 할 수 있음
→ 메모해 뒀다가 이후 재사용하는 방식으로 변경
Step 2: Top-Down DP (Memoization)
// 시간복잡도: O(n)
let memo = [];
function climb(n){
if(n<=2) return n;
// 이미 계산된 값이 있으면 바로 반환
if (memo[n] !== undefined)
return memo[n];
// 없으면 계산 후 저장
memo[n] = climb(n-1) + climb(n-2);
return memo[n]
}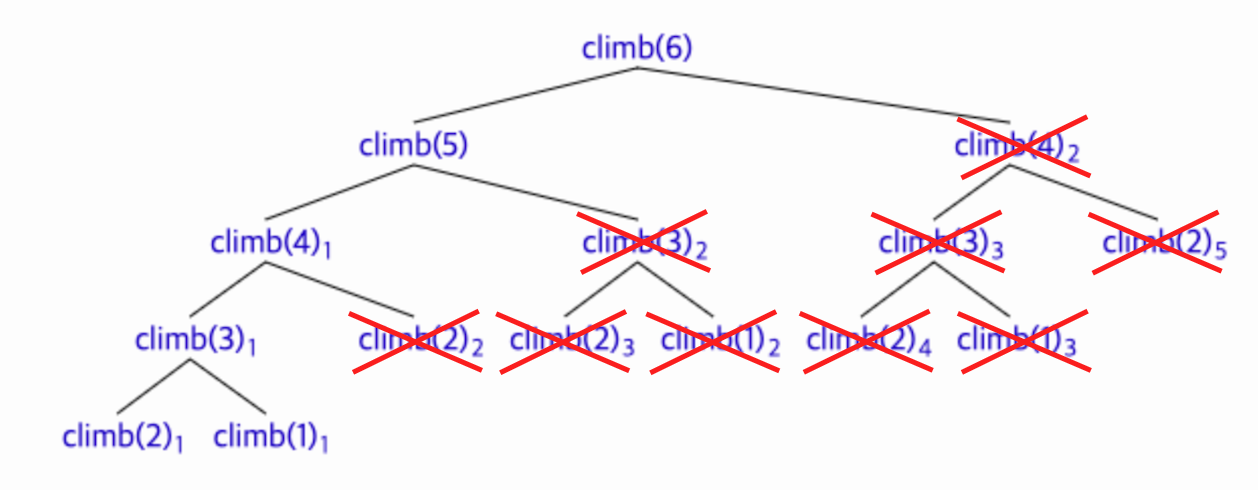
Top-Down of DP
- recursive(재귀)
- memoization(메모리에 저장)
- funcatioin call의 결과를 저장해서 이후에 같은 input에 대한 호출은 저장한 결과를 사용하는 것
Bottom-Up 예시: 연속합
백준 - 연속합
n개 정수 수열에서 연속된 몇 개의 수를 선택해서 구할 수 있는 합 중 가장 큰 값은?
예시: [10, -4, 3, 1, 5, 6, -35, 12, 21, -1] -> 33(12+21)
문제 분석
arr[i] 까지 왔을때, 최대인 연속 합이 나오는 2가지
1. arr[i] 자체만 선택
2. 이전까지의 최대 연속합에 arr[i] 를 더하는 경우
- 점화식:
dp[i] = Math.max(arr[i], dp[i-1] + arr[i])
Step 1: 기본 DP 구현
// 시간복잡도: O(n), 공간복잡도: O(n)
function solution(N, arr) {
const dp = Array(N).fill(0);
dp[0] = arr[0];
let maxSum = dp[0];
for (let i = 1; i < N; i++) {
dp[i] = Math.max(arr[i], dp[i - 1] + arr[i]);
maxSum = Math.max(maxSum, dp[i]);
}
return maxSum;
}
잘 보면 결국 바로 직전의 값만 사용하는 것을 확인할 수 있음
→ 꼭 배열 형태로 사용할 필요가 없다!
Step 2: 메모리 ㅊ최적화
dp 배열 없이 현재 상태만 저장해서 메모리 사용을 줄임
// 시간복잡도: O(n), 공간복잡도: O(1)
function solution2(N, arr) {
let current = arr[0];
let maxSum = arr[0];
for (let i = 1; i < N; i++) {
current = Math.max(arr[i], current + arr[i]);
maxSum = Math.max(maxSum, current);
}
return maxSum;
}
실제 활용 사례
- Google Maps의 경로 탐색
: 다양한 경로 중에서 최단 경로를 순차적으로 찾는 데 활용 - 네트워크 데이터 전송
: 송신자에서 여러 수신자에게 데이터를 순차적으로 전송할 때 최적화된 경로를 찾는 데 사용 - 문서 유사도 분석
: Google, Wikipedia, Quora 등의 검색 엔진에서 두 텍스트 문서 간의 유사성 정도를 측정하는 알고리즘에 활용 - 맞춤법 검사
: 편집 거리(Edit Distance) 알고리즘을 사용하여 오타를 찾고 올바른 단어를 제안하는 맞춤법 검사기에서 활용 - 데이터베이스 캐싱 시스템
- Git 병합 (Git Merge)
: 문서 비교에서 최장 공통 부분수열(LCS) 알고리즘을 사용하는 대표적인 사례 - 유전 알고리즘
: 최적화 문제를 해결하는 유전 알고리즘의 핵심 연산에 활용