116. Populating Next Right Pointers in Each Node
문제
완전이진트리가 주어진다. 각 노드의 next 포인터에 같은 레벨에 있는 우측 노드를 연결해라.(가장 오른쪽 노드의 next 는 NULL)

Input: root = [1,2,3,4,5,6,7]
Output: [1,#,2,3,#,4,5,6,7,#]
Explanation: Given the above perfect binary tree (Figure A), your function should
populate each next pointer to point to its next right node, just like in Figure B.
The serialized output is in level order as connected by the next pointers,
with '#' signifying the end of each level.해결
기본적으로 tree를 BFS순회. 단 right, left 자식 순서로 queue에 넣는다. 그리고 level이 바뀌면 null부터 시작해서 순차적으로 노드를 등록. 아래 BFS코드는 템플릿처럼 외울것!
class Solution {
public:
Node* connect(Node* root) {
if (!root)
return root;
queue<pair<Node *, int>> q;
Node *prev = NULL;
int prev_level = 0;
root->next = NULL;
q.push(make_pair(root, 0));
while (!q.empty()) {
pair<Node *, int> check = q.front();
q.pop();
Node *node = check.first;
int level = check.second;
if (prev_level != level) {
prev = NULL;
prev_level = level;
}
node->next = prev;
prev = node;
if (node->right)
q.push(make_pair(node->right, level + 1));
if (node->left)
q.push(make_pair(node->left, level + 1));
}
return root;
}
};103. Binary Tree Zigzag Level Order Traversal
문제
주어진 트리를 각 레벨별로 출력하되, 순서를 매 레벨마다 바꿔라.
가령 아래 예에서 3(->방향) 을 출력, 그 다음레벨은 20 9(<-방향), 그 뒤는 15 7 (->방향)

Input: root = [3,9,20,null,null,15,7]
Output: [[3],[20,9],[15,7]]해결
class Solution {
public:
vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
vector<vector<int>> ret;
if (!root)
return ret;
vector<int> cur_lv;
queue<pair<TreeNode *, int>> q;
int prev_level = 0;
int level = 0;
q.push(make_pair(root, 0)); //val, level
while (!q.empty()) {
pair<TreeNode *, int> check = q.front();
q.pop();
TreeNode *cur_node = check.first;
level = check.second;
if (prev_level != level) { // when next level begin, push prev level vector
if (level % 2 == 0)
std::reverse(cur_lv.begin(), cur_lv.end());
ret.push_back(cur_lv);
cur_lv.clear();
}
cur_lv.push_back(cur_node->val);
prev_level = level;
if (cur_node->left)
q.push(make_pair(cur_node->left, level + 1));
if (cur_node->right)
q.push(make_pair(cur_node->right, level + 1));
}
if (level % 2 != 0)
std::reverse(cur_lv.begin(), cur_lv.end());
ret.push_back(cur_lv);
return ret;
}
};542. 01 Matrix
문제
각각의 셀마다 가장 가까운 0의 거리는?
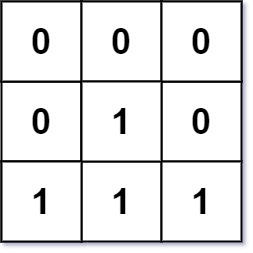
Input: mat = [[0,0,0],[0,1,0],[1,1,1]]
Output: [[0,0,0],[0,1,0],[1,2,1]]아이디어
- Idea
- brute-force search mat from 0 to n -> O(N^2) (N=m*n)
- using Queue -> O(N) / O(N)
문제를 보면 0주변은 1, 1주변은 2 이런식으로 증가된다. 너비우선으로 값이 증가되는 구조다. 즉 일종의 BFS형태. 이런 형태는 Queue를 사용하는게 국률이다. 기억하기!! - possible O(N) / O(1)? -
해결 O(N)/ O(N) (N=m*n)
- 먼저 0인 좌표를 queue에 push
- pop 하고 주변값이 1이면 pop한 값에 + 1한값을 더함, 그 좌표는 push
- 한번 queue에 push했던 좌표는 visited체크,
- 이것을 반복한다.
class Solution {
std::queue<pair<int, int>> q;
int rsize;
int csize;
vector<vector<int>> visit; // 수행속도는 함수 매개변수로 넘기는 방식이 더 빨랐음.
void inc_count_push(vector<vector<int>> &mat, int r, int c) {
int pos_val = mat[r][c];
// check 4 direction from pop position
// if on 4 each value is 1 -> increase by pos_val + 1
// then push it
if (r-1 >= 0 && visit[r-1][c] == 0 && mat[r-1][c] == 1) {
mat[r-1][c] = pos_val + 1;
q.push(make_pair(r-1, c));
visit[r-1][c] = 1;
}
if (r+1 < rsize && visit[r+1][c] == 0 && mat[r+1][c] == 1) {
mat[r+1][c] = pos_val + 1;
q.push(make_pair(r+1, c));
visit[r+1][c] = 1;
}
if (c-1 >= 0 && visit[r][c-1] == 0 && mat[r][c-1] == 1) {
mat[r][c-1] = pos_val + 1;
q.push(make_pair(r, c-1));
visit[r][c-1] = 1;
}
if (c+1 < csize && visit[r][c+1] == 0 && mat[r][c+1] == 1) {
mat[r][c+1] = pos_val + 1;
q.push(make_pair(r, c+1));
visit[r][c+1] = 1;
}
}
public:
vector<vector<int>> updateMatrix(vector<vector<int>>& mat) {
rsize = mat.size();
csize = mat[0].size();
//vector<vector<int>> visit(rsize, vector<int> (csize, 0));
visit = vector<vector<int>> (rsize, vector<int> (csize, 0));
for (int i = 0; i < rsize; i++) {
for (int j = 0; j < csize; j++) {
if (mat[i][j] == 0)
q.push(make_pair(i, j));
}
}
while (!q.empty()) {
pair<int, int> pos = q.front();
q.pop();
inc_count_push(mat, pos.first, pos.second);
}
return mat;
}
};2차원 vector 초기화 방법
숙지하자.
vector<vector<int>> visit(rsize, vector<int> (csize, 0)); - 전역변수 선언, 초기화는 로컬에서
vector<vector<int>> visit; //전역 선언
visit = vector<vector<int>> (rsize, vector<int> (csize, 0)); //초기화994. Rotting Oranges
문제
주어진 오렌지 상자에 썪은오렌지(2), 정상오렌지(1) 없음(0) 이 존재한다. 썪은 오렌지는 한번에 상하좌우 4방향을 오염시킨다. 몇 번만에 모든 오렌지가 썪는지 파악해라.

Input: grid = [[2,1,1],[1,1,0],[0,1,1]]
Output: 4참고로 썪은 오렌지가 두개 이상일 수있음.
Input: grid = [[2,1,1],[1,1,2],[0,1,1]]
Output: 2해결 BFS
처음에 재귀로 풀려고시도했지만 잘 안풀렸음. queue사용해 pop할때 상하좌우 위치를 체크해서 push하면됨. queue를 이용해 그래프의 bfs 순회 하는것과 구조상 동일
class Solution {
int r_size;
int c_size;
bool is_fresh(vector<vector<int>>& grid, int r, int c) {
if (r < 0 || r >= r_size || c < 0 || c >= c_size)
return false;
if (grid[r][c] == 1)
return true;
return false;
}
void rotting(queue<tuple<int, int, int>> &q, vector<vector<int>> &grid, int r, int c, int step) {
if (is_fresh(grid, r, c)) {
grid[r][c] = 2;
q.push(make_tuple(r, c, step + 1));
}
}
public:
int orangesRotting(vector<vector<int>>& grid) {
r_size = grid.size();
c_size = grid[0].size();
queue<tuple<int, int, int>> q; // (row, col, step)
int r = 0;
int c = 0;
int step = 0;
for (int i = 0; i < r_size; i++) {
for (int j = 0; j < c_size; j++) {
if (grid[i][j] == 2)
q.push(make_tuple(i, j, 0));
}
}
while (!q.empty()) {
tuple<int, int, int> check = q.front();
q.pop();
r = get<0>(check);
c = get<1>(check);
step = get<2>(check);
rotting(q, grid, r+1, c, step);
rotting(q, grid, r, c+1, step);
rotting(q, grid, r-1, c, step);
rotting(q, grid, r, c-1, step);
}
for (int i = 0; i < r_size; i++) {
for (int j = 0; j < c_size; j++) {
if (grid[i][j] == 1) {
step = -1;
break;
}
}
}
return step;
}
};199. Binary Tree Right Side View
문제
주어진 트리를 우측에서 바라볼때 노드 값을 리턴하라.

해결
BFS로 순회. root부터 queue에 넣고, pop하면서 처음으로 height가 커질때마다 값들을 ret Vector에 저장. 아주 흥미로운 문제 였다.
class Solution {
public:
vector<int> rightSideView(TreeNode* root) {
vector<int> ret;
queue<pair<TreeNode *, int>> q;
int cur_h = 0;
if (root)
q.push(make_pair(root, cur_h + 1));
while (!q.empty()) {
pair<TreeNode *, int> check = q.front();
q.pop();
TreeNode *node = check.first;
if (check.second > cur_h) {
ret.push_back(node->val);
cur_h = check.second;
}
if (node->right)
q.push(make_pair(node->right, cur_h + 1));
if (node->left)
q.push(make_pair(node->left, cur_h + 1));
}
return ret;
}
};102. Binary Tree Level Order Traversal
문제
트리를 순회하는데 동일한 level에 있는 노드끼리 분류해서 값을 리턴하라. 아래 output참고.

Input: root = [3,9,20,null,null,15,7]
Output: [[3],[9,20],[15,7]]해결 (DFS)
dfs 순회 하면서 2차원 벡터의 level 인덱스에 값을 push_back()한다. 문제는 level인덱스가 없을때인데, 그 조건은 ret.size()가 level과 같거나 작다면 아직 level인덱스에 값이 없다는 뜻이다. 그 조건일때만 첫 벡터를 생성해서 push_back() 한다.
class Solution {
void level_order_travel(TreeNode *root, int level, vector<vector<int>> &ret) {
if (root == NULL)
return;
if (ret.size() <= level) { /* there is no ret[level], need to addsign a new vector */
vector<int> lv;
lv.push_back(root->val);
ret.push_back(lv);
} else {
ret[level].push_back(root->val);
}
level_order_travel(root->left, level + 1, ret);
level_order_travel(root->right, level + 1, ret);
}
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> ret;
level_order_travel(root, 0, ret);
return ret;
}
};해결 (BFS)
BFS순회를 하면서, 현재 높이를 기록해뒀다가 증가하면 저장.
https://velog.io/@soopsaram/Leetcode-199.-Binary-Tree-Right-Side-View 풀이와 동일하게 BFS순회 함.
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> ret;
if (root == NULL)
return ret;
vector<int> tmp;
queue<pair<TreeNode *, int>> q;
int prev_height = 0;
if (root)
q.push(make_pair(root, prev_height + 1));
while (!q.empty()) {
pair<TreeNode *, int> check = q.front();
q.pop();
TreeNode *node = check.first;
int cur_h = check.second;
if (cur_h == prev_height + 2) { // insert tmp to ret
ret.push_back(tmp);
prev_height++;
tmp.clear();
}
if (cur_h == prev_height + 1) { // make tmp (current height's vector)
tmp.push_back(node->val);
}
if (node->left) q.push(make_pair(node->left, cur_h + 1));
if (node->right) q.push(make_pair(node->right, cur_h + 1));
}
ret.push_back(tmp); // insert the last tmp
return ret;
}
};
