Discuss 중에 추천 글 -> How to approach most of DP problems.
DP문제 풀이의 정석임. 반드시 또 읽기!
This particular problem and most of others can be approached using the following sequence:
Find recursive relation
Recursive (top-down)
Recursive + memo (top-down)
Iterative + memo (bottom-up)
Iterative + N variables (bottom-up)if a problem is asking for the maximum/minimum/longest/shortest of something, the number of ways to do something, or if it is possible to reach a certain point, it is probably greedy or DP.
416. Partition Equal Subset Sum
문제
주어진 배열을 두개의 subset으로 나누었을때, 두 subset의 합이 같은 경우가 존재하는지 판단하라.
가령 아래 예의 경우 [1, 5, 5] 와 [11] 두개의 subset의 합이 동일해서 true이다.
Input: nums = [1,5,11,5]
Output: true
Input: nums = [1,2,3,5]
Output: false아이디어
- 처음에 시도했던건 backtracking으로 1 ~ n개를 선택하는 모든 경우의수를 탐색하는거였음. 너무 비효율적 당연히 TLE
- DP방법은 해설을 조금 참고, 재귀적 관계 아이디어를 얻음.
- 마지막 인덱스 값부터 해당 인덱스를 선택하거나 안하거나 이 두가지 경우의 재귀호출을 하면된다.
f(i, sum) = f(i - 1, sum - nums[i]) or f(i - 1, sum) - 이런 형식의 재귀호출은 익숙치 않았다. 잘 기억하기!
해결 - brute force (TLE)
class Solution {
bool dfs(vector<int> nums, int idx, int sum) {
if (sum == 0)
return true;
if (idx < 0 || sum < 0)
return false;
return dfs(nums, idx - 1, sum - nums[idx]) || dfs(nums, idx - 1, sum);
}
public:
bool canPartition(vector<int>& nums) {
int tot_sum = 0;
for (auto it: nums)
tot_sum += it;
if (tot_sum % 2 == 0)
tot_sum /= 2;
else
return false;
return dfs(nums, nums.size() - 1, tot_sum);
}
};해결 DP top-down (memoization)
DFS with memoization
class Solution {
vector<vector<int>> mem;
bool dfs(vector<vector<int>> &mem, vector<int> nums, int idx, int sum) {
if (sum == 0)
return true;
if (idx < 0 || sum < 0)
return false;
if (mem[idx][sum] != -1)
return mem[idx][sum];
mem[idx][sum] = dfs(mem, nums, idx - 1, sum - nums[idx]) || dfs(mem, nums, idx - 1, sum);
return mem[idx][sum];
}
public:
bool canPartition(vector<int>& nums) {
int tot_sum = 0;
for (auto it: nums)
tot_sum += it;
if (tot_sum % 2 == 0)
tot_sum /= 2;
else
return false;
mem = vector<vector<int>>(nums.size() + 1, vector<int>(tot_sum + 1, -1));
return dfs(mem, nums, nums.size() - 1, tot_sum);
}
};279. Perfect Squares
문제
어떤 수를 1, 4, 9, 16과 같은 완전제곱수(Perfect Square)의 합으로 나타낼수 있을때, 해당 수를 표현할 수 있는 최소한의 완전제곱수의 갯수는 몇개 인가?
Input: n = 12
Output: 3
Explanation: 12 = 4 + 4 + 4.
Input: n = 13
Output: 2
Explanation: 13 = 4 + 9.해결 아이디어
f(n) = min(f(n - 1^2), ~ , f(n - i^2)) + 1 이라는 점화식 관계를 구할 수 있음. 단 i 는 i*i <= n 까지
해결
backtracking + memoization으로 해결
class Solution {
int mem[10001];
public:
int numSquares(int n) {
int ret = INT_MAX;
if (mem[n])
return mem[n];
if (n == 0)
return 0;
for (int i = 1; i*i <= n; i++) {
if (n - (i*i) < 0)
continue;
ret = min(ret, numSquares(n - (i*i)) + 1);
}
mem[n] = ret;
return ret;
}
};91. Decode Ways
문제
숫자로 이루어진 문자열이 주어진다. 각 수들이 문자로 decode된다면 총 몇가지 경우의 수 가 존재하는가?
"AAJF" with the grouping (1 1 10 6)
"KJF" with the grouping (11 10 6)'A' -> "1"
'B' -> "2"
...
'Z' -> "26"Input: s = "226"
Output: 3
Explanation: "226" could be decoded as "BZ" (2 26), "VF" (22 6), or "BBF" (2 2 6).해결
f(n) = f(n + 1) + f(n + 2) 라는 재귀적인 구조는 쉽게 파악할수 있었는데, base case 종료조건을 자꾸 틀려서 애먹음.
추가로 memoization 을 안하면 TLE 발생.
class Solution {
unordered_map<string, bool> map;
unordered_map<int, int> mem;
int recur(string s, int cur) {
if (mem.find(cur) != mem.end())
return mem[cur];
if (cur == s.length()) // <- 종료조건 마지막 바로 다음 index에 도달했다면 decode에 성공했다는 뜻.
return 1;
if (cur > s.length() || s[cur] == '0')
return 0;
int ret = 0;
if (map.find(s.substr(cur, 1)) != map.end())
ret += recur(s, cur + 1);
if (map.find(s.substr(cur, 2)) != map.end())
ret += recur(s, cur + 2);
mem[cur] = ret;
return ret;
}
public:
int numDecodings(string s) {
for (int i = 1; i <= 26; i++)
map[std::to_string(i)] = true;
return recur(s, 0);
}
};아래는 221016 다시 풀어본 더 효율적 풀이, memoization용으로만 해시테이블이 추가로 필요.
class Solution {
public:
unordered_map<int, int> mem;
/* f(i) = f(i+1) + f(i+2) */
int recur(string s, int cur) {
if (mem.find(cur) != mem.end())
return mem[cur];
if (cur == s.length())
return 1;
if (cur > s.length() || s[cur] == '0')
return 0;
int ret = recur(s, cur + 1);
if (stoi(s.substr(cur, 2)) <= 26)
ret += recur(s, cur + 2);
mem[cur] = ret;
return ret;
}
int numDecodings(string s) {
return recur(s, 0);
}
};55. Jump Game
문제
다음 인덱스로 점프할수 있는 최대 거리가 기록된 배열이 주어진다. [0] 부터 점프를 시작한다고 할때, 마지막 인덱스에 도달할 수 있는지 없는지 판단하라.
Input: nums = [2,3,1,1,4]
Output: true
Explanation: Jump 1 step from index 0 to 1, then 3 steps to the last index.
Input: nums = [3,2,1,0,4]
Output: false
Explanation: You will always arrive at index 3 no matter what. Its maximum jump length is 0, which makes it impossible to reach the last index.아이디어
- O(n^2)
맨마지막-1 부터 [0] 까지 앞으로 하나씩 파악한다. 그리고 현재 인덱스에서 갈수 있는 최대 거리까지 모두 탐색한다. 그리고 mem[] 배열에 따로 저장하고 true가 있는지 체크. 최악의경우 O(n^2)의 시간복잡도를 갖고 O(n)의 공간복잡도를 갖는다.
2 4 2 1 0 4 0 0 0 3
T T F F F T F F F- O(n) DP + memoiazation
f(i) = f(i+1) ~ f(i+num[i]) 중에 true가 있으면 true리턴. (back tracking 기반)
재귀적으로 반복하고 이미 풀었던 계산은 메모이제이션하기.
해결 O(n^2)
class Solution {
public:
bool canJump(vector<int>& nums) {
int nsize = nums.size();
if (nsize == 1) return true;
vector<bool> mem(nsize, false);
for (int i = nsize - 2; i >= 0; i--) {
for (int j = i; j <= i + nums[i]; j++) {
if (j == nsize - 1 || mem[j] == true) {
mem[i] = true;
if (i == 0)
return true;
break;
}
}
}
return false;
}
};해결 DP O(n)
드라마틱하게 빨라지지는 않았음.
class Solution {
vector<int> mem;
int last_idx;
bool check_reach(vector<int>& nums, int cur, int end) {
if (mem[cur] != -1)
return mem[cur];
if (cur == last_idx)
return true;
if (end > last_idx)
end = last_idx;
for (int i = cur + 1; i <= end; i++) {
if (mem[i] == -1)
mem[i] = check_reach(nums, i, i + nums[i]);
if (mem[i] == true)
return true;
}
mem[cur] = false;
return mem[cur];
}
public:
bool canJump(vector<int>& nums) {
last_idx = nums.size() - 1;
if (last_idx == 0) return true;
mem = vector<int>(nums.size(), -1);
return check_reach(nums, 0, nums[0]);
}
};45. Jump Game II
문제
각 인덱스에서 최대 점프거리를 나타낸 배열이 주어진다. 0인덱스에서 시작해서 마지막 인덱스에 도달할 수 있는 최소 점프횟수는?
Input: nums = [2,3,1,1,4]
Output: 2
Explanation: The minimum number of jumps to reach the last index is 2. Jump 1 step from index 0 to 1, then 3 steps to the last index.해결 DP
f(0) = min(f(1) ~ f(1+num[0])) 와 같은 점화식으로 재귀+memoization으로 풀기.
class Solution {
int last_idx;
vector<int> mem;
vector<int> nums;
int min_jump(int cur) {
if (cur == last_idx)
return 0;
int local_min = 20000;
int until_idx = std::min(last_idx, cur + nums[cur]);
for (int i = cur + 1; i <= until_idx; i++) {
if (mem[i] == -1) // call recursion
local_min = std::min(local_min, min_jump(i) + 1);
else // get memoization
local_min = std::min(local_min, mem[i] + 1);
}
mem[cur] = local_min;
return local_min;
}
public:
int jump(vector<int>& orig) {
last_idx = orig.size() - 1;
mem = vector<int>(orig.size(), -1);
nums = orig;
return min_jump(0);
}
};해결 gready O(n)
솔루션 참고. 풀이 다시 살펴볼것.
#define max(a, b) (((a) > (b)) ? (a) : (b))
int jump(int* nums, int numsSize){
int maxidx = 0;
int curjumpend= 0;
int cnt = 0;
for (int i = 0; i < numsSize - 1; i++) {
maxidx = max(maxidx, i + nums[i]);
if (i == curjumpend) {
cnt++;
curjumpend = maxidx;
}
}
return cnt;
}1155. Number of Dice Rolls With Target Sum
문제
k개의 면을 가진 주사위 n개가 존재한다. 이 주사위 n개를 던졌을때, 그 합이 target값이 나오는 경우의 수를 구하라. 결과 값은 % 1000000007 으로 모듈러 연산해서 리턴하라(오버플로우 발생예방)
Input: n = 2, k = 6, target = 7
Output: 6
Explanation: You throw two dice, each with 6 faces.
There are 6 ways to get a sum of 7: 1+6, 2+5, 3+4, 4+3, 5+2, 6+1.각각의 주사위 값은 유니크하다. (1,6) (6,1)은 독립적인 경우의 수다.
Back Tracking (Brute-force 방법)
먼저 생각해 볼 수 있는 방법은, Back Tracking으로 완전탐색 하는것이다. n을 하나씩 줄이면서 다음 재귀함수를 호추하고 인자로 현재 sum을 넘긴다. 그리고 sum==target일때, 1을 리턴한다. 결과는 TLE가 발생한다.
// n: number of k-faces dice
class Solution {
vector<vector<int>> memo;
int total;
int bt(int n, int face, int sum, int tgt) {
/* base case */
if (n == 0) {
if (sum == tgt) //found
return 1;
return 0;
}
int way = 0;
for (int i = 1; i <= face; i++) {
way = (way + bt(n - 1, face, sum + i, tgt)) % 1000000007;
}
return way;
}
public:
int numRollsToTarget(int n, int k, int target) {
memo = vector<vector<int>>(n + 1, vector<int>(target + 1, -1));
return bt(n, k, 0, target);
}
};
해결 DP (top-down with memoization)
[주사위 번호] 현재까지 합 이라고 해보자. 예시로 n:3 k:3 target:7이 주어진다. 이를 그림으로 풀어가보면 아래와 같이 (주사위번호, 현재까지 합) 에 따른 중복된 재귀호출을 발견할 수 있다. 따라서 이부분은 memoization을 한다.
[0]1 ...
+1 +2 +3
[1]2 [1]3 [1]4
+1 +2 +3
[2]3 [2]4 [2]5 [2]4 [2]5 [2]6 ...
^^^ ^^^ ^^^ ^^^ 중복된 호출들위의 Back Tracking 구조에서 memo[] 처리 부분만 추가한다.
// n: number of k-faces dice
class Solution {
vector<vector<int>> memo;
int total;
int bt(int n, int face, int sum, int tgt) {
/* base case */
if (sum > tgt) // sum이 memo[]배열을 초과할경우 에러 예방
return 0;
if (n == 0) {
if (sum == tgt) //found
return 1;
return 0;
}
if (memo[n][sum] != -1)
return memo[n][sum];
int way = 0;
for (int i = 1; i <= face; i++) {
// bt() with unique (n, sum) is calculated repeatedly. and it return the same result, so memoize it.
way = (way + bt(n - 1, face, sum + i, tgt)) % 1000000007;
}
memo[n][sum] = way;
return memo[n][sum];
}
public:
int numRollsToTarget(int n, int k, int target) {
memo = vector<vector<int>>(n + 1, vector<int>(target + 1, -1));
return bt(n, k, 0, target);
}
};Pramp - Number of Paths
4번째 Pramp mock interview경험.
잘 모르는 문제를 만나면 "이 문제 못풀겠다" 이런마음이 들수있는데, 처음에 막막해도 끝까지 붙잡고 있으면 어떻게든 풀게 된다는 사실을 다시한번 깨달음. 포기하지 않는게 중요!
문제
n x n 크기의 map이 있다고 할때, 좌-하단에서 우 상단까지 갈수 있는 경로의 경우의수는 무엇인가?(단 검은색 대각선기준 건너편(그림에서 검은색)은 이동할 수 없다.)
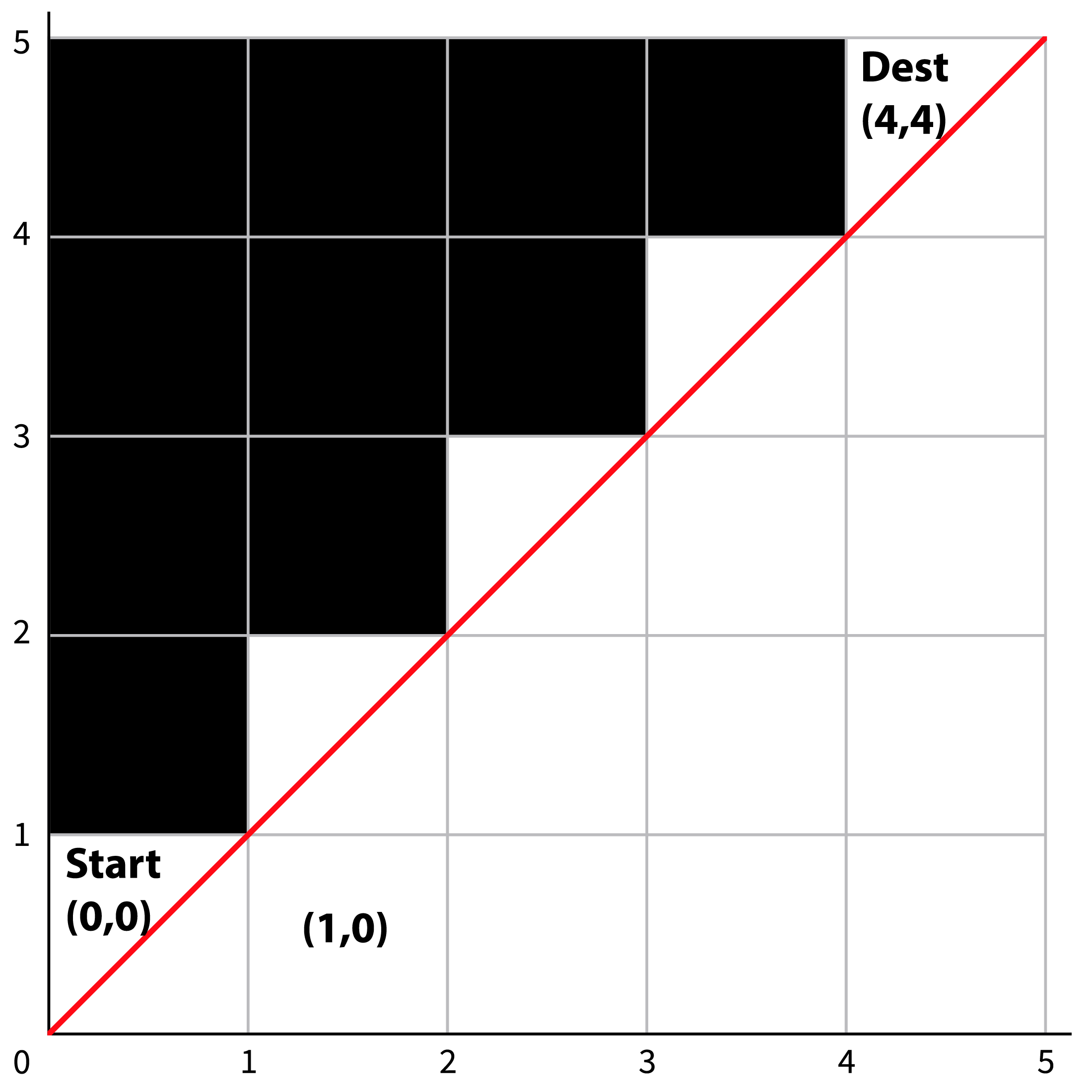
input: n = 4
output: 5해결 recursive
검은색의 존재를 처음부터 신경쓰면 당황할 수 밖에 없다. (처음에 당황). 하지만 일반 nxn크기의 맵에서 이동하는 경우의 수를 먼저 푼 뒤에, 나중에 검은색 영역은 어떻게 할지 처리하는 방향으로 풀이를 시작했다.
또한 좌-하단-> 우상단으로 이동하는게 배열인덱싱이 복잡하므로, 방향을 바꿔서 좌상단->우하단으로 이동하는걸로 생각했다. 어차피 답은 동일하니.
dfs recursive 함수가 경계를 만나면 0을 리턴하고 가장 외각길을 만나면 1을 리턴한다. ->이게 기본적인 nxn의 경우의수 이다. 여기서 r과 c의 관계를 한번 그려보면 대각선의 절반은 r > c가 된다는걸 알 수 있다(r < c도 가능). 아래 [] 의 경우 r > c인 관계가 성립되는것을 알 수 있다. 이 경우는 이동할 수 없는 경계이므로 0을 리턴한다.
0,0 0,1 0,2
[1,0] 1,1 1,2
[2,0] [2,1] 2,2int dfs(int r, int c) {
if (r < 0 || c < 0)
return 0;
if (r > c) // black area
return 0;
if (r == 0)
return 1
if (c == 0)
return 1;
// r c -> can describe black
// black area -> return 0
return dfs(r, c - 1) + dfs(r - 1, c);
}
int numOfPathsToDest(int n)
{
return dfs(n - 1, n - 1);
}
int main() {
printf("%d", dfs(3,3));
return 0;
}해결 DP
그리고 메모이제이션을 mem[][]을 통해 중복계산을 방지했다. 이건 추후에 풀이함. 인터뷰어가 노련했으면 이렇게 풀도록 가이드를 해줬을듯..(인터뷰어가 완전 생 초보였음..)
int mem[101][101];
int dfs(int r, int c) {
if (r < 0 || c < 0)
return 0;
if (r > c) // black area
return 0;
if (mem[r][c])
return mem[r][c];
if (r == 0 || c == 0)
return 1;
mem[r][c] = dfs(r, c - 1) + dfs(r - 1, c);
return mem[r][c];
}96. Unique Binary Search Trees
문제
1 ~ n 까지 값이 포함된 노드가 BST 가 되는 경우의 수를 구하라. 가령 n=3일때 총 5가지의 BST가 존재.

Input: n = 3
Output: 5아이디어
n=4 -> [1,2,3,4] 일때
총 갯수 = {
1이 루트일때 -> n=3 의 트리갯수
2가 루트일때 -> n=1의 트리갯수 * n=2의 트리갯수
3이 루트일때 -> n=2의 트리갯수 * n=1의 트리갯수
4가 루트일때 -> n=3의 트리갯수
} 를 더하면 됨.이를 수식으로 표현해보면 아래와 같은 규칙이 발견됨. 여기서 u[4]가 위의 계산결과가 됨. 해결 아이디어를 떠올리기 어려워서 솔루션을 조금 참고.
u[0] = 1
u[1] = 1
u[2] = u[1]*u[0] + u[0]*u[1]
u[3] = u[2]*u[0] + u[1]*u[1] + u[0]*u[2]
u[4] = u[3]*u[0] + u[2]*u[1] + u[1]*u[2] + u[0]*u[3]
u[5] = ...해결 DP
Runtime: 0 ms, faster than 100.00% of C
int numTrees(int n){
int uniq[20] = {};
uniq[0] = 1;
uniq[1] = 1;
for (int tgt = 2; tgt <= n; tgt++) {
for (int i = 0; i < tgt; i++) {
uniq[tgt] += uniq[tgt - i - 1] * uniq[i];
}
}
return uniq[n];
}139. Word Break
문제
주어진 문자열이 wordDict에 포함된 문자열로만 구성되어있는지 파악하라.
Input: s = "applepenapple", wordDict = ["apple","pen"]
Output: true
Input: s = "catsandog", wordDict = ["cats","dog","sand","and","cat"]
Output: falsehttps://leetcode.com/problems/word-break
해결 아이디어
문자열을 두부분으로 나누고 왼쪽이 hash table에 있는지 파악, 그리고 오른쪽은 recursive 함수가 결과를 리턴한다. 이것을 재귀적으로 반복.
"cat" "sandog"
^^^ ^^^^^^
true recursion
"sand" "og"
^^^^ ^^
true recursion -> false
"cats" "andog"
^^^^ ^^^^^
true recursion
"and" "dog"
^^^ ^^^
true recursion -> truebrute force
class Solution {
unordered_set<string> w_table;
int ssize;
bool recur(string s, int start) {
if (start == ssize)
return true;
for (int last = start + 1; last <= ssize; last++) {
if (w_table.find(s.substr(start, last - start)) == w_table.end())
continue;
if (recur(s, last))
return true;
}
return false;
}
public:
bool wordBreak(string s, vector<string>& wordDict) {
ssize = s.length();
for (auto a: wordDict)
w_table.insert(a);
return recur(s, 0);
}
};brute force + memoization
class Solution {
unordered_set<string> w_table;
int ssize;
vector<int> mem;
bool recur(string s, int start) {
if (start == ssize)
return true;
if (mem[start] != -1)
return mem[start];
for (int last = start + 1; last <= ssize; last++) {
if (w_table.find(s.substr(start, last - start)) == w_table.end())
continue;
if (recur(s, last)) {
mem[start] = true; // idx is start (not last)
return mem[start];
}
}
mem[start] = false;
return mem[start];
}
public:
bool wordBreak(string s, vector<string>& wordDict) {
ssize = s.length();
mem.assign(ssize, -1);
for (auto a: wordDict)
w_table.insert(a);
return recur(s, 0);
}
};64. Minimum Path Sum
문제
2차원 배열이 주어지고 좌상단에서 우하단으로 이동할때 가능한 경로중 최소비용은? (이동시 경로의 값을 더함)

Input: grid = [[1,3,1],[1,5,1],[4,2,1]]
Output: 7
Explanation: Because the path 1 → 3 → 1 → 1 → 1 minimizes the sum.해결
dp문제
#define min(a,b) (((a) < (b)) ? (a) : (b))
int mem[201][201];
int path_sum(int **grid, int row, int col) {
if (row < 0)
return -1;
if (col < 0)
return -1;
if (mem[row][col])
return mem[row][col];
int a = path_sum(grid, row - 1, col);
int b = path_sum(grid, row, col - 1);
if (a == -1 && b == -1) {
return grid[row][col];
} else if (b == -1) {
return a + grid[row][col];
} else if (a == -1) {
return b + grid[row][col];
}
mem[row][col] = min(a, b) + grid[row][col];
return mem[row][col];
}
int minPathSum(int** grid, int gridSize, int* gridColSize){
memset(mem, 0, sizeof(int) * 201 * 201);
return path_sum(grid, gridSize - 1, *gridColSize - 1);
}1387. Sort Integers by The Power Value
문제
값 x 주어질때 power값은 아래의 규칙을 따라 x가 1 이될때 까지의 step수를 의미한다.
- x가 짝수면 x = x / 2
- x가 홀수면 x = 3 * x + 1
예를 들어 x = 3 이면 power값은 7이다. (3 --> 10 --> 5 --> 16 --> 8 --> 4 --> 2 --> 1).
[lo, hi] 범위의 x값들이 주어질때. k 번째로 작은 power값의 x값은?
Input: lo = 12, hi = 15, k = 2
Output: 13
Explanation: The power of 12 is 9 (12 --> 6 --> 3 --> 10 --> 5 --> 16 --> 8 --> 4 --> 2 --> 1)
The power of 13 is 9
The power of 14 is 17
The power of 15 is 17
The interval sorted by the power value [12,13,14,15]. For k = 2 answer is the second element which is 13.
Notice that 12 and 13 have the same power value and we sorted them in ascending order. Same for 14 and 15.해결 dp top-down , O(nlogn)
특정 값의 power값은 모두 동일하므로 power값을 계산할때 memoization 하면 빠르게할수 있다. 그리고 계산 구조는 재귀적인 구조이다.
std::priority_queue 에 대해 새로 배운 것들
- priority_queue는 기본적으로 max heap이다. 이 문제에서는 min heap이어야하므로, 맨 마지막 인자에 greater<pair<int, int>> 를 추가한다. 이게 없으면 max heap.
- priority_queue는 pair자료형에서 first값을 기준으로 정렬한다.
class Solution {
int power_of_num(int val, int *dp) {
if (val == 1)
return 0;
if (dp[val])
return dp[val];
if (val % 2 == 0)
dp[val] = power_of_num(val / 2, dp) + 1;
else
dp[val] = power_of_num(val * 3 + 1, dp) + 1;
return dp[val];
}
public:
int getKth(int lo, int hi, int k) {
int ret = 0;
int dp[1000001] = {0};
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>> > pq;
for (int i = lo; i <= hi; i++)
pq.push(make_pair(power_of_num(i, dp), i));
while (k--) {
ret = pq.top().second;
pq.pop();
}
return ret;
}
};300. Longest Increasing Subsequence
문제
주어진 배열의 subsequence중에 값이 계속 증가하는것중 가장 긴 subsequence의 길이는?
Input: nums = [10,9,2,5,3,7,101,18]
Output: 4
Explanation: The longest increasing subsequence is [2,3,7,101], therefore the length is 4.https://leetcode.com/problems/longest-increasing-subsequence/
해결 DP - top down, O(N^2)
f(n) = max(f(n-1) ~ f(0)) (if < nums[n]) + 1
class Solution {
private:
int mem[2501];
int max_len_of(vector<int> nums, int idx) {
/* base case */
if (idx == 0)
return 1;
/* memoization */
if (mem[idx] != -1)
return mem[idx];
/* recursion */
int max = 0;
for (int i = idx - 1; i >= 0; i--) {
int prev_len = max_len_of(nums, i);
if (nums[i] < nums[idx]) {
if (prev_len > max)
max = prev_len;
}
}
mem[idx] = max + 1;
return mem[idx];
}
public:
int lengthOfLIS(vector<int>& nums) {
int most_largest = 0;
memset(mem, -1, sizeof(int) * nums.size());
mem[0] = 1;
max_len_of(nums, nums.size() - 1);
for (int i = 0; i < nums.size(); i++)
if (mem[i] > most_largest)
most_largest = mem[i];
return most_largest;
}
};해결 DP - bottom up, O(N^2)
솔루션 참고: 점화식 - dp[i] = max(dp[j] + 1) for all j where nums[j] < nums[i] and j < i
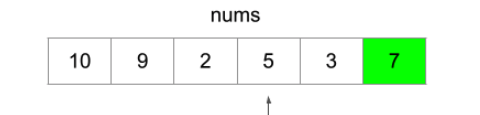
[i] 까지의 가장 긴 max 길이를 dp[]에 메모이제이션. 따라서 i를 고정하고 이전 인덱스에서 dp[j]와 비교함. 위 그림의 마지막 인덱스가 가질수 있는 subsequence의 경우의 수는 (2,5,7) 그리고 (2,3,7)이됨. 구조상 최소비용 계단오르기 문제와 비슷한것임.
점화식은 거의 동일하다. top down과 다르게 pass되었다. (422 ms, faster than 37.90% of C++)
class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
int nsize = nums.size();
int ret = 1;
vector<int> dp(nsize, 1);
for (int i = 0; i < nsize; i++) {
for (int j = i - 1; j >= 0; j--) {
if (nums[j] < nums[i]) {
dp[i] = std::max(dp[i], dp[j] + 1);
ret = std::max(ret, dp[i]);
}
}
}
return ret;
}
};198. House Robber
문제
프로페셔널 도둑에게 훔칠수 있는 돈이 기록된 집의 리스트 배열이 주어진다. 인접한 두 집을 한꺼번에 훔치면 경보가 작동해 잡혀간다. 잡혀가지 않고 최대로 많이 훔칠수 있는 금액은? (인접한 집은 배열의 바로 다음요소라는 의미)
Input: nums = [2,7,9,3,1]
Output: 12
Explanation: Rob house 1 (money = 2), rob house 3 (money = 9) and rob house 5 (money = 1).
Total amount you can rob = 2 + 9 + 1 = 12.https://leetcode.com/problems/house-robber/
해결 DP - bottom up - O(N^2)
두칸 이전 값부터 0번째까지 값중에 가장 큰값 + 현재 집 금액 을 더하는걸 반복하면 된다. 점화식을 아래와 같이 세워봤다.
초기값은 f(0) = nums[0], f(1) = nums[1]
f(n) = max(f(n-2) ~ f(0)) + nums(n)
뭔가 비효율적이다. DP라고 하더라도 시간복잡도가 O(N^2)이 되기 때문... (그런데도 채점 결과 100% faster가 나온건 의문)
int rob(int* nums, int numsSize){
if (numsSize == 1) return nums[0];
int *money = (int *)calloc(numsSize, sizeof(int));
money[0] = nums[0];
money[1] = nums[1];
int max_money = money[0] > money[1] ? money[0]: money[1];
for (int i = 2; i < numsSize; i++) {
int prev_max = 0;
for (int j = i - 2; j >= 0; j--) {
if (money[j] > prev_max)
prev_max = money[j];
}
money[i] = prev_max + nums[i];
if (money[i] > max_money)
max_money = money[i];
}
return max_money;
}해결 DP 점화식 개선
Discuss 중에 추천 글 -> How to approach most of DP problems.
DP문제 풀이의 정석임. 반드시 또 읽기!
This particular problem and most of others can be approached using the following sequence:
Find recursive relation
Recursive (top-down)
Recursive + memo (top-down)
Iterative + memo (bottom-up)
Iterative + N variables (bottom-up)if a problem is asking for the maximum/minimum/longest/shortest of something, the number of ways to do something, or if it is possible to reach a certain point, it is probably greedy or DP.
이 글을 읽고 개선된 점화식을 알게됐다. 강도가 현재 집 [i]에서 선택 할수 있는 행위는 두가지다.
- 1) 훔친다
- 2) 안훔친다
1)의 경우, 총 훔친 금액은 [i - 2] 까지 훔친 금액 + [i]에서 훔친 금액일것이고. 2)의경우는 [i-1] 까지 훔친 금액일 것이다. 이 두가지 중 더 큰값을 현재집의 총 훔친 금액으로 업데이트 하면 될것이다. 따라서 점화식은 다음과 같다.
f(i) = max(f(i-2) + curr_money, f(i - 1))그리고 문제에서 요구하는것이 마지막 집(i == n)에 도착할때 최대값이 아니라, 모든 경우의 수중 가장 큰 값으로 주어져서 점화식에서 마지막 값 f(n)을 구하는게 맞는건지 조금 햇갈렸는데. 그냥 점화식에서 f(n) 을 구하면 그게 최대값이된다. 최대값이 마지막까지 계속해서 누적되었기 때문이다.
풀이 1: DP top-down
memoization을 안해서 콜스택이 많이 쌓였을것, 당연히 Memory Limit Exceeded 발생!
class Solution {
private:
int rob_func(vector<int> nums, int idx) {
if (idx < 0)
return 0;
if (idx == 0)
return nums[0];
return std::max(rob_func(nums, idx - 2) + nums[idx], rob_func(nums, idx - 1));
}
public:
int rob(vector<int>& nums) {
return rob_func(nums, nums.size() - 1);
}
};풀이 2: DP top-down + Memoization (배열) - O(N)
만약 memset(mem, 0, sizeof(int) * 101); memoization 초기 배열값들을 0으로 초기화 하면 TLE발생! -1로 초기화하면 PASS 왜?
class Solution {
private:
int mem[101];
int rob_func(vector<int> nums, int idx) {
/* base case */
if (idx < 0)
return 0;
if (idx == 0)
return nums[0];
/* memoization */
if (mem[idx] != -1)
return mem[idx];
/* recursion */
mem[idx] = std::max(rob_func(nums, idx - 2) + nums[idx], rob_func(nums, idx - 1));
return mem[idx];
}
public:
int rob(vector<int>& nums) {
memset(mem, -1, sizeof(int) * 101);
return rob_func(nums, nums.size() - 1);
}
};풀이 2: DP top-down + Memoization (vector) - O(N)
vector 사용, 배열보다는 조금 느림.
class Solution {
private:
int rob_func(vector<int> nums, int idx, vector<int> &mem) {
/* base case */
if (idx < 0)
return 0;
if (idx == 0)
return nums[0];
/* memoization */
if (mem[idx] != -1)
return mem[idx];
/* recursion */
mem[idx] = std::max(rob_func(nums, idx - 2, mem) + nums[idx], rob_func(nums, idx - 1, mem));
return mem[idx];
}
public:
int rob(vector<int>& nums) {
vector<int> mem(nums.size(), -1);
return rob_func(nums, nums.size() - 1, mem);
}
};풀이 3: DP bottom-up - O(N)
마지막으로 bottom-up 풀이. 모든 DP문제는 top-down/bottom-up 둘다 해결 가능.
class Solution {
private:
int mem[101];
public:
int rob(vector<int>& nums) {
if (nums.size() == 1)
return nums[0];
memset(mem, -1, sizeof(int) * 101);
mem[0] = nums[0];
mem[1] = std::max(nums[0], nums[1]);
for (int i = 2; i < nums.size(); i++)
mem[i] = std::max(mem[i - 2] + nums[i], mem[i - 1]);
return mem[nums.size() - 1];
}
};62. Unique Paths
문제
mxn 크기의 맵이 주어질때 좌상단에서 우하단으로 갈수있는 모든 경우의 수를 구하기.
Input: m = 3, n = 7
Output: 28
https://leetcode.com/problems/unique-paths/
해결 brute force
우선 각각의 위치는 왼쪽칸 + 윗칸 값이 될것이다. 그리고 가장 코너칸의 값은 갈수있는방법이 1가지이기때문에 1이다. 그렇게 점화식을 세우면 다음과 같다.
f(m,n) = f(m-1, n) + f(m, n-1)
결과는 시간초과
/* brute force */
int uniquePaths(int m, int n){
/* base case */
if (m == 1 || n == 1) return 1;
/* recursive */
return uniquePaths(m - 1, n) + uniquePaths(m, n - 1);
}해결 DP top-down
visited[][] 배열에 계산된 값을 저장하는 memoization 으로 속도 개선.
/* DP top-down */
int visited[101][101];
int uniquePaths(int m, int n){
/* base case */
if (visited[m][n])
return visited[m][n];
if (m == 1 || n == 1) return 1;
/* recursive */
visited[m][n] = uniquePaths(m - 1, n) + uniquePaths(m, n - 1);
return visited[m][n];
}
해결 DP bottom-up
동일문제를 recursive가 아닌 for loop로 해결. 시간복잡도는 동일
/* DP bottom-up */
int uniquePaths(int m, int n){
int ret[101][101] = {0};
for (int i = 1; i <= m; i++)
ret[i][1] = 1;
for (int j = 1; j <= n; j++)
ret[1][j] = 1;
for (int i = 2; i <= m; i++) {
for (int j = 2; j <= n; j++) {
ret[i][j] = ret[i - 1][j] + ret[i][j - 1];
}
}
return ret[m][n];
}
322. Coin Change
문제
동전 종류가 주어질때, 동전을 조합하여 amount 값을 만들 수 있는 동전의 최소 갯수는? (동전 갯수는 무제한 제공된다고 가정)
Input: coins = [1,2,5], amount = 11
Output: 3
Explanation: 11 = 5 + 5 + 1https://leetcode.com/problems/coin-change/
해결 DP top down
int visit[10001];
int coin_amount(int* coins, int coinsSize, int amount){
int min_amt = INT_MAX;
int val = 0;
/* base case */
if (amount == 0)
return 0;
if (amount < 0)
return -1;
if (visit[amount])
return visit[amount];
/* recursion */
for (int i = 0; i < coinsSize; i++) {
val = coin_amount(coins, coinsSize, amount - coins[i]);
if (val != -1 && val < min_amt)
min_amt = val;
}
if (min_amt == INT_MAX)
visit[amount] = -1;
else
visit[amount] = min_amt + 1;
return visit[amount];
}
int coinChange(int* coins, int coinsSize, int amount){
memset(visit, 0, sizeof(int) * 10001);
return coin_amount(coins, coinsSize, amount);
}해결 DP bottom up
최종 amount 를 위한 동전들의 최소갯수와 최종 amount값에서 각각의 코인값을 뺀 값의 최소갯수가 계속 중복되는 형태이기 때문에 DP로 풀이가 가능하다. 이를 활용해 점화식을 구하면 아래와 같다.
f(n) = min( f(n - coins[0]), f(n - coins[1]), ... f(n - coins[k]) ) + 1만약 값이 [1,2,5] 라고 주어졌을때 3의 경우는 어떻게 구해야하지? 고민을 했고, 처음에는 다른 점화식을 사용해야한다고 생각해서 앞에서 따로 계산하려고 했다. 그래서 답이 안나왔다. 어쨋든 잘못된 방법이고. 점화식을 잘 세웠다면 첫번째 값부터 그 점화식으로 계산이 될것이다. 따라서 3의경우도 이 점화식으로 계산이 된다.
피보나치 수열같이 초기값들을 직접 계산할수 있는경우가 아니라면 항상 첫번째 값부터 점화식으로 계산하면 된다!
// [1,2,5]
// f(11) = min(f(11-1), f(11-2), f(11-5)) + 1;
// f(0) = 0
// f(1) = 1 = min( f(1-1), f(1-2), f(1-5)) + 1
// f(2) = 1 = min( f(2-1), f(2-2), f(2-5)) + 1
// f(3) = 2 = min( f(3-1), f(3-2), f(3-5)) + 1
// f(4) = 2 = min( f(4-1), f(4-2), f(4-5)) + 1int coinChange(int* coins, int coinsSize, int amount){
int *sum = (int *)calloc(amount + 1, sizeof(int));
for (int i = 1; i <= amount; i++) {
int min = INT_MAX;
int val = 0;
for (int c = 0; c < coinsSize; c++) {
val = i - coins[c];
if (val >= 0 && sum[val] != -1 && sum[val] < min)
min = sum[val];
}
if (min == INT_MAX)
sum[i] = -1;
else
sum[i] = min + 1;
}
return sum[amount];
}121. Best Time to Buy and Sell Stock
문제
idx가 날짜고, 값이 가격인 배열이 주어질때, 가장 쌀때 사서 비쌀때 판다고 할때 가장큰 수익은?
Input: prices = [7,1,5,3,6,4]
Output: 5
Explanation: Buy on day 2 (price = 1) and sell on day 5 (price = 6), profit = 6-1 = 5.
Note that buying on day 2 and selling on day 1 is not allowed because you must buy before you sell.해결
#define max(a,b) (((a) > (b)) ? (a) : (b))
int maxProfit(int* prices, int pricesSize){
int min_val = INT_MAX;
int max_val = 0;
for (int i = 0; i < pricesSize; i++) {
if (prices[i] < min_val)
min_val = prices[i];
else
max_val = max(prices[i] - min_val, max_val);
}
return max_val;
}118. Pascal's Triangle
문제
다음과 같은 Pascal's Triangle 결과를 출력하기
Input: numRows = 5
Output: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]
https://leetcode.com/problems/pascals-triangle/
해결
int** generate(int numRows, int* returnSize, int** returnColumnSizes){
int **ret = (int **)malloc(sizeof(int *) * numRows);
*returnColumnSizes = (int *)calloc(numRows, sizeof(int));
*returnSize = numRows;
for (int i = 0; i < numRows; i++) {
ret[i] = (int *)malloc(sizeof(int) * (i + 1));
(*returnColumnSizes)[i] = i + 1;
for (int j = 0; j < i + 1; j++) {
if (j == 0 || j == i) {
ret[i][j] = 1;
continue;
}
ret[i][j] = ret[i - 1][j - 1] + ret[i - 1][j];
}
}
return ret;
}119. Pascal's Triangle II
문제
Pascal's Triangle의 주어진 rowIndex값 번째의 행을 리턴하기
Input: rowIndex = 3
Output: [1,3,3,1]
https://leetcode.com/problems/pascals-triangle-ii/
해결 O(N) / O(N)
1번문제에서는 공간복잡도가 N^2였는데 이번에는 O(N)에 해결됨.
int* getRow(int rowIndex, int* returnSize){
*returnSize = rowIndex + 1;
int *ret = malloc(sizeof(int) * (*returnSize));
for (int i = 0; i < (*returnSize); i++)
ret[i] = 1;
for (int i = 1; i < rowIndex; i++)
for (int j = i; j > 0; j--)
ret[j] = ret[j-1] + ret[j];
return ret;
}70. Climbing Stairs
문제
계단을 한칸 혹은 두칸씩 오를 수 있다고 할때, n번째 계단을 오르는 경우의 수는?
https://leetcode.com/problems/climbing-stairs/
유사문제
- 746. Min Cost Climbing Stairs
계단을 오르는 최소비용값 이라는 차이가 있음.
해결 O(N)
이런 문제는 base case값만 잘 생각해서 리턴하면 최종값은 자동으로 계산됨. dp의 memoization을 사용하면 O(N)에 해결.
헉 다풀고 보니 풀이가 피보나치 수열과 동일하다.
1. constraints
- 1 <= n <= 45
2. Ideas
- DP
- dp[] = how many way
- dp[n] = dp[n-1] + dp[n-2] (dp[1] == 1, dp[2] == 2)
3. Test cases
- assert(recur(1) = 1)
- assert(recur(2) = 2)
- assert(recur(3) = 3)
- assert(recur(4) = 5)int dp[46];
int climbStairs(int n){
if (dp[n])
return dp[n];
if (n == 1)
return 1;
if (n == 2)
return 2;
dp[n] = climbStairs(n - 1) + climbStairs(n - 2);
return dp[n];
}746. Min Cost Climbing Stairs
문제
각 계단을 오르는 비용을 나타내는 배열이 주어진다. 계단은 1칸 혹은 2칸씩 오를 수 있다. 최소의 비용으로 꼭데기 까지 오른다면 얼마가 드는가?
Input: cost = [10,15,20]
Output: 15해결 : DP O(N)
r(n) = min(재귀(n-1), 재귀(n-2))형식의 min/max 를 구하는 재귀 + DP 문제.
cost 배열이 [10, 15, 20] 이렇게 주어졌을때 점화식이 dp[n] = cost[n] + min(dp[n-1], dp[n-2]) 이라면, cost[3] 는 존재하지 않기 때문에 재귀함수 내에서 접근하면 런타임에러가 발생한다. 이런 경우는 애초에 리턴값계산에 재귀함수를 두 번 호출하는게 좋다. return min(recur(n-1), recur(n-2))
1. Constraints
- the stair start from left to right? -> yes
- the cost value 0 <= cost[i] <= 999
- 2 <= cost.length <= 1000
2. Ideas
- DP
dp[n] = cost[n] + min(dp[n-1], dp[n-2])
3. Test Cases
- min lenth input
-
4. Coding
#define min(a, b) (((a) < (b)) ? (a) : (b))
int target;
int recur(int *c, int *dp, int n)
{
if (dp[n])
return dp[n];
/* base case */
if (n == 0)
return c[0];
if (n == 1)
return c[1];
/* recursion */
dp[n] = c[n] + min(recur(c, dp, n - 1), recur(c, dp, n - 2));
return dp[n];
}
int minCostClimbingStairs(int* cost, int costSize){
int dp[1000] = {0};
return min(recur(cost, dp, costSize - 1), recur(cost, dp, costSize - 2));
}338. Counting Bits
n 값이 주어졌을때, 0 ~ n 의 숫자의 2진수에서 1의 갯수를 구하고 배열로 리턴하기
Input: n = 5
Output: [0,1,1,2,1,2]
Explanation: 0 --> 0 1 --> 1 2 --> 10 3 --> 11 4 --> 100 5 --> 101https://leetcode.com/problems/counting-bits/
O(n log n)
int* countBits(int n, int* returnSize){
*returnSize = n + 1;
//int *ret = (int *)malloc(sizeof(int) * *returnSize);
int *ret = (int *)calloc(*returnSize, sizeof(int));
for (int i = 0; i <= n; i++) {
int bitval = i;
while (bitval != 0) {
if ((bitval & 1) == 1)
ret[i]++;
bitval = bitval >> 1;
}
}
return ret;
}O(n)
DP로 해결 점화식 : ret[n] = 1 + ret[n - a]
아래와 같은 규칙을 통해서 점화식 도출 a는 2의 배수 값이고 2진수의 자릿수의 첫번째 수에 해당하는 값임 (1 10 100 1000 ...)
재미있는 문제였음. discussion보면 더 빠른 방법으로 점화식을 도출했던데 나는 다른방식으로 점화식을 세워봤음.
0000 ret[0] = 0
0001 ret[1] = 1 + ret[1 - 1]
0010 ret[2] = 1 + ret[2 - 2]
0011 ret[3] = 1 + ret[3 - 2]
0100 ret[4] = 1 + ret[4 - 4]
0101 ret[5] = 1 + ret[5 - 4]
0110 ret[6] = 1 + ret[6 - 4]
0111 ret[7] = 1 + ret[7 - 4]
1000 ret[8] = 1 + ret[8 - 8]
1001 ret[9] = 1 + ret[9 - 8]
1010 ret[10] = 1 + ret[10 - 8]
...
1111 ret[15] = 1 + ret[15 - 8]int* countBits(int n, int* returnSize){
*returnSize = n + 1;
int *ret = (int *)calloc(*returnSize, sizeof(int));
ret[0] = 0;
if (n == 0)
return ret;
for (int i = 1; i <= n; i++) {
int a = 1;
for (int val = i; val > 1;) {
val >>= 1;
a <<= 1;
}
ret[i] = 1 + ret[i - a];
}
return ret;
}1137. N-th Tribonacci Number
문제
다음을 만족하는 Tribonacci 수열이 존재할때 값을 계산하기.
T0 = 0, T1 = 1, T2 = 1, and Tn+3 = Tn + Tn+1 + Tn+2 for n >= 0.https://leetcode.com/problems/n-th-tribonacci-number/
해결 O(N)
재귀를 배울때 항상나오는 피보나치 + DP 문제와 동일. dp[] 배열에 결과를 저장하면 함수콜을 할 필요없이 이미 한번 계산했던것은 배열값을 쓰면 됨. 시간복잡도는 O(N).
추가로, 모든 테스트케이스에서 모든 입력값들의 dp[i]는 동일하기 때문에, 전역변수로 써도됨.(오히려 테스트케이스가 누적될수록 겁나 빠른 결과가 나온다. 개이득인 부분) 그래서 결과도 겁나 빠르게 나옴 100%.
Runtime: 0 ms, faster than 100.00% of C online submissions for N-th Tribonacci Number.
Memory Usage: 5.4 MB, less than 97.69% of C online submissions for N-th Tribonacci Number.1. Constraints.
- input size: 0 <= n <= 37
- return type: int
-
2. Ideas
- DP + memoization -> O(N) / O(N)
- dp[n] is same on the every test case input n
3. Test Cases
- assert(tribonacci(0) == 0)
- assert(tribonacci(1) == 1)
- assert(tribonacci(2) == 1)
- assert(tribonacci(3) == 2)
- assert(tribonacci(25) == 1389537)
4. Coding그리고 dp[n] 값 리턴하는 라인을 가장 먼저하는게 더 빠르다.
int dp[38] = {0};
int tribonacci(int n){
if (dp[n])
return dp[n];
if (n == 0)
return 0;
if (n == 1 || n == 2)
return 1;
dp[n] = tribonacci(n-1) + tribonacci(n-2) + tribonacci(n-3);
return dp[n];
}509. Fibonacci Number
피보나치 수열의 합 구하기
Input: n = 4
Output: 3
Explanation: F(4) = F(3) + F(2) = 2 + 1 = 3.int fib(int n){
if (n == 0)
return 0;
if (n == 1)
return 1;
return fib(n - 1) + fib(n - 2);
}