문제
주어진 배열의 subsequence중에 값이 계속 증가하는것중 가장 긴 subsequence의 길이는?
Input: nums = [10,9,2,5,3,7,101,18]
Output: 4
Explanation: The longest increasing subsequence is [2,3,7,101], therefore the length is 4.https://leetcode.com/problems/longest-increasing-subsequence/
해결 DP - top down, O(N^2)
f(n) = max(f(n-1) ~ f(0)) (if < nums[n]) + 1
class Solution {
private:
int mem[2501];
int max_len_of(vector<int> nums, int idx) {
/* base case */
if (idx == 0)
return 1;
/* memoization */
if (mem[idx] != -1)
return mem[idx];
/* recursion */
int max = 0;
for (int i = idx - 1; i >= 0; i--) {
int prev_len = max_len_of(nums, i);
if (nums[i] < nums[idx]) {
if (prev_len > max)
max = prev_len;
}
}
mem[idx] = max + 1;
return mem[idx];
}
public:
int lengthOfLIS(vector<int>& nums) {
int most_largest = 0;
memset(mem, -1, sizeof(int) * nums.size());
mem[0] = 1;
max_len_of(nums, nums.size() - 1);
for (int i = 0; i < nums.size(); i++)
if (mem[i] > most_largest)
most_largest = mem[i];
return most_largest;
}
};해결 DP - bottom up, O(N^2)
솔루션 참고: 점화식 - mem[i] = max(mem[j] + 1) for all j where nums[j] < nums[i] and j < i
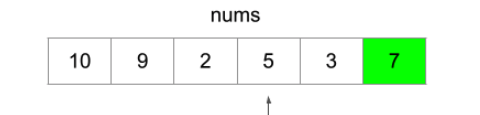
[i] 까지의 가장 긴 max 길이를 mem[]에 메모이제이션. 따라서 i를 고정하고 이전 인덱스에서 mem[j]와 비교함. 위 그림의 마지막 인덱스가 가질수 있는 subsequence의 경우의 수는 (2,5,7) 그리고 (2,3,7)이됨. 구조상 최소비용 계단오르기 문제와 비슷한것임.
점화식은 거의 동일하다. top down과 다르게 pass되었다. (422 ms, faster than 37.90% of C++)
class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
int maxlen = 1;
vector<int> mem(nums.size(), 1);
for (int i = 0; i < nums.size(); i++) {
for (int j = 0; j < i; j++) {
if (nums[j] < nums[i]) {
mem[i] = std::max(mem[i], mem[j] + 1);
}
}
maxlen = std::max(maxlen, mem[i]);
}
return maxlen;
}
};해결 O(n^2)
230221 풀어봄. 풀이 참고 하였는데 아주 재밌는(?) 알고리즘. 이 알고리즘은 혼자서는 알아내지 못했을것같음.
- 새로운 sub배열(정렬된)을 생성하는 방법. sub배열의 크기가 LIS임
20 100 10 12 5 13
20 sub 배열에 첫번째 값추가
20 100 nums의 다음 값이 sub의 마지막 값보다 크면 sub 배열에 추가
10 100 nums의 다음 값이 sub의 마지막 값보다 작다면 sub배열의 앞에서부터 자신보다 바로 다음 큰값을 찾고 교체
10 12 위의 알고리즘 반복
5 12
5 12 13 최종적으로 sub의 크기가 최대 LIS값이 된다. class Solution {
public:
int lengthOfLIS(vector<int>& nums) {
vector<int> sub;
sub.push_back(nums[0]);
for (int i = 1; i < nums.size(); i++) {
if (sub[sub.size() - 1] < nums[i]) {
sub.push_back(nums[i]);
} else {
int j = 0;
while (sub[j] < nums[i]) j++;
sub[j] = nums[i];
}
}
return sub.size();
}
};
해결 O(nlogn)
230226 위의 sub 배열 생성방법에서 sub[j]값을 nums[i]로 대체할때 sub배열을 순차적으로 탐색했는데, sub는 정렬된 배열이므로 binary search하면 O(logn)으로 탐색할 수 있다. 한가지 실수한 부분은 binary search 구현부분에서 right = mid인데, 코드를 제출하기 전에 간단한 예제로 뇌 컴파일을 해봤어야했다.
아래 예제에서 b의 경우는 right = mid + 1 일때, 1을 찾게 된다.
a: 1 2 3 5 (target: 4)
b: 1 3 5 7 (target: 2) class Solution {
int binary_search(vector<int> &nums, int tgt) {
int left = 0;
int right = nums.size() - 1;
// 1 2 3 5 (4)
// 1 3 5 7 (2)
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] == tgt) {
return mid;
} else if (nums[mid] < tgt) {
left = mid + 1;
} else {
right = mid;
}
}
return left;
}
public:
int lengthOfLIS(vector<int>& nums) {
vector<int> sub;
sub.push_back(nums[0]);
for (int i = 0; i < nums.size(); i++) {
if (sub[sub.size()-1] < nums[i]) {
sub.push_back(nums[i]);
} else {
int j = binary_search(sub, nums[i]);
sub[j] = nums[i];
}
}
return sub.size();
}
};Functional Programming 스타일
다음은 DP(bottom-up) O(n^2)풀이를 함수형 프로그래밍 스타일로 변경한것 언어는 Scala (.feat chatGPT)
230726 작성
아래는 주어진 C++ 코드를 Scala 언어로 변경한 functional programming 스타일의 코드입니다. Scala는 함수형 프로그래밍과 객체지향 프로그래밍을 모두 지원하기 때문에, 이를 이용하여 간결하고 효율적인 코드를 작성할 수 있습니다.
Copy code
object Solution {
def lengthOfLIS(nums: Array[Int]): Int = {
def lisRec(idx: Int, mem: Array[Int]): Int = {
if (idx == 0) 1
else {
val maxLength = (0 until idx)
.filter(j => nums(j) < nums(idx))
.map(j => 1 + lisRec(j, mem))
.foldLeft(1)(_ max _)
mem(idx) = maxLength
maxLength
}
}
val mem = Array.fill(nums.length)(-1)
(0 until nums.length).map(i => lisRec(i, mem)).max
}
}이 코드는 내부적으로 재귀 함수를 사용하여 longest increasing subsequence를 찾습니다. lisRec 함수는 주어진 인덱스에서 시작하는 LIS의 길이를 계산합니다. 결과는 mem 배열에 저장되어 중복 계산을 피합니다. foldLeft 함수를 사용하여 최대 길이를 찾습니다.
예제:
Copy code
val nums = Array(10, 9, 2, 5, 3, 7, 101, 18)
println(Solution.lengthOfLIS(nums)) // Output: 4주어진 C++ 코드와 동일한 동작을 합니다. 하지만 Scala는 더욱 함수형 프로그래밍 스타일에 적합한 언어이므로 더 간결하고 명확한 코드를 작성할 수 있습니다.
