Pramp - Number of Paths

4번째 Pramp mock interview경험.

잘 모르는 문제를 만나면 "이 문제 못풀겠다" 이런마음이 들수있는데, 처음에 막막해도 끝까지 붙잡고 있으면 어떻게든 풀게 된다는 사실을 다시한번 깨달음. 포기하지 않는게 중요!

문제

n x n 크기의 map이 있다고 할때, 좌-하단에서 우 상단까지 갈수 있는 경로의 경우의수는 무엇인가?(단 검은색 대각선기준 건너편(그림에서 검은색)은 이동할 수 없다.)

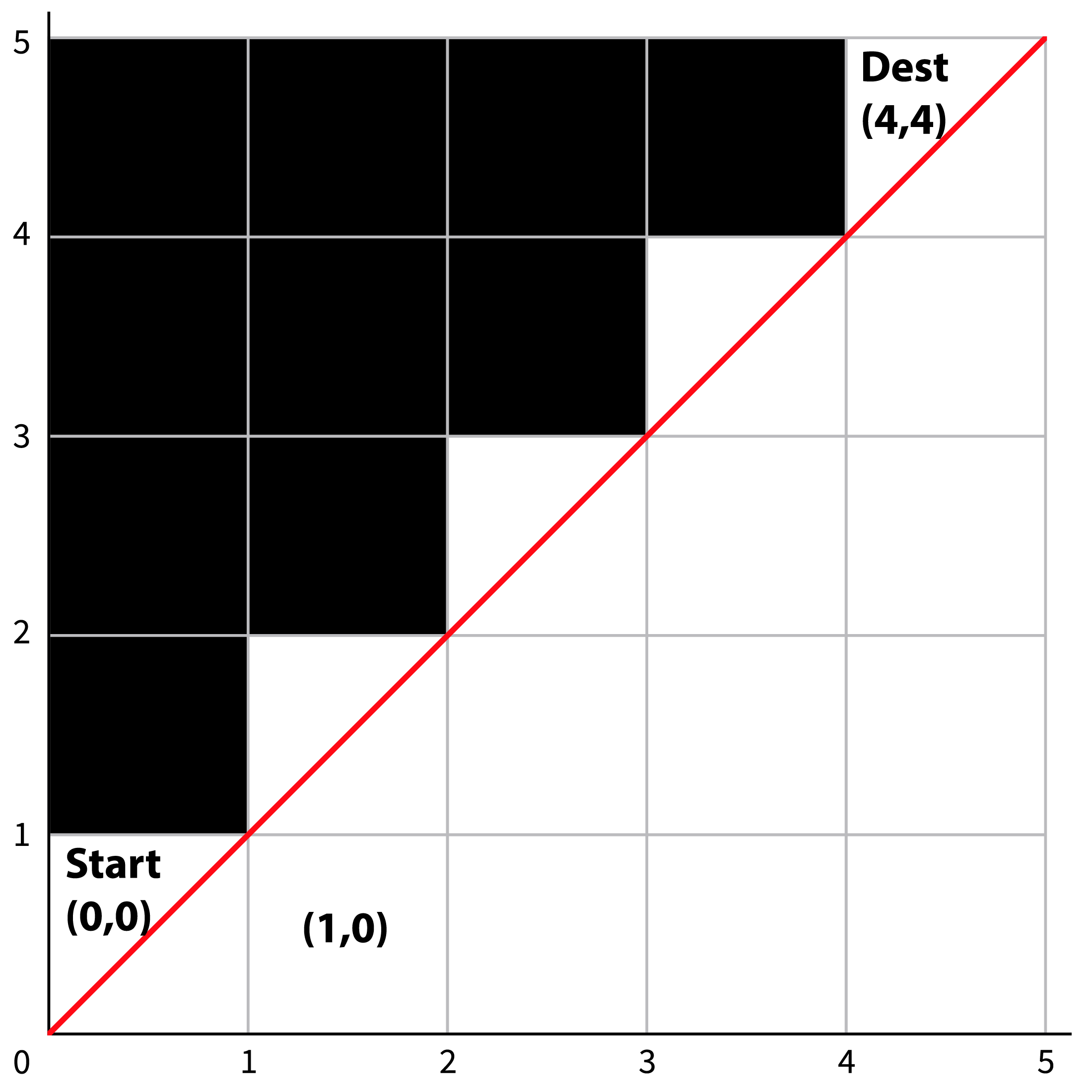
input:  n = 4
output: 5

해결 recursive

검은색의 존재를 처음부터 신경쓰면 당황할 수 밖에 없다. (처음에 당황). 하지만 일반 nxn크기의 맵에서 이동하는 경우의 수를 먼저 푼 뒤에, 나중에 검은색 영역은 어떻게 할지 처리하는 방향으로 풀이를 시작했다.

또한 좌-하단-> 우상단으로 이동하는게 배열인덱싱이 복잡하므로, 방향을 바꿔서 좌상단->우하단으로 이동하는걸로 생각했다. 어차피 답은 동일하니.

dfs recursive 함수가 경계를 만나면 0을 리턴하고 가장 외각길을 만나면 1을 리턴한다. ->이게 기본적인 nxn의 경우의수 이다. 여기서 r과 c의 관계를 한번 그려보면 대각선의 절반은 r > c가 된다는걸 알 수 있다(r < c도 가능). 아래 [] 의 경우 r > c인 관계가 성립되는것을 알 수 있다. 이 경우는 이동할 수 없는 경계이므로 0을 리턴한다.

 0,0   0,1  0,2
[1,0]  1,1  1,2
[2,0] [2,1] 2,2

int dfs(int r, int c) {
    if (r < 0 || c < 0)
      return 0;
    if (r > c) // black area
      return 0;
    if (r == 0)
      return 1
    if (c == 0)
      return 1;
    // r c -> can describe black 
    // black area -> return 0 

    return dfs(r, c - 1) + dfs(r - 1, c);
}

int numOfPathsToDest(int n) 
{
   return dfs(n - 1, n - 1);
}

int main() {
  printf("%d", dfs(3,3));
  return 0;
}

해결 DP

그리고 메모이제이션을 mem[][]을 통해 중복계산을 방지했다. 이건 추후에 풀이함. 인터뷰어가 노련했으면 이렇게 풀도록 가이드를 해줬을듯..(인터뷰어가 완전 생 초보였음..)

int mem[101][101];

int dfs(int r, int c) {
    if (r < 0 || c < 0)
      return 0;
    if (r > c) // black area
      return 0;
    if (mem[r][c])
      return mem[r][c];
    if (r == 0 || c == 0)
      return 1;

    mem[r][c] = dfs(r, c - 1) + dfs(r - 1, c);
    return mem[r][c];
}