[DS] Graph

soor.dev·2021년 4월 23일

data structure

Data structure

목록 보기

4/4

저 말고 이 글을 보실 분이 있을지는 모르겠지만..허헛.. 혹시 수정해야할 부분이 있다면 댓글로 말씀 해 주시면 감사하겠습니다!! 🙇🏻‍♀️

Graph

그래프하면 엑셀에서 주로 쓰는 표, x축, y축이 존재하는 비례 반비례 그래프 등이 먼저 생각난다. 하지만 자료구조 그래프는 아래 이미지와 같이 여러개의 점들이 선으로 복잡하게 연결되어 있는 모습을 하고있다.

1과 5, 또는 1과 2처럼 1과 직접적으로 연결되어 있는 점도 있는 방면에 1과 4처럼 5를 통해 연결되어 있는 점들도 있다. 여기서 숫자가 적힌 점들을 vertex(정점), 선은 edge(간선) 이라고 표현한다.

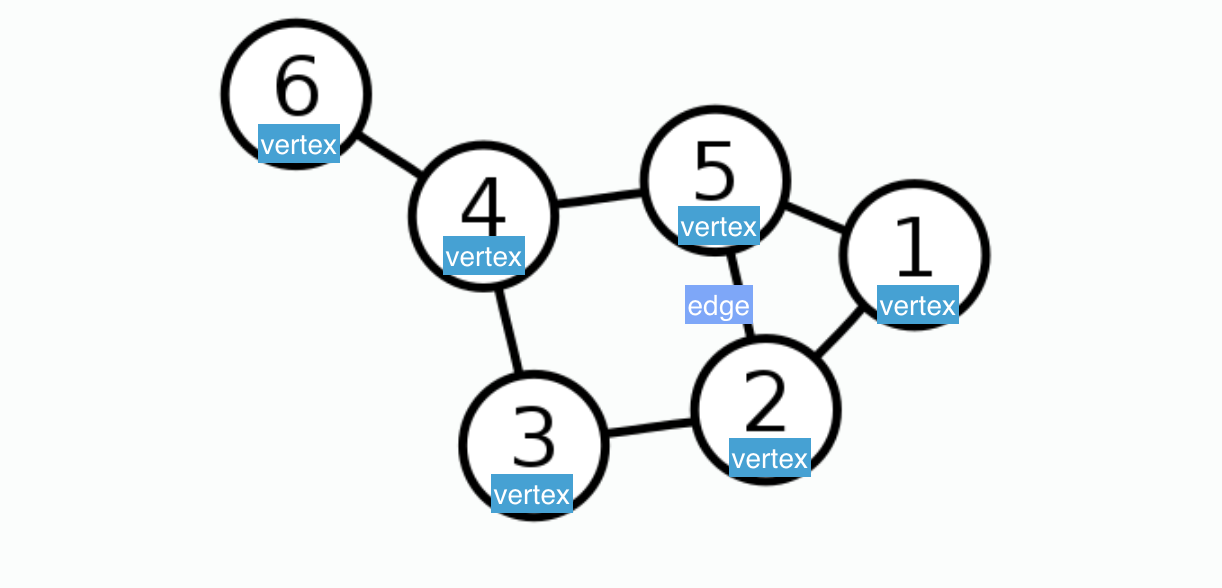
Graph 관련 용어들

undirected graph & directed graph

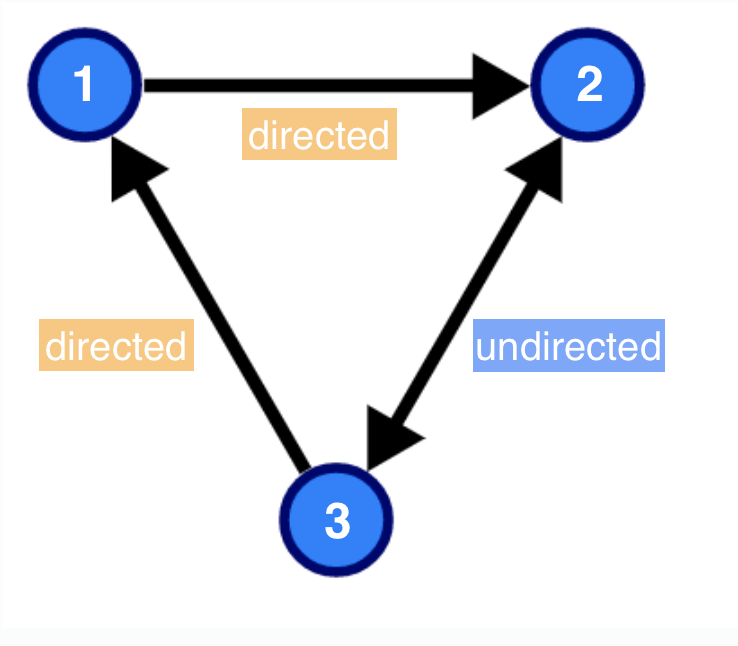
undirected? 방향이 없는? 이라고 생각해서 헷갈렸는데, 쌍방향이라고 생각해도 무방할지는 모르겠지만(?) 나는 쉽게 이해하려고 그렇게 생각하고 있다. 첨부한 이미지에서 2와 3은 서로를 이어주고 있다. 이를 undirected graph (무향 그래프) 라고 한다. 하지만 1과 2를 보면, 1에서 2는 간선이 있지만, 2에서 1로 향하는 간선은 없는 것이다. 이처럼 간선이 양방향으로 있지않고, 한 방향으로만 있는 것을 directed graph (단방향 그래프) 라고 한다. 단방향 그래프는 완전 일방통행인 것이다.

self loop & cycle

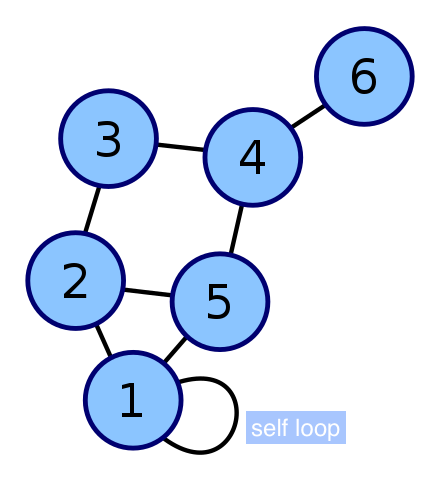
self loop 는 정점에서 진출하는 간선이 곧바로 자기 자신에게 진입하는 경우를 말한다. 다른 정점을 거치지 않고 바로 자기 자신에게 돌아오는 경우이다. 위의 이미지에서 1은 self loop를 갖고있다.

cycle 은 한 정점에서 출발하여 다시 돌아올 수 있다면 cycle이 있다고 말한다.

in-degree & out-degree

한 정점에 진입하고 in-degree(진입차수), 나가는 out-degree(진출차수) 간선이 몇 개인지를 나타낸다.

Graph 표현방식

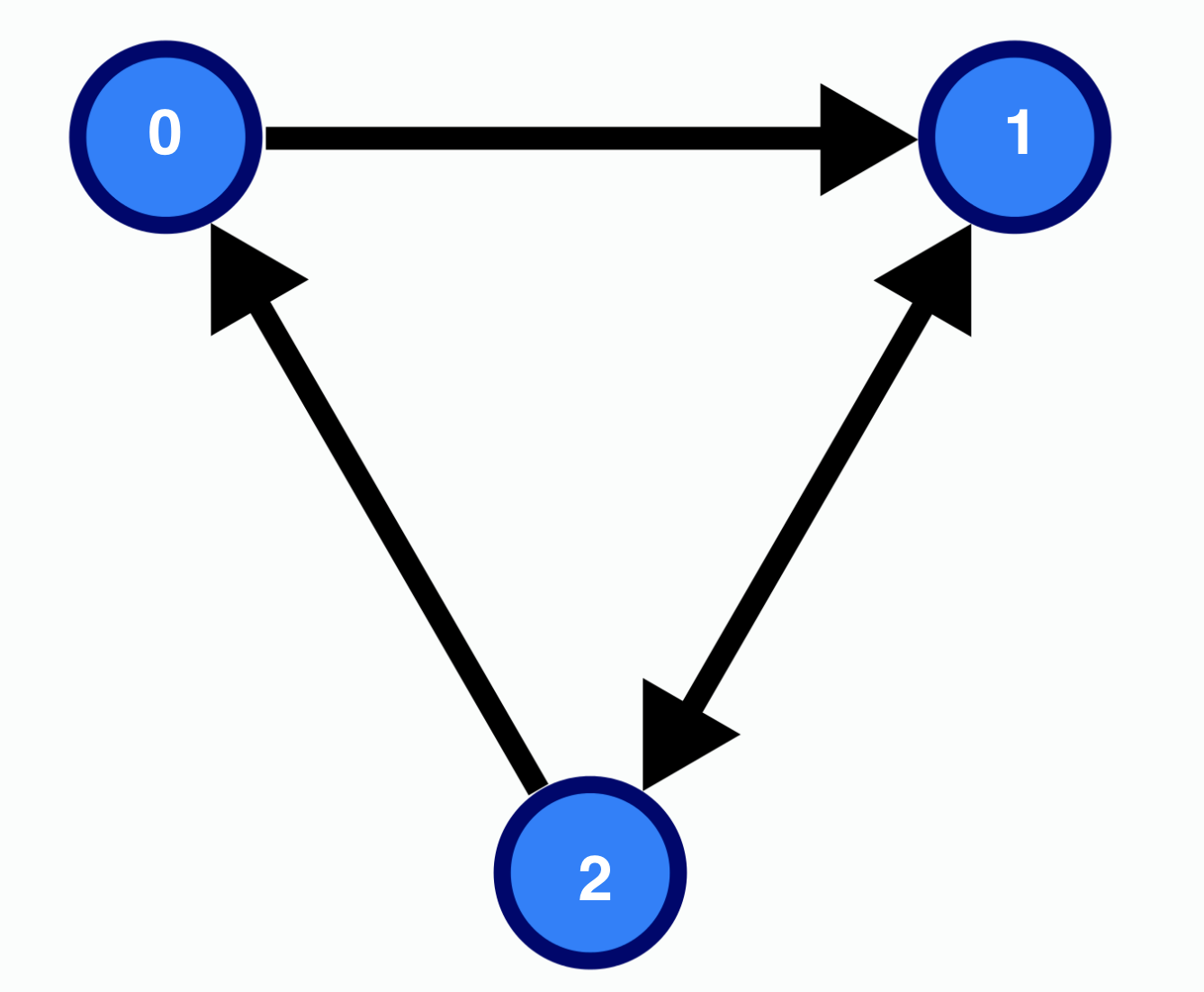
✅ Adjancency(인접) : 두 정점간에 간선이 직접 이어져 있다면 이 두 정점은 인접한 정점

Adjancency matrix

인접행렬
인접한 정점들간의 인접함(간선)을 표시해 주는 행렬로, 2차원 배열의 모습이다. 이어져 있다면 1, 이어져 있지 않다면 0으로 표시한다. 위의 그래프를 인접행렬로 표시한다면 아래와 같다. 정점은 adjMatrix[i]가 될 것이고, 각 배열요소 안에 0과 1로 표시된 요소들은 간선이 된다.
표의 형태와 비슷하며, 인접하지 않은 정보도 전부 확인이 되기 때문에 보기에는 편할 수 있지만 필요하지 않은 정보도 읽어야 한다는 단점이 있을 수도 있ㄸ.

let adjMatrix = [
              To
     	     0  1  2   
From      0 [0, 1, 0]
	  1 [0, 0, 1]
 	  2 [1, 1, 0]
]

인접행렬 - JS 코드 구현

function createMatrix(edges) {
  // 1) 가장 큰 수를 갖는 정점 찾기
  let max = edges.flat().filter((el) => typeof el === 'number');
  max = Math.max(...max);
  // 2) 0 ~ 1)에서 찾은 정점까지의 크기를 갖는 매트릭스 만들기
  let matrix = Array(max + 1).fill(0).map((row) => Array(max + 1).fill(0));

  // 3) 정점을 만들었으니, 연결되는 간선을 만들어줌
  for(let i = 0; i < edges.length; i++) {
    let [row, col, direction] = edges[i];
    if(direction === 'directed') {
      matrix[row][col] = 1;
    }
    else if(direction === 'undirected') {
      matrix[row][col] = 1;
      matrix[col][row] = 1;
    }
  }
  return matrix;
}

let output1 = createMatrix([
	[0, 3, "directed"],
	[0, 2, "directed"],
	[1, 3, "directed"],
	[2, 1, "directed"],
]);

console.log(output1);
/**
 * [
 *  [0, 0, 1, 1],
 *  [0, 0, 0, 1],
 *  [0, 1, 0, 0],
 *  [0, 0, 0, 0]
 * ]
 */

Adjacency list

인접리스트
각 정점과 어떤 정점이 인접한지를 리스트 형태로 표시한 것이며, 리스트 안에는 자신과 인접한 다른 정점이 값으로 들어온다.

let adjList = {0: [1], 1 : [2], 2 : [0, 1]};

인접행렬은 모든 경우의 수를 저장하기 때문에 메모리를 많이 차지한다. 메모리를 효율적으로 사용하고 싶을 때 인접리스트를 사용해보자!!

Graph 탐색

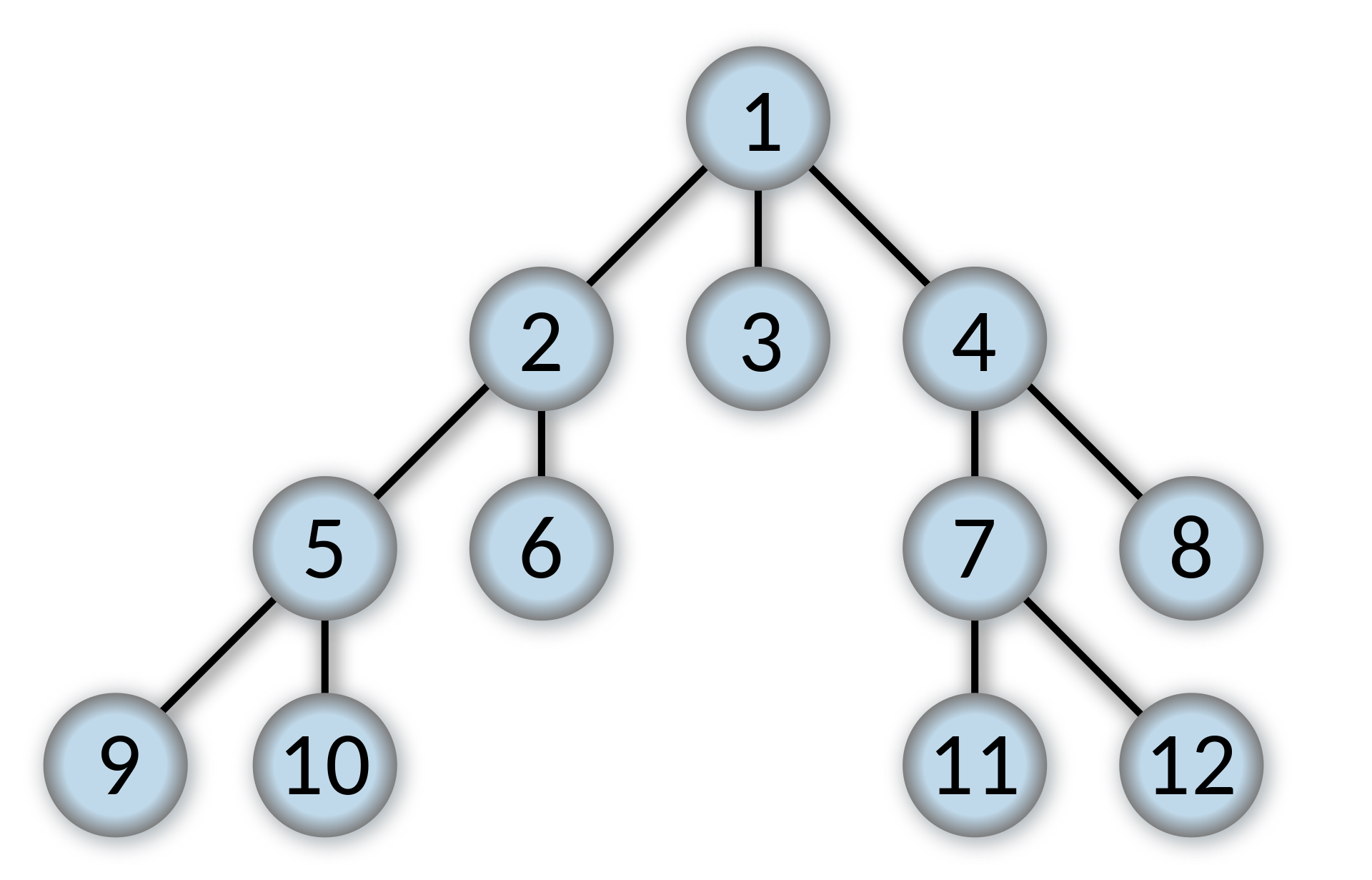
BFS

너비 우선 탐색 방법(Breadth-First-Search)
1-2-3-4-5-6-7-8-9-10-11-12 순서로 탐색

시작 정점으로부터 가까운 정점들을 다 탐색하고, 그 다음 정점들을 탐색하는 방법이다.
두 정점 사이의 최단 경로를 찾고 싶을 때 사용한다.
그래프 탐색시 이미 탐색한 노드는 표시해 두어야 무한루프에 빠지지 않는다.
차례대로 저장한 후, 먼저 저장한 것부터 꺼낼 수 있는 구조인 queue를 사용하며, 재귀를 사용하지 않는다.

DFS

깊이 우선 탐색 방법 DFS(depth-first search)
1-2-5-9-10-6-3-4-7-11-8-12 순서로 탐색

자기 자신을 호출하는 순환 알고리즘의 형태로, 루트노드에서 시작해서 한 방향으로 계속 가다가 더 이상 길이 없을 때, 가장 가까운 갈림길로 돌아와서 다시 한 방향으로 탐색하는 방법이다. (stack을 사용하며 재귀로 움직인다)
BFS보다 좀 더 간단하지만, 단순검색 시, BFS보다 느리다.
그래프 탐색시 이미 탐색한 노드는 표시해 두어야 무한루프에 빠지지 않는다.
모든 노드를 방문하고자 할 때 쓰인다.

Reference

image - wiki
BFS & DFS

soor.dev

이전 포스트