Tree

나무가 뿌리를 내리고 있는 모습을 떠올리면, 한 뿌리에서 나아가 가지가 생기고, 잎이 무성해지는 장면이 떠오른다. 트리구조는 이를 거꾸로 놓은 모습을 가지고 있으며, 그래프의 여러 구조 중 일방향 그래프의 한 구조이다.

트리구조를 공부하면서 굉장히 많이 쓰일 것 같다는 생각을 했는데, 어떤 데이터 안에 또 데이터가 목록을 이루고, 또 하위항목을 갖고, 갖고, 갖고... Desktop/download/file_1/file_1_1/file1_1_1 과 같은 형태로 컴퓨터에서 디렉토리 구조를 생각할 수 있을 것이다.

---

Binary Tree

자식 노드가 최대 2개인 노드들로 구성된 트리구조를 이진트리(Binary Tree) 라고 한다. (왼쪽 자식 & 오른쪽 자식)

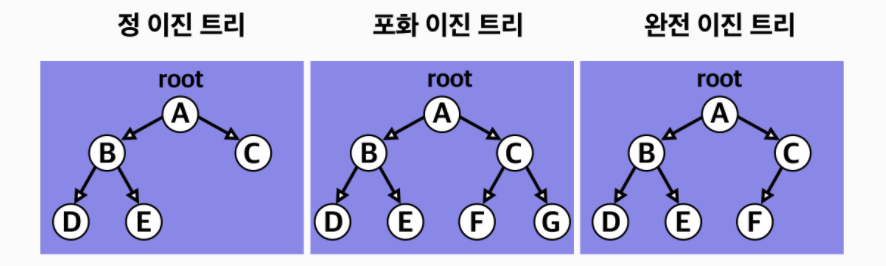
• 정 이진 트리 : 각 노드가 0개 혹은 2개의 자식 노드를 갖는다.
• 포화 이진 트리 : 정 이진 트리이면서 완전 이진트리인 경우, 모든 레벨이 가득 채워져 있다.
• 완전 이진 트리 : 마지막 레벨을 제외한 모든 노드가 차 있으며, 마지막 레벨의 노드는 전부 차 있지 않아도 되지만 왼쪽은 반드시 채워져 있어야 한다.

단순 탐색 : 최대 n번의 탐색
이진 탐색 : 최대 log n번의 탐색

---

Binary Search Tree

모든 왼쪽 자식들은 루트와 부모보다 작은 값이고, 모든 오른쪽 자식들은 루트와 부모보다 큰 값을 가지고 있는 형태를 이진 탐색트리 (Binary Search Tree) 라고 한다.

---

Tree traversal

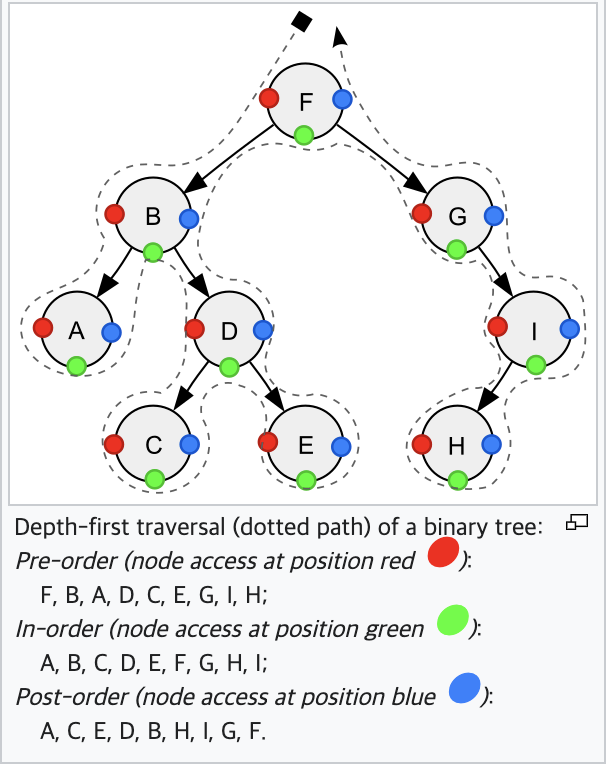
• pre-order (전위 순회)
  루트를 시작으로 왼쪽 노드들을 탐색한 후, 오른쪽 노드 탐색
• in-order (중위 순회)
  루트를 가운데 두고 왼쪽부터 탐색 -> 루트 -> 오른쪽 탐색
• post-order (후위 순회)
  왼쪽 끝 노드부터 탐색하며 루트를 거치지 않고 오른쪽 탐색 후, 마지막에 루트 탐색

---

Reference

Tree traversal

Tree traversal img : wiki