[세상에서 가장 쉬운 통계학 입문] 을 읽고 -표본평균을 이용한 모평균의 구간추정

---

표본평균을 이용한 모평균의 구간추정

: 모분산을 알고 있는 정규모집단의 모평균은?

1.모평균이나 모분산을 추정하기 위한 방법

• 특정의 불확실한 현상의 본질을 알고 싶을 경우,
  정규모집단의 모평균 또는 모표준편차를 추정함으로써 그것을 대신할 수 있다

• '모분산을 알고 있는 정규모집단'에 대해서 그 모평균을 구간추정하는 방법

  1.대량으로 데이터를 모으면, 모집단이 어떤 분포고,그 표본평균은 정규분포에 가까워진다는 성질을 이용하는 방법 (중심극한정리)=> 대표본 추정

  2.분포에 대한 지식을 가정하지 않는 비모수적이라는 방법을 이용

  3.정규모집단이라는 것은 알지만,모평균과 모분산을 모를 때의 추정

2.표본평균을 이용한 모평균의 구간추정

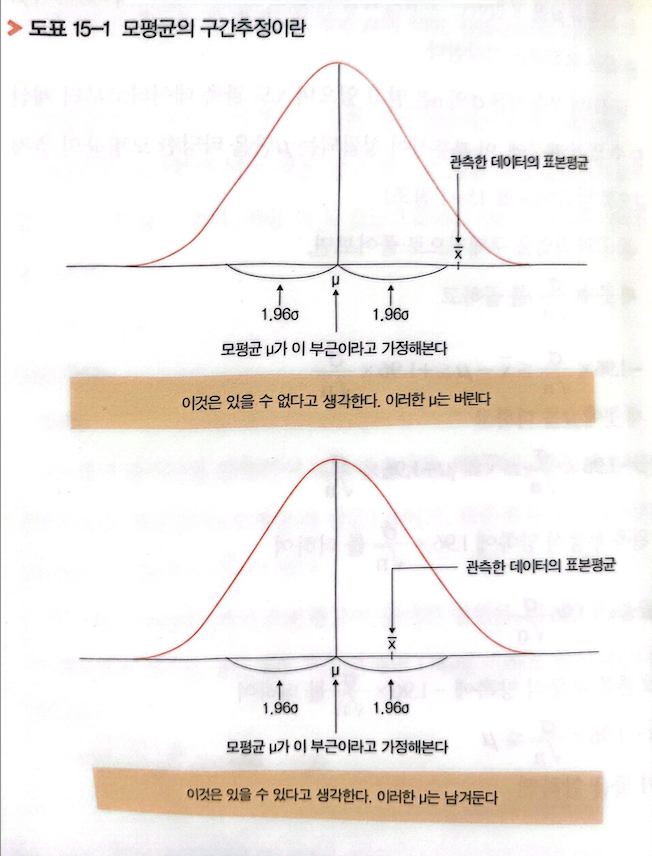
• 정규모집단에서 모표준편차가 $\sigma$ (모분산이 $\sigma$$^2$)라는 사실을 알고 있을 경우,
  모평균 $\mu$를 n개의 표본에서 추정하기 위해서는 표본평균 $\bar{x}$ 를 계산하여
  -1.96 $\leq$$\frac{\bar{x}-\mu}{\frac{\sigma}{\sqrt{n}}}$ $\leq$ +1.96을 만족시키는 $\mu$ 기각하지 않고 남기면 된다.

이때, $\mu$의 95% 신뢰구간은
$\bar{x}$-1.96$\frac{\sigma}{\sqrt{n}}$ $\leq$ $\mu$ $\leq$$\bar{x}$+1.96$\frac{\sigma}{\sqrt{n}}$

---