머신러닝 알고리즘 정리

선형 회귀

종속 변수 y와 한 개 이상의 독립 변수 x와의 선형 상관 관계를 모델링하는 회귀 분석 기법.

sklerarn.linear_model.LinearRegression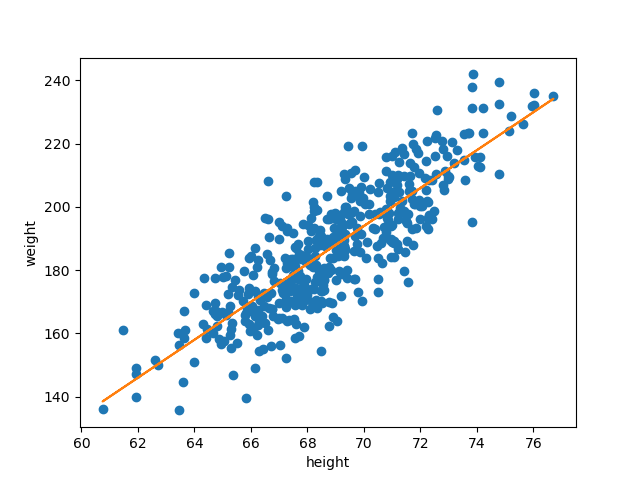

주요 파라미터

• fit_intercept :(T/F) 이 모델에 대한 절편을 계산할지에 대한 여부. False로 설정하면 계산에 절편이 사용되지 않음.(데이터가 중앙에 위치할 것으로 예상)
• n_jobs : 계산에 사용할 코어 갯수

특징

1. 다른 모델들에 비해 간단한 작동 원리
2. 학습 속도가 빠름
3. 하이퍼파라미터 갯수가 적음
4. 이상치에 영향을 크게 받음.
5. 데이터가 수치형 변수로만 이루어져 있을 경우, 데이터의 경향성이 뚜렷할 경우 사용하기 좋음.

결정 트리

종속 변수 y와 한 개 이상의 독립 변수 x와의 선형 상관 관계를 모델링하는 회귀 분석 기법.

sklerarn.tree.DecisionTreeRegressor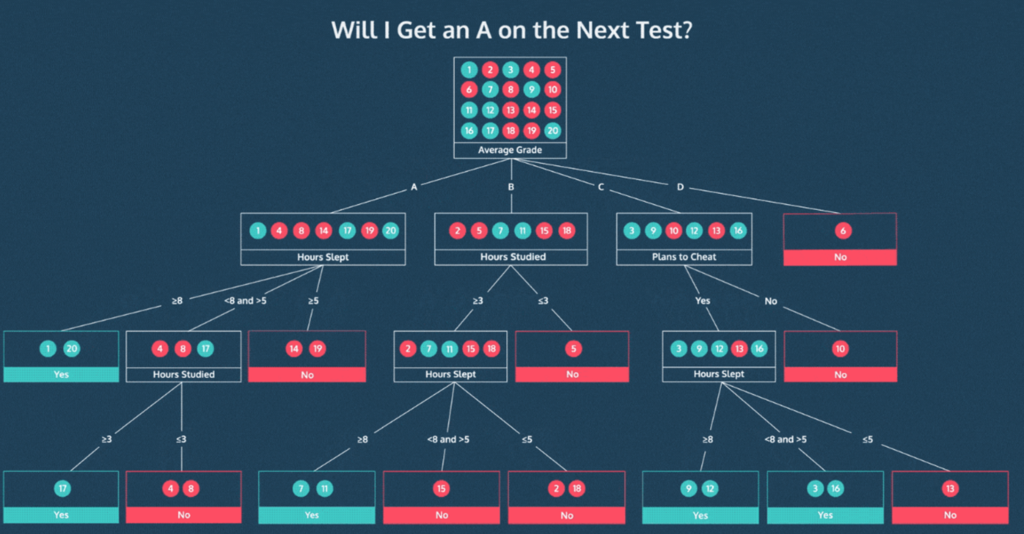

주요 파라미터

• criterion : {gini/entropy} 가지 분할의 품질 측정 기준
• max_depth : 트리의 최대 깊이
• min_samples_split : 내부 노드를 분할하는 데 필요한 최소 샘플 수
• min_samples_leaf : 리프 노드에 있어야 하는 최소 샘플 수
• max_leaf_nodes : 리프 노드 숫자의 제한치

특징

1. 결과를 해석하고 이해하기 쉬움 (직관적)
2. 자료를 가공할 필요가 없음 (정규화하거나, 파생변수를 생성하지 않아도 됨)
3. 수치 자료와 범주 자료 모두에 적용할 수 있음.
4. 화이트박스 모델, 시각화 가능
5. 안정적(해당 모델 추리의 기반이 되는 명제가 손상되었더라도 잘 동작)
6. 대규모의 데이터 셋에서도 잘 동작 (데이터의 스케일에 구애받지 않음. 각 특성이 개별적으로 처리됨)

앙상블 기법

여러 모델들을 엮어 더 좋은 모델을 만드는 방법

• 랜덤 포레스트
  - 디시전 트리는 각각의 트리들은 예측을 잘 할 수 있을 지 모르나, train 데이터셋에 과대적합 될 수 있음.
  • 예측을 잘 하지만 서로 다른 부분에 과대적합 된 트리들의 평균을 채택
• 그래디언트 부스팅 트리
  - 랜덤 포레스트는 서로 다른 트리의 묶음이라면, 그래디언트 부스팅 트리는 순차적으로 결정 트리를 만들어 이전 트리의 오차를 보완
  • 얕은 트리를 많이 연결하여 성능이 좋은 최종 모델을 생성

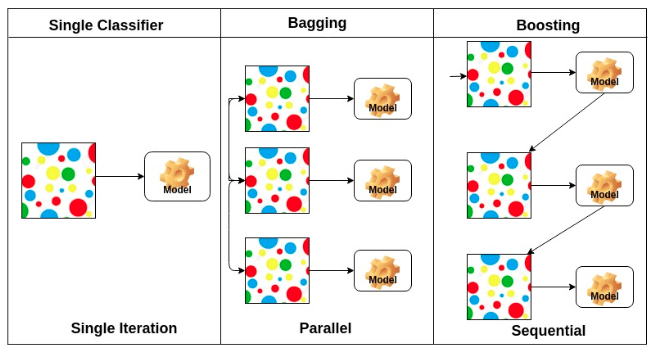
Bagging vs Boosting

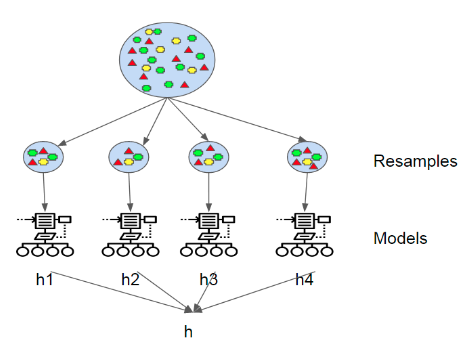
Bagging (Bootstrap Aggregating)

• 부트스트랩을 통해 조금씩 다른 훈련 데이터에 대해서 훈련된 기초 분류기(base learner)들을 결합(aggregating)하는 방법.

  • 여러개의 모델이 독립적(서로 영향을 받지 않음).

  • 여러개의 모델을 만들기 위해 각 모델 별로 임의의 데이터 세트를 생성하는데, 이 때 중복을 허용하여 무작위로 N개를 선택하여 데이터 세트를 선택함. => 부트스트랩 방식

  • 하나의 트리는 작은 편향과 큰 분산을 갖기 때문에 하나의 깊은 트리는 과적합되기 쉽다. 부트스트랩은 편향은 그대로 유지하면서 분산은 감소시키기 때문에 포레스트의 성능을 향상시킨다.

    

Random Forest

sklerarn.ensemble.RandomForestRegressor

주요 파라미터

• criterion : {gini/entropy} 가지 분할의 품질 측정 기준
• max_depth : 트리의 최대 깊이
• min_samples_split : 내부 노드를 분할하는 데 필요한 최소 샘플 수
• n_estimators : 트리의 개수를 결정
• max_leaf_nodes : 리프 노드 숫자의 제한치

특징

1. 성능이 뛰어남. 매개변수 튜닝을 많이 필요로 하지 않음.
2. 결정 트리와 달리 시각화 불가능.
3. 데이터의 크기가 커지면 시간이 오래 걸림.
4. 차원이 높고 희소한 데이터에는 잘 작동하지 않을 수 있음.

Extra Tree

sklerarn.ensemble.ExtreTreesRegressor

주요 파라미터

• criterion : {gini/entropy} 가지 분할의 품질 측정 기준
• max_depth : 트리의 최대 깊이
• min_samples_split : 내부 노드를 분할하는 데 필요한 최소 샘플 수
• n_estimators : 트리의 개수를 결정
• max_features : 최상의 분할을 찾을 때 고려해야 할 기능의 수

특징

1. 분기 지점을 랜덤으로 선택, 랜덤 포레스트보다 속도가 더 빠름
2. 더 많은 특성을 고려할 수 있음.
3. 데이터의 크기가 커지면 시간이 오래 걸림.
4. 차원이 높고 희소한 데이터에는 잘 작동하지 않을 수 있음.

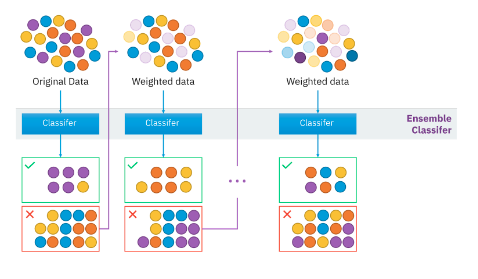
Boosting

• 여러 얕은 트리를 연결하여 편향과 분산을 줄여 강력한 트리를 생성하는 기법. 이전 트리에서 틀렸던 부분에 가중치를 주며 지속적으로 학습.
  

=

GBM(Gradient Boosting Tree)

sklerarn.ensemble.GradientBoostingRegressor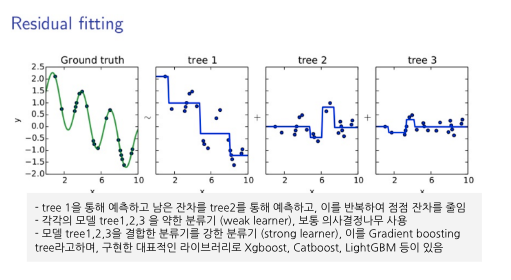

주요 파라미터

• loss : {'squaread_error','absiolute_error','huber','quantile'}최적화시킬 손실 함수
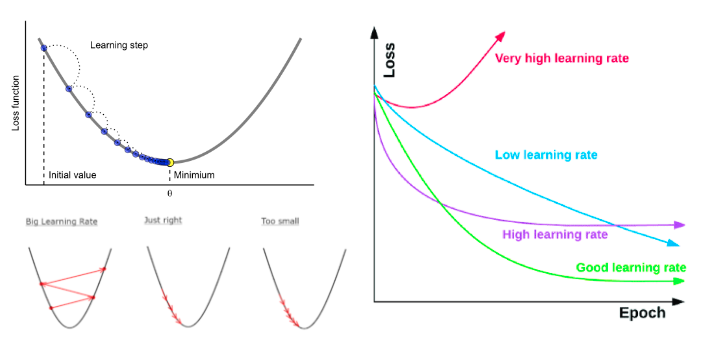
• learning_rate : 각 트리의 기여도를 제한
• n_estimators : 부스팅 단계를 결정
• subsample : 개별 기본 학습자를 맞추는 데 사용할 샘플의 비율

특징

1. 랜덤포레스트와 달리 무작위성이 없음.
2. 매개변수를 조정하는 것이 중요하고 훈련 시간이 긺.
3. 데이터의 스케일에 구애받지 않음.
4. 고차원의 희소한 데이터에 잘 작동하지 않음.