CNN -(2)

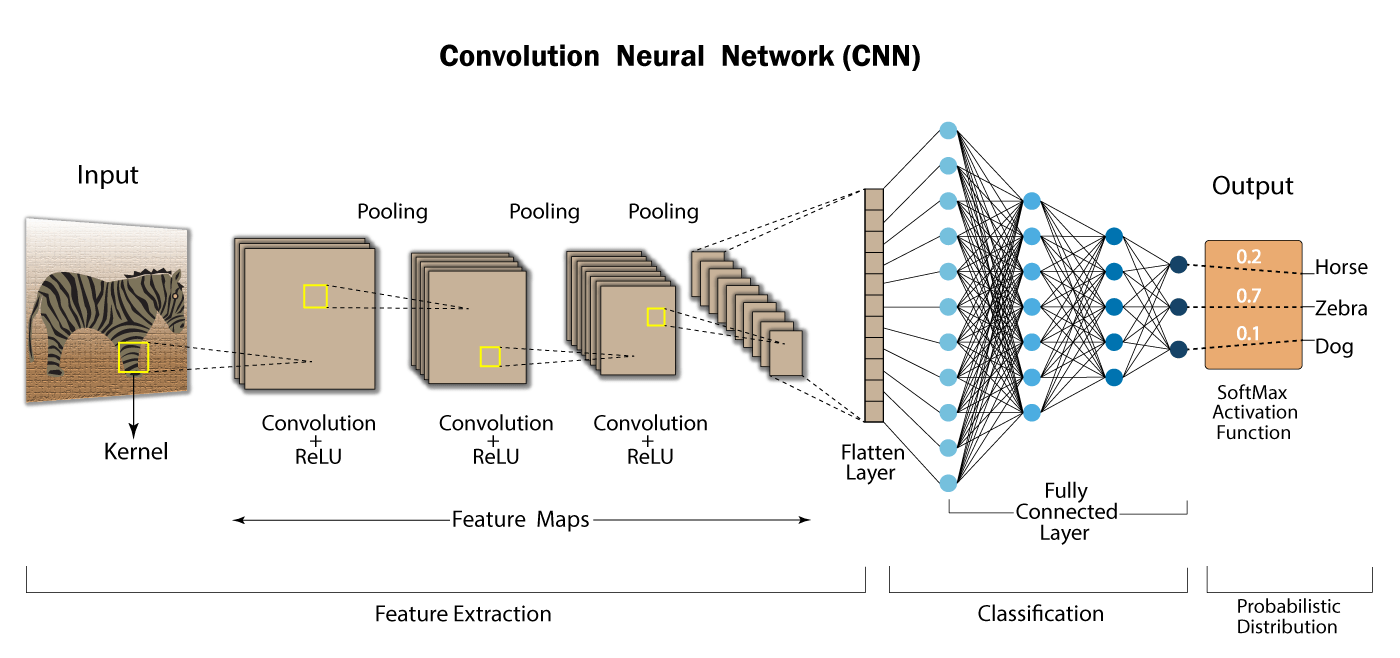
우선 합성곱 신경망은 DNN과는 다른 점이 있다.
바로 2차원 이미지 그대로를 이용하기 때문에 flatten을 이용하지 않아도 된다는 것! 그러나 대신 입력 이미지는 항상 깊이(채널) 차원이 있어야 한다. Conv2D 층을 사용하기 위해서 마지막에 이 채널 차원을 추가해야 한다.

from tensorflow import keras
from sklearn.model_selection import train_test_split

(train_input, train_target), (test_input, test_target) = \
    keras.datasets.fashion_mnist.load_data()

train_scaled = train_input.reshape(-1, 28, 28, 1) / 255.0

train_scaled, val_scaled, train_target, val_target = train_test_split(
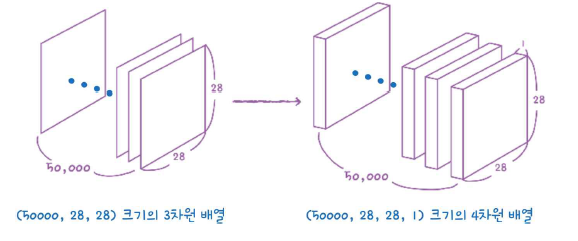
    train_scaled, train_target, test_size=0.2, random_state=42)

이렇게 원래 (48000, 28, 28)크기인 train_input이 (48000, 28, 28, 1)인 train_scaled가 되었다.

합성곱 신경망 만들기

전형적인 합성곱 신경망의 구조는

1. 합성곡 층으로 이미지에서 특징을 감지한 후
2. 밀집층으로 클래스에 따른 분류 확률을 계산한다.

코드로 구현해 보면,

model=keras.Sequential()
model.add(keras.layers.Conv2D(32,kernel_size=3,activation='relu',padding='same',input_shape=(28,28,1)))

우선 Sequential 클래스의 객체를 만들고 첫 번째 합성곱 층인 Conv2D를 추가한다.

1. 이 합성곱 층은 32개의 필터를 사용한다.
2. 커널의 크기는 (3,3)이다.
3. 렐루 함수를 활성화 함수로 사용한다.
4. 패딩은 세임 패딩이다.
5. input shape는 (28, 28, 1)이다.

그 다음엔 풀링 층을 추가한다. 전형적인 풀링 크기인 (2,2)로 지정한다. Max pooling을 사용한다.

model.add(keras.layers.MaxPooling2D(2))

세임 패딩을 적용했기 때문에 합성곱 층에서 출력된 특성 맵의 가로세로 크기는 입력과 동일하다. 그 다음 (2, 2) 풀링을 적용했으므로 특성 맵의 크기는 절반으로 줄어든다. 또 합성곱 층에서 32개의 필터를 사용했기 때문에 이 특성 맵의 깊이는 32가 된다. 그래서 최종적으로 첫 번째 특성 맵의 크기는
(14, 14, 32)가 될 것이다.

그럼 이제 두 번째 합성곱-풀링 층을 추가해 보자. 이번에는 필터의 갯수를 64로 늘려 보자.

model.add(keras.layers.Conv2D(64,kernel_size=3,activation='relu',padding='same'))
model.add(keras.layers.MaxPool2D(2))

이 층 역시 세임 패딩을 사용한다. 즉, 입력의 가로세로 크기를 줄이지 않는다. 그러나 풀링 층에서 절반으로 줄인다. 64개의 필터를 사용했으므로 여길 거쳐서 만들어지는 특성 맵의 크기는 (7, 7, 64)가 될 것이다.

이제 3차원 특성 맵을 일렬로 펼칠 차례다. 왜냐하면 마지막에 10개의 뉴런을 가진 (밀집) 출력 층에서 확률을 계산하기 때문이다. 여기서는 출력층 전에, Flatten층 뒤에 층을 하나 더 둘 것이다.

즉 Flatten - Dense - 출력 이런 식이다.

model.add(keras.layers.Flatten())
model.add(keras.layers.Dense(100, activation='relu'))
model.add(keras.layers.Dropout(0.4))
model.add(keras.layers.Dense(10, activation='softmax'))

그리고 과대적합을 막기 위해 드롭아웃 층도 챙겨 넣어주었다. 요약을 보자!

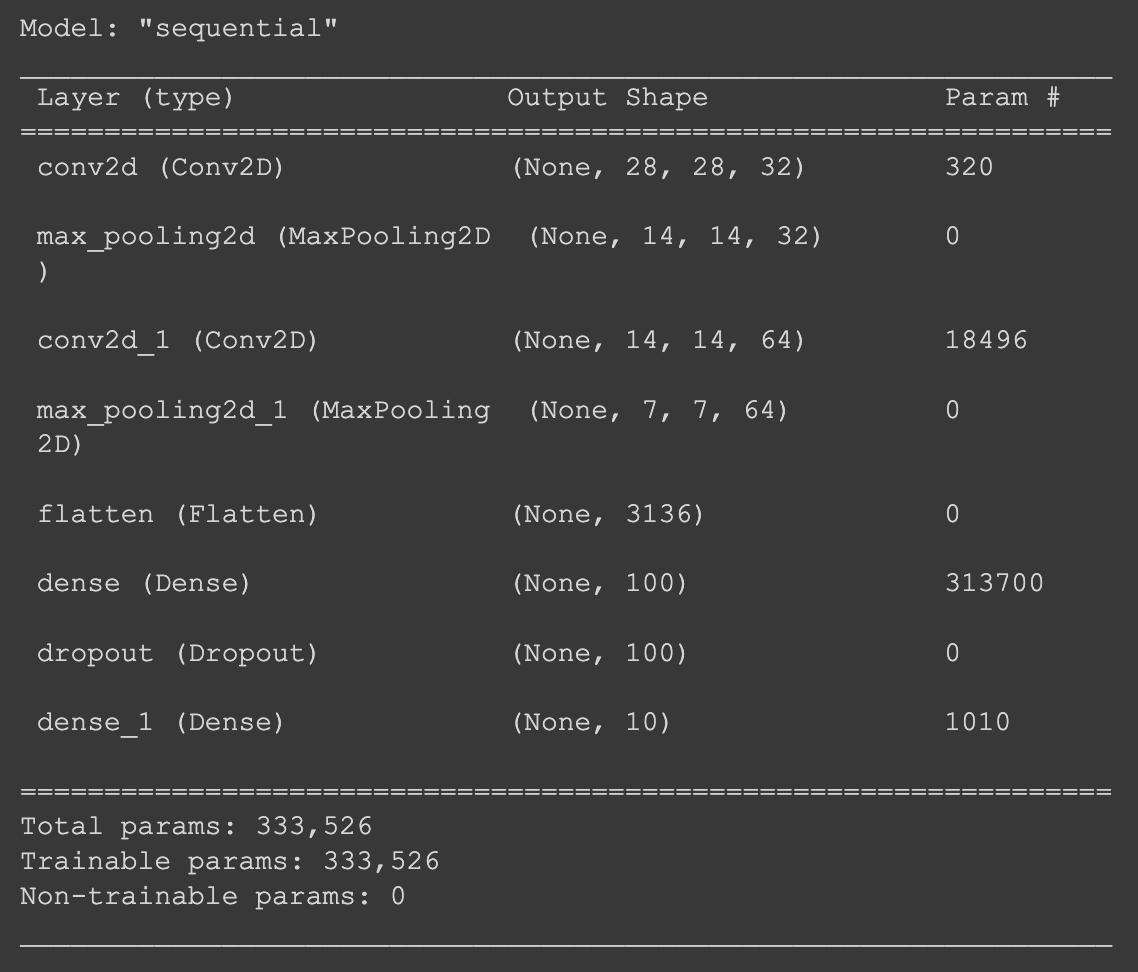
요약을 보면, 첫 번째 합성곱 층을 통과하면서 특성 맵의 깊이는 32가 되고 두 번째 합성곱 층에서 층의 깊이가 64로 늘어난다. 번면 특성 맵의 가로세로 크기는 풀링 층에서 반으로 줄어든다.

그리고 파라미터 계산을 보면, 첫 번째 층은 (3, 3)짜리 필터를 사용했었고, 깊이가 1이었다. 또 필터마다 하나의 절편이 있다. 그러므로,
즉, 3 X 3 X 1 X 32 + 32 = 320

(필터의 크기 X 원래 깊이 X 추가한 필터 갯수 + 필터 갯수만큼의 절편)

두번째 합성곱 층은 64개의 필터를 사용했고, 원래 깊이는 32이다. (위에서 32개의 필터를 사용했었으니까) 필터마다 하나의 절편이 있고, 크기는 (3, 3)이었다.

그래서, 3 X 3 X 32 X 64 + 64 = 18496이 된다.

Flatten 클래스에서는 (7, 7, 64) 크기의 특성 맵을 1차원 배열로 펼치면 3136크기의 배열이 된다. (7 X 7 X 64) 이를 100개의 뉴런과 완전 열결해야 하므로 3136 X 100 + 100 = 313,700개의 파라미터가 생긴다.

마찬가지 방식으로 계산을 하면 마지막 출력층의 모델 파라미터 갯수는 1,010개가 된다. (100 X 10 + 10).

keras는 층의 구성을 그림으로 표현해주는 plot_model()함수도 지원한다.

keras.utils.plot_model(model, show_shapes=True)

이 그래프를 아예 그림으로 그려보면 다음과 같다.

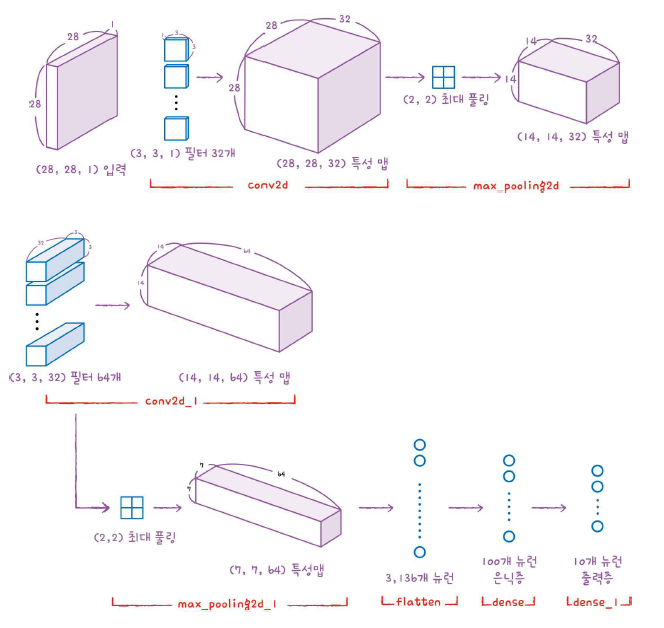
이제 모델 컴파일을 하자!

model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', 
              metrics='accuracy')

checkpoint_cb = keras.callbacks.ModelCheckpoint('best-cnn-model.h5', 
                                                save_best_only=True)
early_stopping_cb = keras.callbacks.EarlyStopping(patience=2,
                                                  restore_best_weights=True)

history = model.fit(train_scaled, train_target, epochs=20,
                    validation_data=(val_scaled, val_target),
                    callbacks=[checkpoint_cb, early_stopping_cb])

모델 체크포인트 콜백과 EarlyStopping 콜백도 해 보았다.

plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.xlabel('epoch')
plt.ylabel('loss')
plt.legend(['train', 'val'])
plt.show()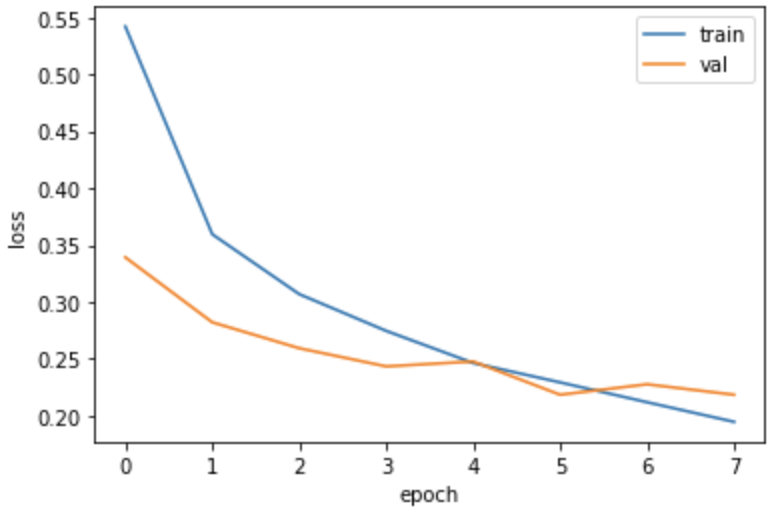

model.evaluate(val_scaled, val_target)

성능을 확인해 보면,

이건 이제 6번째, index 5의 출력과 같은 결과다.

이제 새로운 이미지를 넣어 테스트해 보면, (편의상 검증 세트의 첫 번째 샘플을 새로운 이미지라고 가정해서 넣어 보자)

plt.imshow(val_scaled[0].reshape(28, 28), cmap='gray_r')
plt.show()

맷플롯립에서는 흑백 이미지에 깊이 차원은 없으니 (28,28,1)을 (28, 28)로 바꾸어주었다.(데이터를 보려고)

핸드백인 것 같다.

이제 이걸 모델에 넣고 그래프를 그려 보면,

preds = model.predict(val_scaled[0:1])
plt.bar(range(1, 11), preds[0])
plt.xlabel('class')
plt.ylabel('prob.')
plt.show()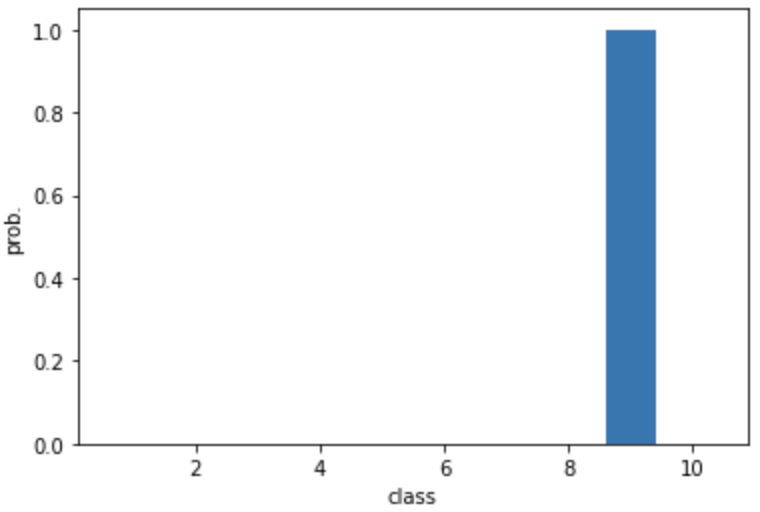

9라고 굉장히 강력하게 주장하고 있다. (다른 건 0에 가깝고, 9만 엄청 확률값이 높다)
실제로 결과 값을 프린트해보면 (print(pred))

[[6.7846774e-12 8.1426743e-22 8.9696543e-16 7.7117090e-15 6.6757140e-14
  1.4335832e-13 3.7601382e-14 3.6749163e-12 1.0000000e+00 1.8052020e-13]]

9만 1이고 나머지는 0에 가까운 걸 확인해볼 수 있다.

아까 9 여기서 한글 레이블로 뭐였는지 보면,

classes = ['티셔츠', '바지', '스웨터', '드레스', '코트',
           '샌달', '셔츠', '스니커즈', '가방', '앵클 부츠']

다음과 같았다.

import numpy as np
print(classes[np.argmax(preds)])

이렇게 해보면,

"가방" 이 프린트된다!

잘 예측하는 것 같다.

마지막으로 맨 처음에 떼어 놓았던 테스트 세트로 이 신경망의 일반화 가능성, 즉 random input에 대한 성능을 가늠해 보자.

훈련 세트와 검증 세트에서 했던 것처럼 픽셀값의 범위를 0~1 사이로 바꾸고 이미지 크기를 (28, 28)에서 (28, 28, 1)로 바꾼다.

test_scaled = test_input.reshape(-1, 28, 28, 1) / 255.0

그다음 evaluate 해보면

model.evaluate(test_scaled, test_target)

[0.24227263033390045, 0.9156000018119812]

91% 정도가 나온다. 검증 세트보다 약간 작긴 하지만 과적합인 정도는 아니다.

끝!