5장 정리
머신러닝의 기본 요소
5.1 일반화 : 머신러닝의 목표
5.2 머신 러닝 모델평가
5.3 훈련 성능 향상하기
5.4 일반화 성능 향상하기
5.5 요약
핵심 내용
- 머신러닝의 근본 문제인 일반화와 최적화 사이의 긴장 관계 이해하기
- 머신러닝 모델의 평가 방법
- 훈련 성능 향상을 위한 모범 사례
- 일반화 성능 향상을 위한 모범 사례
이 장에서는 정확한 모델 평가의 중요성 및 훈련 과 일반화 사이의 균형을 강조하면서 머신러닝에 대한 새로운 직관을 확고한 개념으로 정립하겠습니다.
5.1 일반화 : 머신러닝의 목표
- 머신러닝의 근본적인 이슈는 최적화와 일반화 사이의 줄다리기 입니다.
- 최적화 : 가능한 훈련 데이터에서 최고의 성능을 얻으려고 모델을 조정하는 과정입니다.
- 일반화 : 훈련된 모델이 이전에 본 적 없는 데이터에서 얼마나 잘 수행되는지 의미합니다.
- 당연히 목표는 좋은 일반화 성능을 얻는 것.
5.1.1 과소 적합과 과대적합 p180~186
- 훈련 데이터의 손실이 낮아질수록 테스트 데이터의 손실도 낮아진다.
- 일반화 성능이 더 이상 높아지지 않으며 검증 세트의 성능이 멈추고 감소되기 시작한다. = (과대적합)
- 이는 훈련 데이터에 특화된 패턴을 학습하기 시작했다는 의미이다.
- 과대적합하는 3가지 이유
- 데이터에 잡음 있음 -> 데이터 자체의 잘못
- 불확실성 존재 -> 데이터의 성질 자체가 애매함
- 드문 특성이 포함됨 -> 가짜 상관관계
기존 데이터의 784차원에 백색 잡음인 784개 의 차원을 연결하여 새로운 훈련 세트를 만듭니다. 따라서 데이터의 절반은 잡음입니다. 비교를 위해 모두 0인 784개의 차원을 연결하여 동일한 데이터셋을 만듭니다. 의미 없는 특성의 연결은 데이터의 기존 정보에 전혀 영향을 미치지 않습니다.
즉, 무언가 추가만 한 것입니다. 사람의 분류 정확도는 이런 변환에 전혀 영향을 받지 않습니다.
# 5-1) MNIST에 백색 잡음 픽셀과 0 픽셀을 추가하기
from tensorflow.keras.datasets import mnist
import numpy as np
(train_images, train_labels), _ = mnist.load_data()
train_images = train_images.reshape((60000, 28 * 28))
train_images = train_images.astype("float32") / 255
train_images_with_noise_channels = np.concatenate(
[train_images, np.random.random((len(train_images), 784))], axis=1)
train_images_with_zeros_channels = np.concatenate(
[train_images, np.zeros((len(train_images), 784))], axis=1)이 두 훈련 세트에서 2장의 모델을 훈련해 보겠다.
# 5-2) 백색 잡음과 0을 추가한 MNIST 데이터에서 모델 훈련하기
from tensorflow import keras
from tensorflow.keras import layers
def get_model():
model = keras.Sequential([
layers.Dense(512, activation="relu"),
layers.Dense(10, activation="softmax")
])
model.compile(optimizer="rmsprop",
loss="sparse_categorical_crossentropy",
metrics=["accuracy"])
return model
model = get_model()
history_noise = model.fit(
train_images_with_noise_channels, train_labels,
epochs=10,
batch_size=128,
validation_split=0.2)
model = get_model()
history_zeros = model.fit(
train_images_with_zeros_channels, train_labels,
epochs=10,
batch_size=128,
validation_split=0.2)시간에 따라 각 모델의 검증 정확도가 어떻게 변화하는지 비교해 보겠다.
# 5-3) 검증 정확도 비교 그래프 그리기
import matplotlib.pyplot as plt
val_acc_noise = history_noise.history["val_accuracy"]
val_acc_zeros = history_zeros.history["val_accuracy"]
epochs = range(1, 11)
plt.plot(epochs, val_acc_noise, "b-",
label="Validation accuracy with noise channels") #손실에서 더 값이 안좋게 나옴옴
plt.plot(epochs, val_acc_zeros, "b--",
label="Validation accuracy with zeros channels")
plt.title("Effect of noise channels on validation accuracy")
plt.xlabel("Epochs")
plt.ylabel("Accuracy")
plt.legend()
plt.show()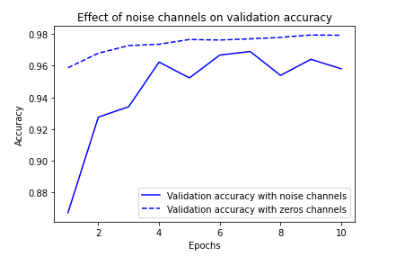
잡음 특성은 필연적으로 과대적합을 유발시킵니다.
따라서 특성이 모델에 유익한지 또는 모델을 혼란스럽게 만드는지 확실하지 않다면 훈련 전에 특성 선택을 수행하는 것이 일반적입니다. 예를 들어 IMDB 데이터를 가장 자주 등장하는 최상위 1만 개 단어로 제한하는 것은 세련되지 않은 특성 선택 방법입니다.
즉, 특성과 레이블 사이의 상호 의존 정보 처럼 작업에 대해 특성이 얼마나 유익한지 측정합니다. 그 다음은 일정 임계 값을 넘긴 특성만 사용합니다. 이렇게 하면 앞선 예제에서 백색 잡음이 걸러질 수 있다.
5.1.2 딥러닝에서 일반화의 본질 p186
딥러닝 모델에 곤한 놀라운 사실은 표현 능력이 충분하다면 어떤 것에도 맞추도록 훈련할 수 있다는 것이다.
입력과 뒤섞은 레이블 사이에 아무런 관계가 없지만 비교적 작은 모델에서도 훈련 손실이 잘 감소합니다. 당연히 이런 상황에서 가능한 일반화가 없기 때문에 검증 손실은 시간이 지남에 따라 향상되지 않습니다.
# 5-4) 랜덤하게 섞은 레이블로 MNIST 모델 훈련하기
(train_images, train_labels), _ = mnist.load_data()
train_images = train_images.reshape((60000, 28 * 28))
train_images = train_images.astype("float32") / 255
random_train_labels = train_labels[:]
np.random.shuffle(random_train_labels)
model = keras.Sequential([
layers.Dense(512, activation="relu"),
layers.Dense(10, activation="softmax")
])
model.compile(optimizer="rmsprop",
loss="sparse_categorical_crossentropy",
metrics=["accuracy"])
model.fit(train_images, random_train_labels,
epochs=100,
batch_size=128,
validation_split=0.2)따라서 딥러닝 모델을 향상시키는 가장 좋은 방법은 더 좋고, 더 많은 데이터에서 훈련하는 것이라는 점을 항상 기억하세요.
5.2 머신 러닝 모델 평가 p193
이 절에서 머신 러닝 모델을 평가할 수 있는 여러 가지 방법을 소개합니다. 이 중 대부분은 이전 장에서 이미 보았습니다.
5.2.1 훈련, 검증, 테스트 세트 p193
모델 평가의 핵심은 가용한 데이터를 항상 훈련,검증,테스트 3개의 세트로 나누는 것입니다. 훈련 세트에서 모델을 훈련하고 검증세트에서 모델을 평가합니다. 모델을 출시할 준비가 되면 테스트 세트에서 최종적으로 딱 한번 모델을 테스트 합니다. 테스트 데이터는 가능한 제품 환경의 데이터와 비슷해야 합니다. 그 다음 모델을 제품환경에 배포합니다.
층이나 층의 유닛 개수를 선택합니다. (이런 파라미터를 네트워크의 가중치와 구분하기 위해 하이퍼파라미터라고 부릅니다.) 검증 세트에서 모델의 성능을 평가하여 이런 튜닝을 수행합니다.
본질적으로 이런 튜닝도 어떤 파라미터 공간에서 좋은 설정을 찾는 학습입니다.
셜국 검증 세트의 성능을 기반으로 모델의 설정을 튜닝하면 검증 세트로 모델을 직접 훈련하지 않더라도 빠르게 검증 세트에 과대적합될 수 있습니다.
이 현상의 핵심은 정보누설 개념이 있습니다. 검증세트의 모델 성능에 기반하여 모델의 하이퍼파라미터를 조정할 떄마다 검증 데이터에 관한 정보가 모델로 새는 것입니다.
하나의 파라미터에 개해 단 한 번만 튜닝한다면 아주 적은 정보가 누설됩니다. 한 번 튜닝하고 나서 검증 세트에 평가한 결과를 가지고 다시 모델을 평가할 만합니다.
데이터 훈련,검증,테스트 세트로 나누는 것은 간단해 보일 수 있지만 데이터가 적을 떄는 몇가지 고급 기법을 사용하면 도움이됩니다. 대표적으로
- 단순 홀드아웃 검증
- K-겹 교차 검증
- 셔플링을 사용한 K-겹 교차 검증
또한, 상식 수준의 기준 모델을 사용해서 훈련이 잘 진행되는지 확인하는 방법을 설명하겠다.
단순 홀드아웃 검증 p194
데이터의 일정량을 테스트 세트로 뗴어 놓습니다. 남은 데이터에서 훈련하고 테스트 세트로 평가합니다. 앞 절에서 설명했듯이 정보 누설을 막기 위해 테스트 세트를 사용하여 모델을 튜닝해서는 안됩니다. 이런 이유로 검증 세트도 따로 떼어 놓아야 합니다.
평가 방법은 단순해서 한가지 단점이 있다. 데이터가 적을 떄는 검증 세트와 테스트 세트의 샘플이 너무 적어 주어진 전체 데이터를 통계적으로 대표하지 못할 수 있습니다. 쉽게 이를 확인할 수 있습니다. 다른 난수 초깃값으로 셔플링해서 데이터를 나누었을 때 모델의 성능이 매우 달라지면 바로 이 문제입니다. 다음에 이야기할 k-겹 교차 검증과 반복 k-겹 교차 검증이 이 문제를 해결할 수 있습니다.
K-겹 교차 검증
이 방식에서는 데이터를 동일한 크기를 가진 k개의 분할로 나눕니다. 각 분할 i에 대해 남은 k-1개의 분할로 모델을 훈련하고 분할 i에서 모델을 평가합니다. 최종 점수는 이렇게 얻은 k개의 점수를 평균합니다. 이 방법은 모델의 성능이 데이터 분할에 따라 편차가 클 때 도움이 됩니다. 홀드 아웃 검증처럼 이 방법은 모델의 튜닝에 별개의 검증 세트를 사용하게 됩니다.
셔플링을 사용한 반복 K-겹 교차 검증
이 방법은 비교적 가용 데이터가 적고 가능한 정확하게 모델을 평가하고자 할 때 사용합니다. 캐글 경연에서는 이 방법이 아주 크게 도움이 됩니다. 이 방법은 k-겹 교차 검증을 여러번 적용하되 k개의 분할로 나누기 전에 매번 데이터를 무작위로 섞습니다. 최종 점수는 모든 k-겹 교차 검증을 실행해서 얻은 점수의 평균이 됩니다. 결국 P*K개(P는 반복횟수)의 모델을 훈련하고 평가하므로 비용이 매우 많이 듭니다.
5.2.3 모델 평가에 대해 유념해야 할 점
평가 방식을 선택할 떄 다음 사항을 유의해야합니다.
- 대표성이 있는 데이터 : 일반적으로 훈련세트와 테스트 세트를 나누기전 데이터를 무작위로 섞는 것이 일반적입니다.
- 시간의 방향 : 모델이 사실상 미래 데이터에서 훈련될 것입니다. 이런 문제에서는 훈련 세트에 있는 데이터보다 테스트 세트에 있는 모든 데이터가 미래의 것이어야 합니다.
- 데이터 중복 : 한 데이터셋에 어떤 데이터 포인트가 두 번 등장하면 (실제 데이터셋에서 아주 흔한 일입니다.) 데이터를 섞고 훈련 세트와 검증 세트로 나누었을 때 훈련 세트와 검증 세트에 데이터 포인트가 중복될 수 있습니다. 이로 인해 훈련 데이터의 일부로 테스트하는 최악의 경우가 됩니다! 훈련 세트와 검증 세트가 중복되지 않는지 확인하세요.
5.3 훈련 성능 향상하기
최적적합 모델을 얻으려면 먼저 과대적합되어야 합니다. 따라서 문제를 다루기 시작할떄 초기 목표는 약간의 일반화 능력을 보이고 과대적합할 수 있는 모델을 얻는 것입니다. 이런 모델을 얻고 난 후 과대 적합과 싸워 일반화 성능을 개선하는 데 초점을 맞춥니다.
- 훈련되지 않습니다. : 시간이 지나도 훈련 손실이 줄어들지 않습니다.
- 훈련은 잘 시작되었지만 모델이 의미 있는 일반화르 달성하지 못합니다. : 상식 수준의 기분점을 넘어설 수 없습니다.
- 시간이 지남에 따라 훈련과 검증 손실이 모두 줄어들고 기준점을 넘어설 수 있지만 과대 적합되지 않을 것 같습니다. 여전히 과소적합 상태입니다.
이런 이슈를 해결하여 머신 러닝 프로젝트의 첫 번째 큰 이정표(상식 수준의 기준점을 넘을 수 있어 약간의 일반화 능력이 있고 과대적합하 수 있는 모델을 얻는 것)를 달성하는 방법을 알아보겠습니다.
5.3.1 경사 하강법의 핵심 파라미터 튜닝하기
항상 경사하강법 과정에 대한 설정에 문제가 있습니다. 옵티마이저 선택, 모델 가중치의 초깃값 분포, 학습률, 배치 크기입니다. 이 모든 파라미터는 상호 의존적 입니다.
일반적으로 나머지 파라미터는 고정하고 학습률과 배치 크기를 튜닝하는 것으로 충분합니다.
5.3.2 구조에 대해 더 나은 가정하기
모델이 훈련되지만 일반화 되지 않습니다. 아마 최악의 머신러닝 상황일것이다. 이는 접근 방식에 근본적으로 잘못된 무엇간가 있다는 의미이다. 먼저 단순하게 입력 데이터에 타깃 예측을 위한 정보가 충분하지 않을 수 있습니다.
또는 현재 사용하는 모델의 종류가 문제에 적합하지 않을 수 있습니다.
5.3.3 모델 용량 늘리기 p202
첫번째 모델을 과대적합 시켜야 한다.
훈련손실이 줄어들지 않는 문제와 마찬가지로 이런 문제는 항상 해결할 수 있다. 과대적합할 수 없는 것처럼 보인다면 모델의 표현능력이 부족한것이다. 용량이 더 큰 모델이 필요하다. 더 많은 정보를 저장할 수 있는 모델입니다. 층을 추가하거나(더 많은 가중치를 가지도록) 층 크기를 늘리거나, 현재 문제에 더 적합한 종류의 층(구조에 대해 더 나은 가정)을 사용할 수 있습니다.
5.4 일반화 성능 향상하기
모델이 어느 정도 일반화 성능을 갖조 과대적합할 수 있다면 이제 일반화를 극대화하는데 초점을 맞춤 차례입니다.
5.4.1 데이터셋 큐레이션
딥러닝의 일반화가 데이터의 잠재 구조에서 비롯된다는 것을 배웠습니다. 데이터를 사용하여 샘플 사이를 부드럽게 보간할 수 있다면 일반화 성능을 가진 딥러닝 모델을 훈련할 수 있을 것입니다. 주어진 문제에 지나치게 잡음이 많거나 리스트 정렬처럼 근본적으로 불연속적인 경우 딥러닝은 도움이 되지 않습니다. 딥러닝은 일종의 곡선을 맞추는 작업입니다.
따라서 적절한 데이터셋으로 작업하고 있는지 확인하는 것이 중요합니다.
- 데이터가 충분한지 확인해라. 데이터가 많을수록 좋은 모델이 만들어집니다.
- 레이블 할당 에러를 최소화합니다.
- 데이터를 정제하고 누락된 값을 처리합니다.
- 많은 특성 중에서 어떤 것이 유용한지 확실하지 않다면 특성 선택을 수행하세요.
데이터의 일반화 가능성을 향상시키는 매우 중요한 한 방법은 특성공학입니다. 대부분의 머신 러닝 문제에서 특성 공학은 성공을 위한 핵심 요소입니다.
5.4.2 특성공학
특성 공학은 데이터와 머신러닝 알고리즘(여기에서는 신경망)에 관한 지식을 사용하는 단계입니다. 모델에 데이터를 주입하기 전에 (학습이 아닌) 하드코딩된 변환을 적용하여 알고리즘이 더 잘 수행되도록 만들어 줍니다.
이해하기 위해서 쉬운 예를 하나 들겠다.
시계 이미지를 입력으로 받고 하루의 시간을 출력하는 모델을 개발한다고 가정합시다.
이미지의 원본 픽셀을 입력으로 사용한다면 어려운 머신러닝 문제가 될 것입니다. 이를 해결하려면 합성곱 신경망이 필요할 것이고 이 네트워크를 훈련하기 위해 많은 컴퓨팅 자원도 필요합니다.
고수준에서 이 문제를 이해하고 있다면 (우리는 시계에서 시간을 읽는 방법을 알고 있습니다.) 머신 러닝 알고리즘을 위해 훨씬 더 좋은 입력 특성을 만들 수 있습니다.
이것이 특성 공학의 핵심입니다. 특성을 더 간단한 방식으로 표현하여 문제를 쉽게 만듭니다.
딥러닝 이전에는 특성 공학이 먼신 러닝 워크플로에서 가장 중요한 부분이였습니다.
5.5 요약
- 머신러닝 모델의 목적은 이전에 본 적 없는 입력에서 정확하게 동작하는 일반화입니다. 이는 보기보다 어렵습니다.
- 심층 신경망은 훈련 샘플사이를 성공적으로 보간할 수 있는 모수 모델을 훈련하여 일반화를 달성합니다. 이런 모델은 훈련 데이터의 '잠재 매니폴드'를 학습 했다고 말할 수 있습니다. 이것이 딥러닝 모델이 훈련 도중 본 샘플에 매우 가까운 입력만 이해할 수 있는 이유입니다.
- 머신러닝의 근본적인 문제는 최적화 일반화 사이의 줄다리기 입니다. 일반화를 달성하기 위해 먼저 훈련 데이터를 잘 맞추어야 하지만 훈련 데이터에 대한 성능 향상은 잠시 후 불가피하게 일반화를 저해합니다. 딥러닝의 모든 모범 사례는 이런 긴장 관계를 관리하는 것입니다.
- 딥러닝 모델의 일반화 능력은 데이터의 잠재 매니폴드를 근사하는 방법을 학습하고 보간을 통해 새로운 입력을 이해할 수 있다는 사실에서 비롯됩니다.
- 모델을 개발하는 동안 모델의 일반화 능력을 정확하게 평가할 수 있어야 합니다. 간단한 홀드아웃 검증에서부터 k-겹 교차 검증과 셔플링을 사용한 반복 k-겹 교차 검증까지 다양한 평가 방법을 사용할 수 있습니다. 검증 데이터에서 모델로 정보가 누출될 수 있기 때문에 최종 모델평가를 위해 완전히 별개의 테스트 세트를 떼어 놓아야 한다는 것을 기억하세요.
- 모델을 구축하기 시작할 때 먼저 약간의 일반화 능력을 가지고 과대적합할 수 있는 모델을 만드는 것이 목표입니다. 이를 위한 모범 사례는 학습률과 배치 크기를 튜닝하고, 구조에 대해 더 나은 가정을 활용하고, 모델 용량을 늘리고 또는 단순히 더 오래 훈련하는 것입니다.
- 모델이 과대적합되기 시작할 때 규제를 통해 일반화 성능을 향상시키도록 목표가 바뀝니다.
이를 위해 모델 용량을 줄이고, 드롭아웃이나 가중치 규제를 추가하고 또는 조기 종료를 사용할 수 있습니다. 당연히 더 크고 더 좋은 데이터셋이 모델의 일반화를 향상시키는 데 언제나 가장 좋은 방법입니다.
