문제
지민이는 자신의 저택에서 MN개의 단위 정사각형으로 나누어져 있는 MN 크기의 보드를 찾았다. 어떤 정사각형은 검은색으로 칠해져 있고, 나머지는 흰색으로 칠해져 있다. 지민이는 이 보드를 잘라서 88 크기의 체스판으로 만들려고 한다.
체스판은 검은색과 흰색이 번갈아서 칠해져 있어야 한다. 구체적으로, 각 칸이 검은색과 흰색 중 하나로 색칠되어 있고, 변을 공유하는 두 개의 사각형은 다른 색으로 칠해져 있어야 한다. 따라서 이 정의를 따르면 체스판을 색칠하는 경우는 두 가지뿐이다. 하나는 맨 왼쪽 위 칸이 흰색인 경우, 하나는 검은색인 경우이다.
보드가 체스판처럼 칠해져 있다는 보장이 없어서, 지민이는 88 크기의 체스판으로 잘라낸 후에 몇 개의 정사각형을 다시 칠해야겠다고 생각했다. 당연히 88 크기는 아무데서나 골라도 된다. 지민이가 다시 칠해야 하는 정사각형의 최소 개수를 구하는 프로그램을 작성하시오.
내가 푼 방법
지민이는 보드를 잘라서 8x8 체스판을 만드려고 한다. 체스판 규칙은 우리가 아는 체스판. 흰 검이 번갈아 가면서 나타나야 한다.
그래서 다시 색칠해야 하는 사각형의 개수가 최소인 경우를 구하는 거다.
-
먼저, 입력받는 보드의 왼쪽 위 좌표가 (0,0), 오른쪽 아래 좌표가 (N,M).
즉 (y,x)처럼 받는거다. N줄에 M개의 색이 있는 것이다.(문제가 N을 줄로 받기 때문에 그에 맞추자.)
-
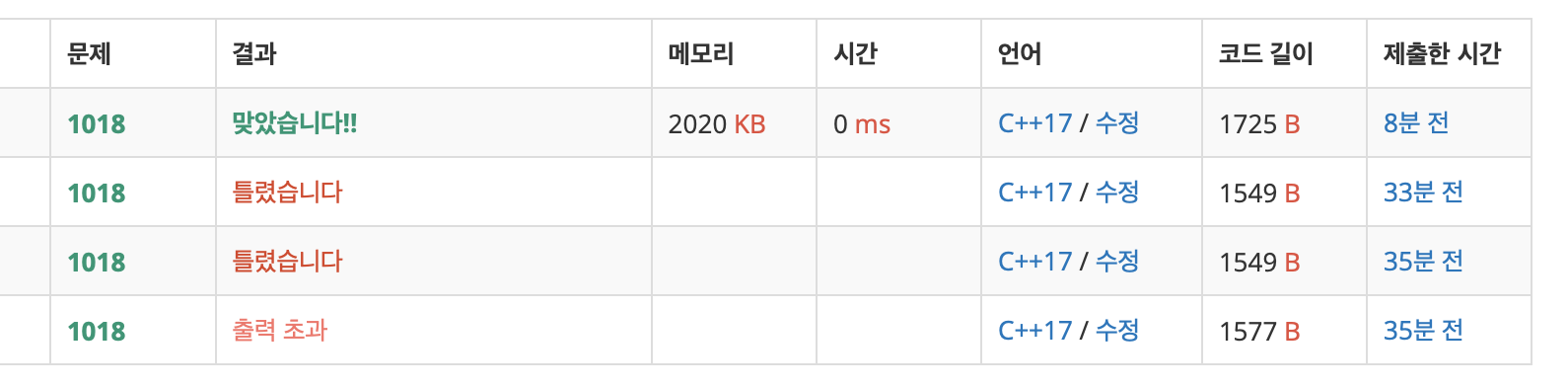
내가 이 문제를 잘못 읽어서 제일 시간 낭비를 한 구간인데, 정의가 맨 왼쪽 위가 검은색이거나 흰 색인 경우지, 우리가 값을 구할 때 기준이 맨 왼쪽위가 아니라는 거다. 나는 이걸 맨 왼쪽 위가 기준인줄 알고 뒀다가 틀렸습니다가 3번이나 떳다.
-
우리가 판단해야 하는 체스판의 크기는 8 x 8 로 고정되어 있으므로, 보드가 맨 왼쪽 위부터 맨 오른쪽 아래 까지 고정된 크기로 잘렸을 때의 값을 구해주면 될 것 같다는 생각이 들었다. 체스판의 크기가 고정되어 있는 것이 이 문제를 엄청 쉽게 만들어 준 것 같다.
내 코드
#include <iostream>
#define FASTIO ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
int N,M;
char board[51][51];
int checkboard(char sletter, int sy, int sx){
int a_min_n = 0;
int b_min_n = 0;
for(int i = 0; i<8; i++)
for(int j = 0; j<8; j++){
if( (i+j) % 2 == 0 ) { // 합이 짝수면 시작점과 글자가 같아야 한다.
if (board[sy + i][sx + j] != sletter) {
a_min_n += 1;
}
else
b_min_n += 1;
}
else if( (i+j) % 2 == 1) {
if (board[sy + i][sx + j] == sletter) {
a_min_n += 1;
}
else
b_min_n += 1;
}
}
return a_min_n > b_min_n ? b_min_n : a_min_n;
}
int main(){
cin >> N >> M;
char sletter = ' ';
int answer = 66; // 8*8 이므로 64개를 넘을 수 없음.
int k;
for (int i = 0; i<N; i++)
for (int j = 0; j<M; j++)
cin >> board[i][j]; // 보드 입력 마침.
for (int i = 0; i<N-7; i++)
for (int j = 0; j<M-7; j++) {
sletter = board[i][j]; // 이 글자와 좌표를 기준으로 오른쪽 8칸, 아래 8칸 검사.
k = checkboard(sletter,i,j);
if (answer > k)
answer = k;
}
cout << answer;
}하.. 왼쪽 위가 기준이라는 걸로 생각해서 시간을 너무 많이 썼다. 문제 자체는 굉장히 쉬웠다.