6자유도(6DOF) 비행체
(X,Y,Z) 축으로 이동하고, (X,Y,Z) 축으로 회전도 하는 비행체를 구현하기 위해 마우스를 위로 올렸을 때 비행체의 Y 축(Pitch 축)을 기준으로 회전을 하도록 만들었는데
(마우스 좌/우 - Z 축(Yaw 축))
(마우스 위/아래 - Y 축(Pitch 축))
(Q/E - X 축(Roll 축))
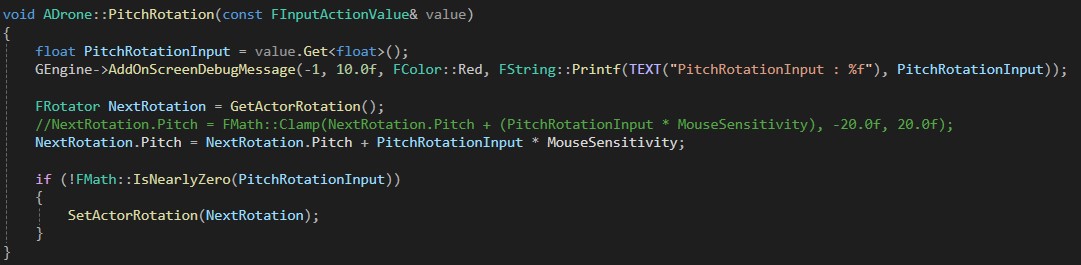
실행했을 때 최대 90도 ~ 최저 -90도까지만 돌아가고 더 이상 돌아가지 않았다.
이 문제를 해결하기 위해 SetActorRotation() 대신에 AddActorLocalRotation()을 사용하니 Y축 기준 360도 회전에 문제가 없었다.
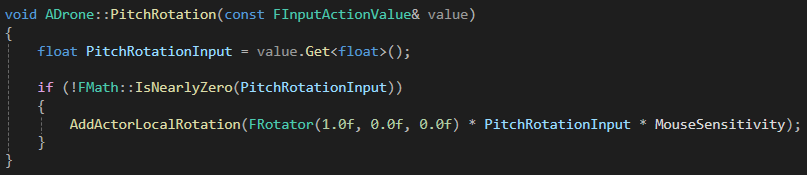
하지만, (Z,X)축에 대해선 SetActorRotation()을 쓰고 Y 축에 대해서는 AddActorLocalRotation()을 사용하니 X 축(Roll 축)을 기준으로 비행체를 90도 돌리고나서 마우스를 위/아래, 좌/우로 움직였을 때 비행체가 같은 축으로 회전을 하였다 => Gimbal Lock 발생
Gimbal Lock에 대해 찾아보다보니 SetActorRotation()과 AddActorLocalRotation()을 같이 쓴 것이 원인이였다.
-
SetActorRotation(): 월드 좌표계 기준으로 회전을 적용- 월드 좌표계에서는 X/Y/Z 축이 Gimbal처럼 동작
- Z → Y → X 순으로 영향을 줌
- Z 축으로 회전하는 것은 Y 축, X 축에도 영향을 줌
- Y 축으로 회전하는 것은 X 축에도 영향을 줌
- X 축으로 회전하는 것은 다른 축에 영향을 주지 않음

-
AddActorLocalRotation(): 액터의 로컬 좌표계를 기준으로 회전을 적용- 로컬 좌표계에서는 한 축이 회전할 때마다 다른 축들도 함께 회전
- 어느 축으로 회전을 하든 안하든, 모든 축이 서로 수직을 이룸 => 특정 축이 다른 축에 완전히 겹치는 일이 발생하지 않음
(Z,X) 축에 대해선 SetActorRotation()을 사용하고 Y 축에 대해서는 AddActorLocalRotation()을 사용하면 Z 축(Yaw 축)으로 회전했을 때는 (X,Y) 축에 동시에 영향(같이 회전)을 주기 때문에 상관 없지만, Y 축으로 90도 회전하게 되면 X 축에만 영향을 주고 X 축이 Z 축과 같아져서 두 축이 한 축처럼 같은 동작을 하게 되는 것이었다 => Gimbal Lock 발생(위에서 X 축(Roll 축)을 회전시켜 발생한 Gimbal Lock은 월드 좌표계(Z 축)와 로컬 좌표계(Y 축)를 섞어 사용해서 축이 겹친 것처럼 보인 것)
(X,Y,Z) 축 전부 회전할 때 AddActorLocalRotation()을 사용하도록 변경하니, 6자유도 전부 잘 작동하였다
Gimbal Lock
Gimbal
https://en.wikipedia.org/wiki/Gimbal_lock
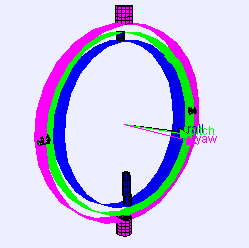
위의 위키피디아 링크를 들어가보면 그림과 같은 고리가 회전하는 걸 볼 수 있는데 이것을 Gimbal이라고 한다.
Gimbal은 한 축을 중심으로 회전할 수 있도록 매달린 링으로 일반적으로 여러 축을 중심으로 회전할 수 있도록 서로 중첩되어 있습니다.
각 링은 자신의 축으로만 회전을 한다. 다만, 바깥에 있는 링이 회전할 때 안쪽 링에도 영향을 끼친다
- 위에
SetActorRotation()에서 이 부분에 대해 설명을 했음
오일러 각
https://en.wikipedia.org/wiki/Euler_angles
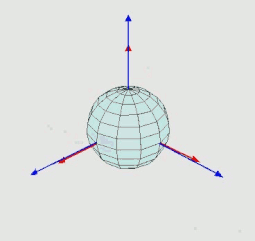
위의 위키피디아 링크를 들어가보면 그림과 같은 구 모형이 회전하는 걸 볼 수 있다.
오일러 각 : 3차원 공간에서 물체의 회전을 나타내는 방법 중 하나로, 3개의 회전각(X, Y, Z)을 사용하고 각 축에 대해 한 번씩만 회전하여(총 3번 회전) 좌표계를 변환하는 방식을 사용
- 일반적인 오일러 각 (XYZ, ZYX 등)
- 오일러 각을 사용할 때는 세 번의 회전 중 같은 축이 중복되지 않는 조합을 사용합니다.
- XYZ
- ZYX
- XZY
- YXZ
- YZX
- ZXY
- 두 축이 반복되는 경우 (XXY, YZZ 등)
- 만약 회전 순서가 XXY 또는 YZZ처럼 같은 축이 두 번 반복되면, 물체가 회전한 후 같은 축을 다시 기준으로 회전하는 게 의미가 없어지는 경우가 생길 수 있음
- 특정한 각도에서 회전 자유도가 사라지는 짐벌 락(Gimbal Lock) 현상이 더 쉽게 발생할 수 있음
오일러 각의 조합이 뜻하는 것은 회전 변환을 할 때, 해당 조합 순서로 회전을 한다는 의미이다
오일러 각 변환을 [ Z→Y→X ] 순으로 한다고 가정하면
- 처음 회전각 A를 Z축에 대해서 회전시키면 A'의 상태가 되고,
- 다음으로 Y축에 대해 회전할 때는 A에 대해서 Y축으로 회전하는 것이 아니라 A'에 대해서 Y축으로 회전하는 것이기 때문에 A"이 된다.
- 그리고 마지막으로 X축에 대해서 회전시킬 때는 A'이 아니라 A"에 대해서 회전시켜 A'''이 되는 것이다.
이미 Y축으로 돌릴 차례에는 Z축으로 돌아간 상태이기 때문에 두 축에 대한 계산이 독립적일 수가 없다. => 축으로 회전을 하고 나면 다음 축에 영향을 끼치는 게 Gimbal과 비슷함
번외로 최종 회전 행렬 R을 구하기 위해 각 축에 대한 회전 행렬 R_z(Z축), R_y(Y축), R_x(X축)가 있으면
- 최종 행렬 R = R_x * R_y * R_z 이다
- 변환 순서의 역순으로 곱함
- 행렬의 곱은 교환 법칙이 성립하지 않음 => 곱하는 순서가 중요
오일러 각에서도 gimbal lock이 발생한다는 데, 회전 행렬을 구해보면 그걸 알 수 있을 것 같은데
 |  |
|---|
두 값이 같음 => Gimbal Lock이 발생했다
Gimbal Lock
https://www.youtube.com/watch?v=zc8b2Jo7mno
Gimbal Lock : 회전 변환을 할 때 중간에 변환되는 축에 의해 첫번째 축과 세번째 축이 겹쳐져서 한 축에 대한 자유도가 사라지는 현상
참조 사이트
1. https://ko.wikipedia.org/wiki/%EC%A7%90%EB%B2%8C
2. https://en.wikipedia.org/wiki/Euler_angles
3. https://velog.io/@singery00/UE5-%EC%A7%90%EB%B2%8C-%EB%9D%BD-Gimbal-Lock
4. https://rhksgml78.tistory.com/263
5. https://handhp1.tistory.com/3
6. https://kangworld.tistory.com/185
7. https://www.youtube.com/watch?v=zc8b2Jo7mno
