영상 속의 물체 추적하기

칼만필터를 이용한 세번째 예제는 '영상 속의 물체를 추적하기'이다. 영상 처리 기법으로 찾아낸 물체의 위치를 입력 받아 정확한 위치를 추정하는 것이다.

시스템 모델 설정

$x=\begin{bmatrix}position_x \\ velocity_x \\ position_y \\ velocity_y \end{bmatrix}$ 1.1
$x_{k+1}=Ax_k+w_k$ 1.2
$z_k=Hx_k+v_k$ 1.3

가장 먼저 상태 변수(state variable)를 1.1과 같이 정의한다. 즉, 관심있는 물리량을 객체의 영상 내 위치로 설정한다. 이에 따라 행렬 $A$와 $H$는 다음과 같다.

$A=\begin{bmatrix}1 &\Delta t & 0 & 0\\0 & 1 & 0 & 0\\0 & 0 & 1 & \Delta t \\ 0 & 0 & 0 & 1\end{bmatrix}$

$H=\begin{bmatrix}1 & 0 & 0 & 0\\ 0 & 0 & 1& 0\end{bmatrix}$

$x_{k+1}=\begin{bmatrix}position \\ velocity \end{bmatrix}_{k+1}=\begin{bmatrix}1 & \Delta t \\0 & 1\end{bmatrix}\begin{bmatrix}position \\ velocity\end{bmatrix}_k+\begin{bmatrix}0 \\ w_k\end{bmatrix}$ 2.1

$A$의 경우 2.1에서 볼 수 있듯이 '현재 위치= 직전 위치 + 이동 거리' 라는 기본적인 물리 법칙이다. $H$의 경우 $x$축과 $y$축 방향의 위치만 측정하고 속도는 측정하지 않는다는 의미이다. 마지막으로 잡음의 공분산 행렬인 $(Q,R)$을 결정해야 한다. 이 예제에서는 두 잡음을 다음과 같이 설정한다.

$Q=\begin{bmatrix}1 & 0 \\ 0 & 1\end{bmatrix}$

$R=\begin{bmatrix}50 & 0 \\ 0 & 50\end{bmatrix}$

알고리즘

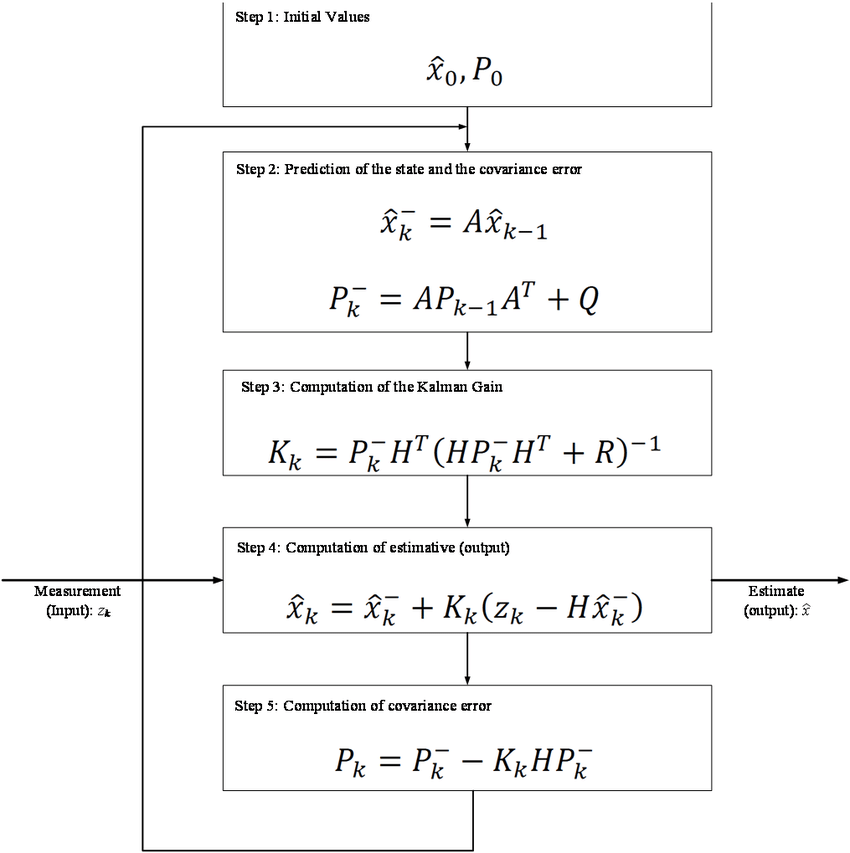
코드

function [xh, yh] = TrackKalman(xm, ym)

persistent A H Q R
persistent x_hat P
persistent firstRun

if isempty(firstRun)
    dt = 1; % 1 Hz

    A = [1, dt, 0, 0
         0, 1, 0, 0
         0, 0, 1, dt
         0, 0, 0, 1];

    H = [1, 0, 0, 0
         0, 0, 1, 0];

    Q = 1.0 * eye(4);
    R = 50.0 * eye(2);
    
    %{
    x_hat = [pos_x
             vel_x
             pos_y
             vel_y]
    %}
    x_hat = [0, 0, 0, 0]'; 
    P = 100 * eye(4);

    firstRun = 1;
end

xp = A*x_hat;
Pp = A*P*A' + Q;
K = Pp*H' * inv(H*Pp*H' + R);

z = [xm, ym]';
x_hat = xp + K*(z - H*xp);
P = Pp - K*H*Pp;

% 추정 위치 반환
xh = x_hat(1);
yh = x_hat(3);

결과

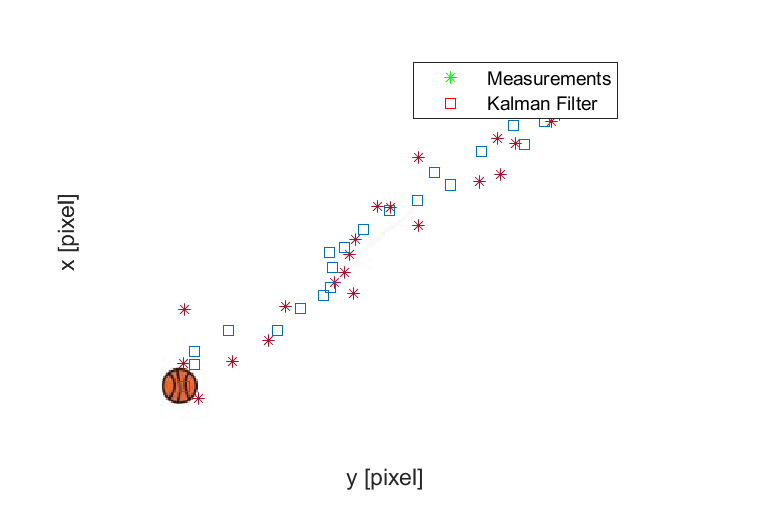
결과 화면에서는 확인할 수 없지만 코드를 처음 실행 시 Kalman Filter에 의한 추정값은 전혀 엉뚱한 곳을 가리키고 있었다. 이에 따라 실험적으로 행렬 Q와 R을 수정해가며 칼만 필터의 성능을 개선해야된다는 사실을 알 수 있었다.

참고

칼만 필터는 어렵지 않아 - 김성필 저, 한빛아카데미