위치로 속도 추정하기

칼만필터를 이용한 두번째 예제는 '직선 선로에서 열차의 속도가 80m/s를 유지하는지 위치 정보만을 토대로 추정하기이다. 즉, 위치 정보만으로 측정하지도 않은 속도를 추정하는 것이다.

시스템 모델 설정

$x=\begin{bmatrix}position \\ velocity \end{bmatrix}$ 1.1
$x_{k+1}=Ax_k+w_k$ 1.2
$z_k=Hx_k+v_k$ 1.3

가장 먼저 상태 변수(state variable)를 1.1과 같이 정의한다. 즉, 관심있는 물리량을 열차의 위치와 속도로 설정한다. 이에 따라 행렬 $A$와 $H$는 다음과 같다.

$A=\begin{bmatrix}1 &\Delta t\\0 & 1\end{bmatrix}$
$H=\begin{bmatrix}1 & 0\end{bmatrix}$

$x_{k+1}=\begin{bmatrix}position \\ velocity \end{bmatrix}_{k+1}=\begin{bmatrix}1 & \Delta t \\0 & 1\end{bmatrix}\begin{bmatrix}position \\ velocity\end{bmatrix}_k+\begin{bmatrix}0 \\ w_k\end{bmatrix}$ 2.1
$z_k=\begin{bmatrix}1 &0\end{bmatrix}\begin{bmatrix}position \\ velocity\end{bmatrix}_k+v_k$ 2.2

$A$의 경우 2.1에서 볼 수 있듯이 '현재 위치= 직전 위치 + 이동 거리' 라는 기본적인 물리 법칙이기 때문이다. $H$의 경우도 마찬가지로 2.2에서 확인 가능하며 예제의 전제 조건이 측정값이 위치 정보만 존재하기 때문이다.
만약 전제 조건이 반대로 측정값에는 속도 정보만 존재하고 위치를 추정해야 한다면 $H=\begin{bmatrix}0 & 1\end{bmatrix}$과 같이 설정될 것이다.
마지막으로 잡음의 공분산 행렬인 $(Q,R)$을 결정해야 한다. 측정 잡음($v_k$)의 경우 대부분 센서 제조사의 데이터 시트로 제공되는 경우가 있기 때문에 이를 확인하여 $R$을 결정할 수 있다. 시스템 잡음($w_k$)의 모델링은 시스템에 대한 경험에 의존하여 결정할 수 밖에 없다. 이 예제에서는 두 잡음을 다음과 같이 설정한다.

$Q=\begin{bmatrix}1 & 0 \\ 0 & 3\end{bmatrix}$
$R=10$

알고리즘

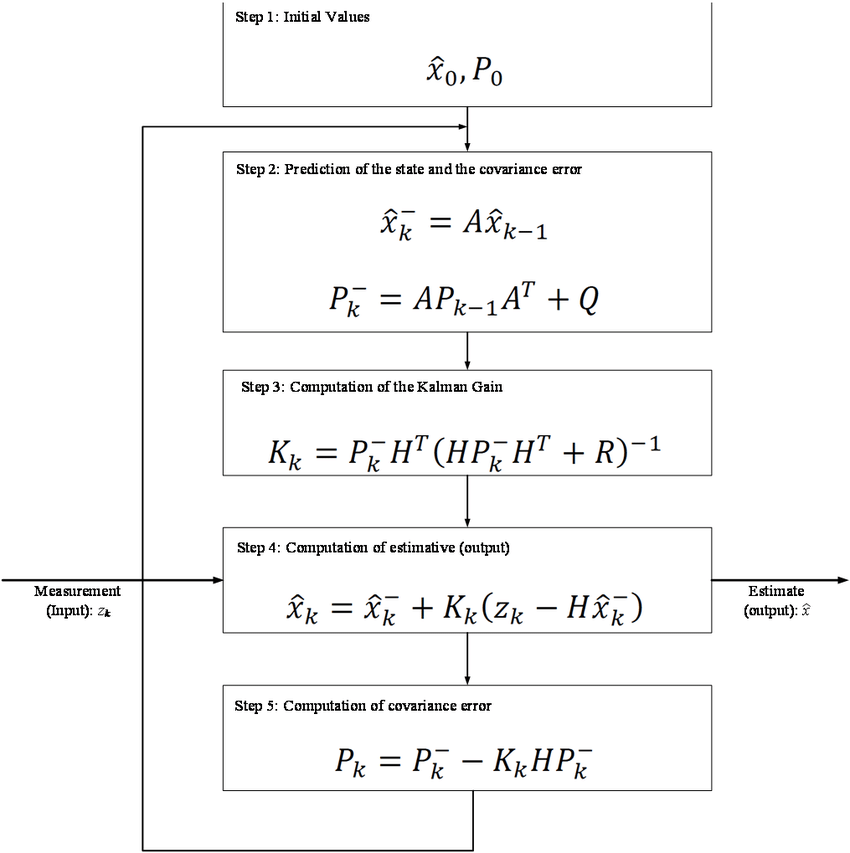
코드

function [pos, vel] = DvKalman(z)

persistent A H Q R
persistent x_hat P
persistent firstRun

if isempty(firstRun)
    firstRun = 1;

    dt = 0.1; % Sampling Time

    A = [1, dt;
         0, 1]; % Position_(k+1) = Position_k + (Velocity_k * dt)

    H = [1, 0]; % Z_k = Position_k + v_k

    Q = [1, 0;
         0, 3];
    
    R = 10; % Usually provided by sensor manufacturer

    x_hat = [0, 20]'; % x_0(Initial state)
    P = 5 * eye(2); % P_0(Initial state)
end

xp = A * x_hat;
Pp = A*P*A' + Q;

K = Pp*H'*inv(H*Pp*H' + R);

x_hat = xp + K*(z - H*xp);
P = Pp - (K*H*Pp);

pos = x_hat(1);
vel = x_hat(2);

결과

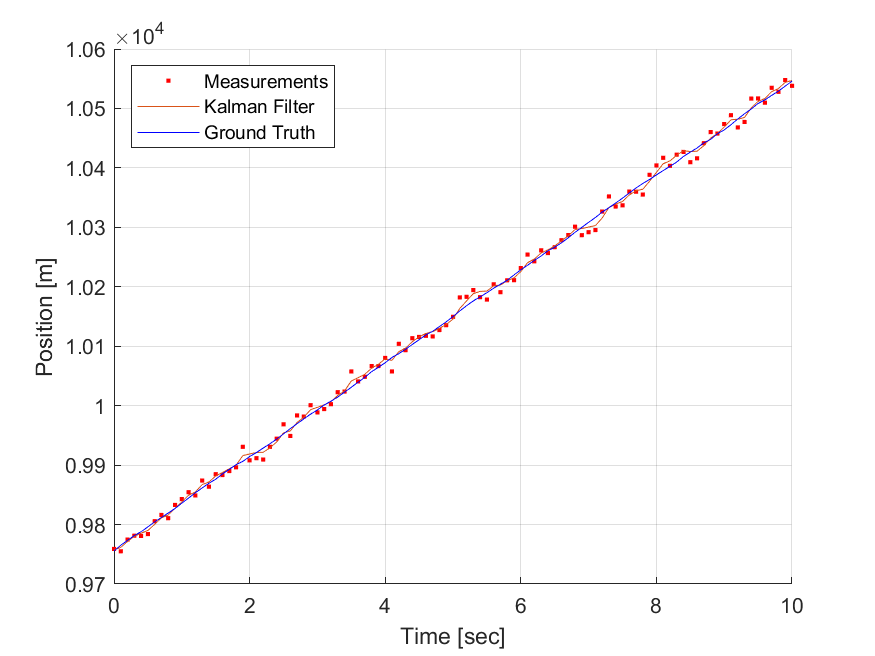
각 plot마다 Ego vehicle의 ground truth값과 measurement 그리고 Kalman filter를 통하여 필터링된 결과를 시각화하였다. 결론적으로 칼만 필터가 측정하지 않은 물리량까지 추정해내는 능력은 '시스템 모델'을 이용하였기 때문이다. 상태 변수 사이의 연관 관계를 나타내는 시스템 모델을 통해 즉정하지 않는 상태 변수를 간접적으로 추정하기 때문이다. 따라서 시스템 모델이 실제 시스템과 상이할 경우 칼만 필터가 발산하여 전체 시스템의 성능이 떨어진다.

참고

칼만 필터는 어렵지 않아 - 김성필 저, 한빛아카데미