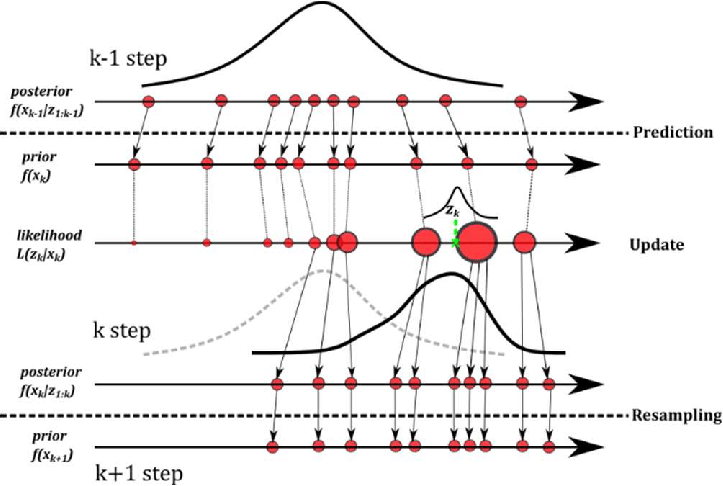
파티클 필터

파티클 필터는 칼만 필터와 달리 상태 변수가 가우시안 분포를 따르지 않는 시스템에도 적용이 가능한 비선형 필터이다. 파티클 필터는 '파티클'이라고 불리는 것을 통해 비선형 모델의 확률 분포를 모사한다. 즉, 파티클만으로 시스템의 확률 분포와 상태 등을 모두 표현한다. UKF와 비슷한 점은 모든 파티클의 가중합이 상태 변수의 추정값이 된다.

Unscented Kalman Filter

• $x\sim N(x_m=\hat{x}_k, P_x)$

• $x_m=\Sigma_{i=1}^{2n+1}W_i\chi_i$

Particle Filter

• $\hat{x}_k=\Sigma_{m=1}^{N}p_m^-w_m$

알고리즘

가장 먼저 EKF와 UKF와 동일하게 비선형 시스템 모델을 정의하면 다음과 같다.

$x_{k+1}=f(x_k)+w_k$
$z_k=h(x_k)+v_k$

여기서 가장 중요한 점은 칼만 필터와 달리 파티클 필터는 $w_k,v_k$가 가우시안 분포 뿐만 아니라 임의의 확률 분포를 따를 수 있다는 점이다.

---

0단계: 파티클 초기화

• $[p_m, w_m],\quad\quad m=1,2,\dots,N$

지정된 갯수($N$)의 파티클($p_m$)과 가중치($w_m$)를 초기화 한다. 예측과 추정과정을 모두 이 파티클들과 각 파티클의 해당 가중치를 기반으로 진행한다.

---

1단계: 파티클 예측

• $p_m^-=f(p_m)$

시스템 모델을 통해 각 파티클의 예측값을 구한다.

---

2단계: 파티클 가중치 갱신

• $w_m=w_m\,p(z_k|z_m^-)$
• $w_m=\frac{w_m}{\Sigma w_m}$

파티클의 가중치를 갱신한다. 이때 가중치를 갱신하는 방법은 측정값($z_k$)과 각 파티클 예측 측정값($z_m^-)$의 차이를 기반으로 갱신된다. 측정값과 예측 측정값이 비슷할수록 해당 파티클의 가중치가 커진다. 그 후에 가중치를 0~1사이의 값으로 정규화하는 과정을 거치게 된다.

---

3단계: 추정값 계산

• $\hat{x}_k=\Sigma_{m=1}^Np_m^-w_m$

각 파티클의 가중치를 고려한 가중합으로 추정값을 계산한다.

---

4단계: 재샘플링

• $p_m=resample(p_m^-),\quad\quad m=1,\dots,N$
• $w_m=\frac{1}{N}$

리샘플링이라는 과정을 통해 각 파티클의 가중치를 반영해 파티클을 새로 생성한다. 리샘플링을 하는 방법으로는 다양한 알고리즘이 존재하는데 이 책에서는 순차적 중요도 재샘플링 SIR(Sequence Importance Resampling)만을 다룬다. 새로 생성된 파티클들의 가중치는 동일하게 $\frac{1}{N}$로 초기화한다. 마무리 되면 1단계로 다시 되돌아가 일련의 과정을 실행한다.

---

레이더 추적 예제

예제는 이전과 동일하게 '레이더로 물체까지의 거리를 측정해서 이동 속도와 고도를 추정하기'이다. 이 예제에서 물체는 2차원 평면 상에서 일정한 고도와 속도를 유지하면서 움직인다고 가정한다.

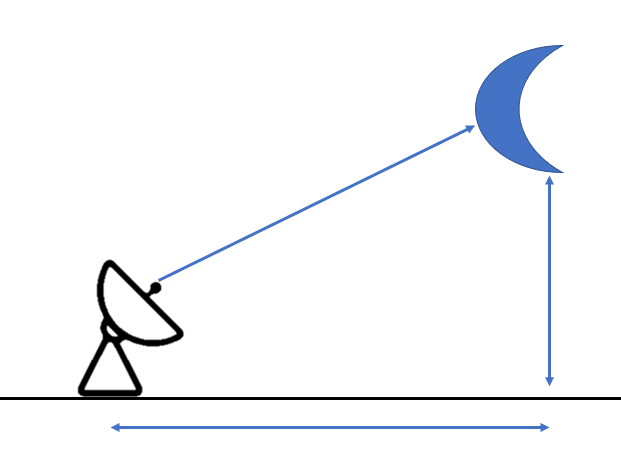
시스템의 상태 변수를 다음과 같이 설정한다.

$x=\begin{bmatrix}수평거리\\이동 속도\\고도\end{bmatrix}=\begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix}$ 3.1

전제조건에서 물체의 이동 속도와 고도가 일정하다고 주어졌으므로 시스템 모델은 다음과 같이 표현된다.

$\begin{bmatrix}\dot{x_1}\\\dot{x_2}\\\dot{x_3}\end{bmatrix}=\begin{bmatrix}0&1&0\\0&0&0\\0&0&0\end{bmatrix} \begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix}+\begin{bmatrix}0\\w_1\\w_2\end{bmatrix}$ 3.2

수평 거리의 변화율이 물체의 이동속도이므로 3.3임을 알 수 있다. 또한 이동 속도와 고도가 일정하므로 변화율이 0이다. 하지만 시스템 잡음을 고려하여 $w_1, w_2$를 추가한다.

$\dot{x_1}=x_2$ 3.3
$\dot{x_2}=w_1$ 3.4
$\dot{x_3}=w_2$ 3.5

또한, 레이더의 측정값($z_k$)은 측정 잡음($v$)를 고려하여 4.1과 같이 표현된다.

$z_k=r=\sqrt{x_1^2+x_3^2}+v=h(x)+v$ 4.1

코드

function [pos, vel, alt] = RadarPF(z, dt)

persistent x  % 상태변수=[수평거리, 이동속도, 고도]'
persistent firstRun
persistent pt wt  % 파티클들의 위치와 가중치
persistent Npt  % 파티클의 갯수


if isempty(firstRun)
    x = [0, 90, 1100]';

    Npt = 1000;

    pt(1, :) = x(1) + 0.1*x(1) * randn(1, Npt);
    pt(2, :) = x(2) + 0.1*x(2) * randn(1, Npt);
    pt(3, :) = x(3) + 0.1*x(3) * randn(1, Npt);

    wt = ones(1, Npt) / Npt;

    firstRun = 1;
end

% I) 파티클 예측: 시스템 모델을 통해 각 파티클의 예측값을 구함
for k=1:Npt
    pt(:, k) = fx(pt(:, k), dt) + randn(3, 1);
end

% II) 파티클 가중치 갱신: 측정값과 각 파티클 예측 측정값의 차이를 기반으로 파티클의 가중치를 갱신
for k=1:Npt
    wt(k) = wt(k) * normpdf(z, hx(pt(:, k)), 10); % 가중치 변경
end
wt = wt / sum(wt);  % 가중치 정규화

% III) 추정값 계산: 각 파티클의 가중치를 고려한 가중합으로 추정값 계산
x = pt * wt';
pos = x(1);
vel = x(2);
alt = x(3);

% IV) 재샘플링 과정(Sequence Importance Resampling): 각 파티클의 가중치에 비례해 해당 파티클의 갯수를 조절
[pt, wt] = resampling(pt, wt, Npt);

%--------------------------
function xp = fx(x, dt)

A = eye(3) + dt * [0, 1, 0;
                   0, 0, 0;
                   0, 0, 0];
xp = A*x;
%--------------------------
function zp = hx(xhat)
x1 = xhat(1);
x3 = xhat(3);

zp = sqrt(x1^2 + x3^2);

• 1) Npt는 파티클의 갯수를 나타낸다. 파티클들의 위치와 가중치는 각 pt, wt에 저장된다. 각 파티클의 초기 위치는 상태 변수 초기값을 중심으로 정규 분포에 따라 배치하고, 가중치는 모두 $\frac{1}{Npt}$로 초기화한다. 예측 과정에서 파티클(pt)를 시스템 모델(fx)에 통과시켜 새로운 위치를 얻는다.

• 2) 예측 과정이 완료되면 실제 측정값인 z와 각 파티클의 예측 측정값($p_m^-$)을 나타내는 hx(pt(:, k))를 비교하여 해당 파티클의 가중치를 바꿔준다. 즉 실제 측정값과 가장 근접한 예측 측정값을 갖는 파티클의 가중치를 높여주는 역할을 하게 된다.

• 3) 이렇게 모든 파티클들의 가중치가 조절되면, 다시 가중치의 총합이 1이 되도록 정규화한다.

• 4) 이 과정을 반복하게 되면 일부 파티클의 가중치만 커지고, 나머지 파티클은 제 역할을 하지 못하게 된다. 따라서 파티클을 다음 스텝의 예측 과정에서 사용하기 전에 재샘플링(SIR) 과정을 거친다.

Resampling

function [pm, wm] = resampling(pt, wt, Npt)

% 1단계: % 각 구간에 해당 파티클의 가중치에 비례한 길이를 할당
wtc = cumsum(wt);

% 2단계: Uniform Distribution를 따르는 0~1 사이의 값을 Npt 개수만큼 새로 생성
rpt = rand(Npt, 1);

% 3단계: 1단계에서 할당한 구간마다 2단계에서 생성한 값이 몇개 들어있는지를 카운트
[~, ind1] = sort([rpt; wtc']);
ind = find(ind1 <= Npt) - [0:Npt-1]';

% 4단계: 각 구간에 포함된 값의 개수만큼 해당 파티클의 개수 조절(리샘플링), 2단계에서 생성한 값이 하나도 들어있지 않다면 해당
% 파티클은 버린다. 즉 이 파티클은 다음 예측 과정에 사용되지 않는다. 여러 개의 값이 포함되어 있다면 해당 파티클은 그 개수만큼
% 중복해서 생성한다.
pm = pt(:, ind);

% 5단계: 새로 재샘플링된 파티클의 가중치를 모두 동일하게 (1/Npt)로 설정
wm = ones(1, Npt) / Npt;

결과

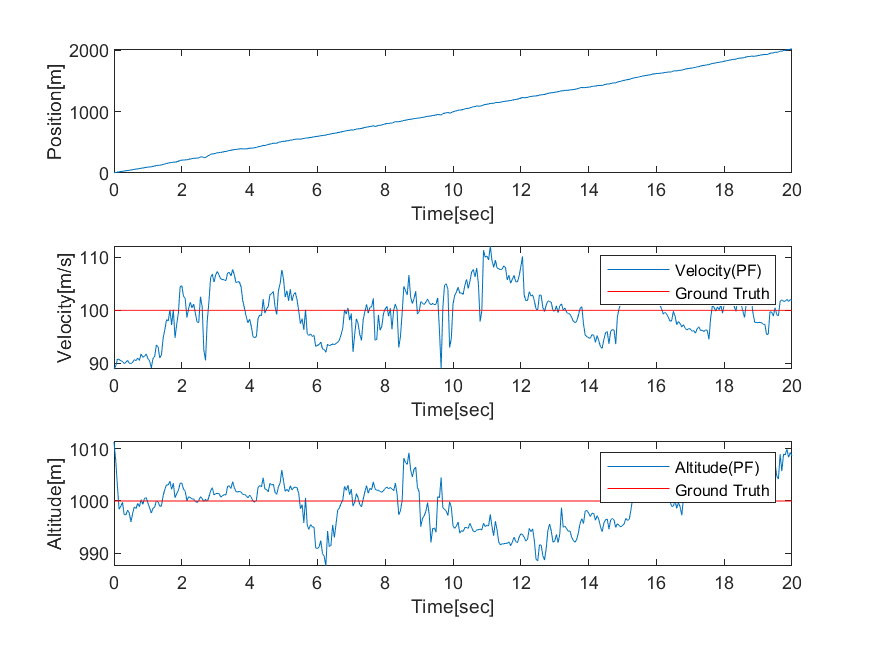
참고

칼만 필터는 어렵지 않아 - 김성필 저, 한빛아카데미