Complimentary Filter

soup1997·2023년 2월 22일

Sensor fusion complimentary filter filter

칼만필터는 어렵지 않아

목록 보기

13/14

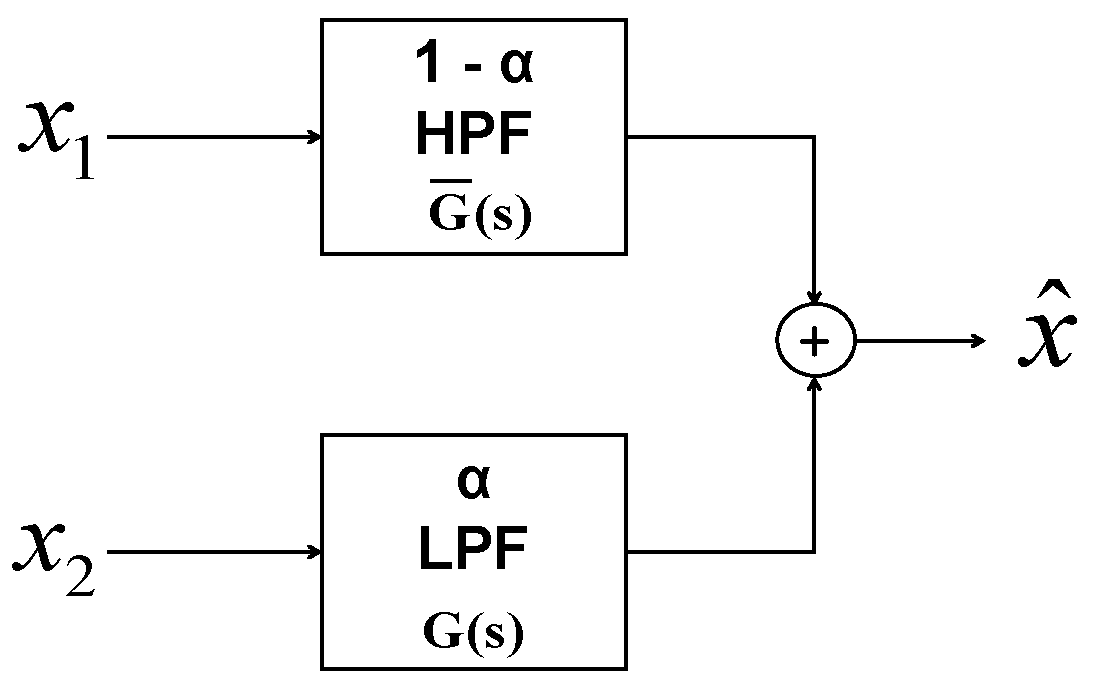
상보 필터

Complimentary filter는 Kalman filter과 동일하게 여러 개의 센서를 융합하여 더 나은 측정값을 얻고자 할 때 사용한다. 주목할 특징은 센서의 주파수 특성이 보완적일 때만 사용이 가능하다는 점이다. 이는 두 센서의 저주파 성분과 고주파 성분을 적절히 융합해 개별 센서의 측정값보다 더 우수한 측정값을 얻어내게 된다는 말이다. 썸네일의 그림에서 확인할 수 있듯이 각 측정잡음의 특성에 맞춰 필터 $G(s)$ 와 $\overline{G(s)}$ 를 통과하여 합산한 값이 최종 결과 값이 된다. 상보 필터는 다음과 같은 구조가 되도록 시스템을 구성한다.

$G(s)=\alpha$
$\overline{G(s)}=1-\alpha$

최종 출력값인 $\hat{x}$ 는 2.2와 같은 수식을 전개함으로써 구할 수 있다. 가장 먼저 입력 신호인 $x_1$ 과 $x_2$ 는 잡음을 고려하여 나타내면 1.1, 1.2와 같다. 또한, 각각의 센서가 동일한 물리량을 측정한다면 $x_1(t)=x_2(t)$ 로 가정할 수 있다. 이에 따라 주파수 관점에서 상보 필터를 분석해야 하므로 라플라스 변환이 필요하다.

$x_1=x_1(t)+n_1(t)$ 1.1
$x_2=x_2(t)+n_2(t)$ 1.2

$X(s)=X_1(s)=X_2(s)$ 2.1
$\hat{X(s)}=(1-G(s))(X_1(s)+N_1(s))+G(s)(X_2(s)+N_2(s))$
$\quad\quad\;\,=X(s)+(1-G(s))N_1(s)+G(s)N_2(s)$ 2.2

참값인 $X(s)$ 는 필터 $G(s)$ 의 영향을 전혀 받지 않는다는 것에 대해 주목해야 한다. 측정 물리량의 참값은 어떠한 형태로도 변형되지 않는다는 것이다. 이에 따라 전달함수의 영향을 받는 신호는 각 센서의 측정 잡음인 $N_1(s)$ 와 $N_2(s)$ 가 된다.

세 개의 Measurement source로 확장

만약 측정 센서가 세 개 이상일 경우라면 상보 필터를 구성하는 필터의 합이 1이 되도록 구성하면 된다.

$G_1(s)$ = 측정값 1에 대한 필터의 전달 함수
$G_2(s)$ = 측정값 2에 대한 필터의 전달 함수
$G_3(s)=1-G_1(s)-G_2(s)$ = 측정값 3에 대한 필터의 전달 함수

자이로-가속도계 융합 상보 필터

상보 필터를 사용하기 위해 각 센서의 특성을 분석해보면 다음과 같다. 결국 두 센서의 오차특성은 오일러 각도를 계산하기 위한 적분 과정의 유무가 근본적인 원인이 되기 때문에 이것이 두 센서의 주파수 특성을 반영하게 된다.

자이로: 장시간 사용할수록 누적오차로 인해 오차 증가, 단기적인 변화에 효과적
가속도계: 장시간 사용해도 누적오차 X, 가속도에 잡음이 유입되는 순간만 오차 발생

PI제어기를 이용하여 정리한 최종적인 상보 필터의 수식은 다음과 같다.

$\phi_m=[1-G(s)](\frac{1}{s}\dot\phi_g)+G(s)\phi_a$
$G(s)=\frac{sK_p+K_i}{s^2+sK_p+K_i}$

$\phi_m$ : 최종 Roll 값
$\dot{\phi_g}$ : 자이로 Roll rate 값
$\phi_a$ : 가속도 Roll 값
$G(s)$ : Lowpass Filter

코드

function [phi, theta, psi] = CompFilterWithPI(p, q, r, ax, ay, az, dt)

persistent p_hat q_hat
persistent prevPhi prevTheta prevPsi

if isempty(p_hat)
    p_hat = 0;
    q_hat = 0;

    prevPhi = 0;
    prevTheta = 0;
    prevPsi = 0;
end

[phi_a, theta_a] = EulerAccel(ax, ay, az);

[dotPhi, dotTheta, dotPsi] = BodyToInertial(p, q, r, prevPhi, prevTheta);

phi = prevPhi + dt * (dotPhi - p_hat);
theta = prevTheta + dt * (dotTheta - q_hat);
psi = prevPsi + dt * dotPsi;


p_hat = PILawPhi(phi - phi_a);
q_hat = PILawTheta(theta - theta_a);

prevPhi = phi;
prevTheta = theta;
prevPsi = psi;

function [dotPhi, dotTheta, dotPsi] = BodyToInertial(p, q, r, phi, theta)

sinPhi = sin(phi);
cosPhi = cos(phi);
cosTheta = cos(theta);
tanTheta = tan(theta);

dotPhi = p + q*sinPhi*tanTheta + r*cosPhi*tanTheta;
dotTheta = q * cosPhi - r*sinPhi;
dotPsi = q*sinPhi/cosTheta + r*cosPhi/cosTheta;

function p_hat = PILawPhi(delPhi)

persistent prevP prevdelPhi

if isempty(prevP)
    prevP = 0;
    prevdelPhi = 0;
end

p_hat = prevP + 0.1415*delPhi - 0.1414*prevdelPhi;

prevP = p_hat;
prevdelPhi = delPhi;

function q_hat = PILawTheta(delTheta)

persistent prevQ prevdelTheta

if isempty(prevQ)
    prevQ = 0;
    prevdelTheta = 0;
end

q_hat = prevQ + 0.1415*delTheta - 0.1414*prevdelTheta;

prevQ = q_hat;
prevdelTheta = delTheta;

이 코드에서 비례-적분 제어기는 3과 같은 전달함수의 형태를 띄고 있다. 라플라스는 연속적인 신호를 주파수 영역에서 분석하므로 이를 이산 신호로 분석하기 위해선 z변환이 필요하다.