평균 필터

평균필터는 데이터가 $k$개임을 미리 알고 있을때 사용할 수 있는 필터이다. 일반적으로 $k$개의 평균을 구하는 방법은 가장 쉽게 다음과 같은 수식으로 이루어진다.

$\overline{x_k} = \frac{x_1 + x_2 + \dots + x_k}{k}$

하지만, 이러한 수식은 앞서 계산한 스텝($k-1$번째)의 평균은 전혀 이용하지 않으며 매 스텝마다 평균을 새로 계산한다는 연산의 부하에 대한 단점이 존재한다. 이를 해결하기 위해 이전 스텝의 평균값을 이용할 수 있도록 재귀식(recursive expression) 형태로 위의 식을 변경하여 최종적으로 다음과 같은 형태를 유도할 수 있게 된다. (증명과정은 생략)

$\overline{x_{k}} = \frac{k-1}{k}\overline{x_{k-1}}+\frac{1}{k}x_k$

여기서 $\alpha = \frac{k-1}{k}$ 라고 정의하며 치환하면 위의식은 다음과 같은 형태로 바뀌게 된다.

$\overline{x_{k}} = \alpha\overline{x_{k-1}}+(1-\alpha)x_k$

예를 들어, 어떤 데이터의 7개의 평균을 구한다 가정하면 $\alpha=0.85, 1-\alpha=0.15$값이 되며 즉 $\alpha$는 $0 < a <1$의 범위를 가지게 되는 것을 알 수 있다. 결론적으로, IMU와 같이 어떠한 시점의 특정 값을 기준으로 상대적인 각도와 가속도를 측정하는 센서에서도 이를 초기화 할때 유용하게 쓰인다. 즉 영점을 잡는 초기화 작업이 필요한 센서에 모두 응용될 수 있다.

평균필터 예제

plot1

%{
persistent는 C언어의 Static(정적 변수)와 같은 역할
%}

function avg = AvgFilter(x)

persistent prevAvg k
persistent firstRun % Flag 변수

if isempty(firstRun) % 함수 초기화
    k = 1;
    prevAvg = 0;

    firstRun = 1;
end

alpha = (k-1)/ k;
avg = alpha * prevAvg + (1-alpha) * x;

prevAvg = avg;
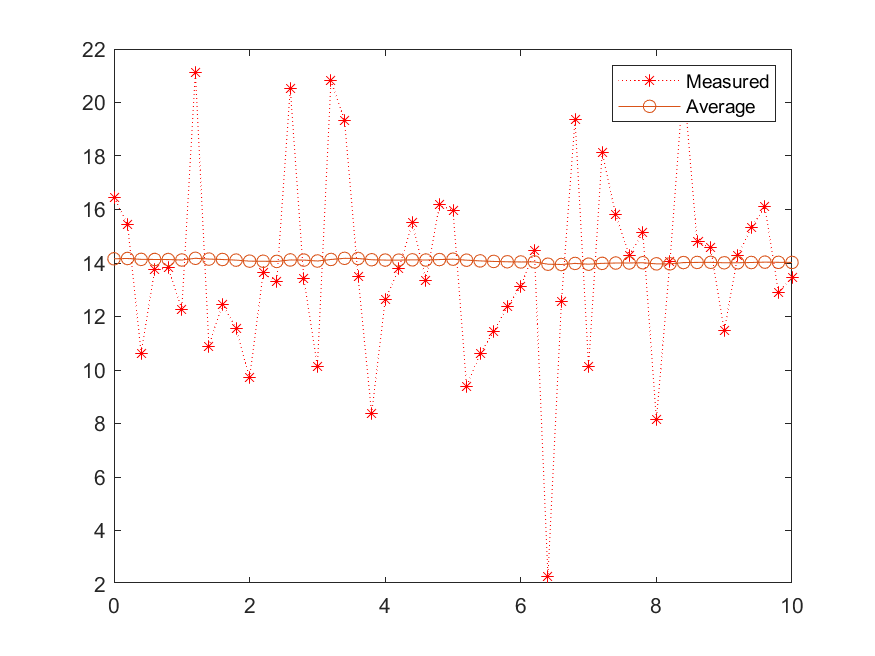
k = k + 1; % 매 스텝마다 k값 1씩 증가

plot1의 경우 새로운 신호가 입력될때마다 $k$값(평균 갯수)을 1씩 증가 시켜 최종적으로 반복문이 종료되면 전체 데이터 갯수에 대한 필터링된 신호가 구해지게 된다. 원 신호의 노이즈가 굉장히 많은 것에도 불구하고 평균필터를 통해 Target Value인 14.4에 가깝게 출력되는 것을 확인할 수 있었다. 이처럼 특정 값에 일정한 출력이 필요할 경우 데이터가 입력될때마다 $k$값을 증가시키는 방식으로 일정한 출력을 얻을 수 있게 된다.

plot2

%{
persistent는 C언어의 Static(정적 변수)와 같은 역할
%}

function avg = AvgFilter(x)

persistent prevAvg k
persistent firstRun % Flag 변수

if isempty(firstRun) % 함수 초기화
    k = 1;
    prevAvg = 0;

    firstRun = 1;
end

alpha = (k-1)/ k;
avg = alpha * prevAvg + (1-alpha) * x;

prevAvg = avg;
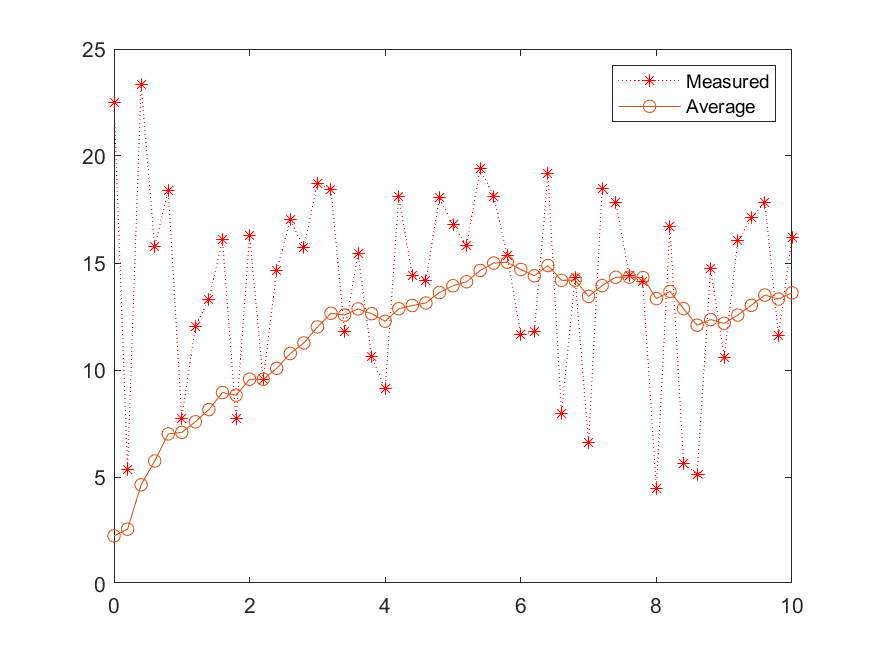
k = 10; % 매 스텝마다 k값 1씩 증가

반면 plot2는 조금 다른 경우인데 $k$값을 데이터가 입력될 때마다 증가시키지 않고 $k=10$으로 고정하였다. plot1 비해서 14.4라는 값이 일정하게 유지되진 않지만 원 신호를 어느정도 따라가는 경향을 띄고 있다. 평균필터는 데이터의 갯수인 $k$개의 평균을 구하는 필터이다. 따라서 위의 plot은 평균필터가 아닌 일종의 저주파 통과필터의 노이즈 제거효과이다. 저주파 통과필터는 추후 포스트에서 다루겠다.

참고

칼만 필터는 어렵지 않아 - 김성필 저, 한빛아카데미