이동 평균 필터

이동평균필터는 개인적으로 가장 처음으로 접해본 필터 중 하나라고 말할 수 있다. 학부생 시절 자율주행 경진대회에 참가했을 때 차선인식을 통해 소실점을 기준으로 차량의 조향각을 계산하였다. (적절한 방법은 곡률 기반으로 하는게 맞다.)
어쨌든, 차량의 조향각을 안정화 시키기 위해 이동평균 필터를 이용했지만 당시에는 원리나 수식은 전혀 이해못했다. 서론이 길었으니 바로 본론으로 가겠다.

n개의 데이터에 대한 이동평균
$\overline{x_k}=\frac{x_{k-n+1}+x_{k-n+2}+\dots+x_k}{n}$

이동평균의 $\overline{x_k}$는 $k-n+1$번째 데이터부터 $k$번째 데이터까지 총 $n$개 데이터의 평균을 의미한다. 즉, 분자항의 데이터의 갯수가 항상 $n$으로 고정되어 있다.
평균필터와 마찬가지로 재귀식으로 변경하기 위해 이전스텝의 이동평균은 다음과 같다.

이전 스텝의 이동평균
$\overline{x_{k-1}}=\frac{x_{k-n}+x_{k-n+1}+\dots+x_{k-1}}{n}$

두식을 빼면 최종적으로 다음과 같이 정리된다.

이동평균 필터
$\overline{x_k} - \overline{x_{k-1}}= \frac{x_k - x_{k-n}}{n}$
$\overline{x_k}=\overline{x_{k-1}} + \frac{x_k - x_{k-n}}{n}$

가장 두드러지는 특징은 총합을 구하는 데이터 갯수는 $n$개로 항상 일정하다는 것이다. 또한, 직전 이동평균($\overline{x_{k-1}}$)과 가장 오래된 데이터($x_{k-n}$)가 필요하다.

이동평균 필터 예제

function avg = MovAvgFilter(x)

persistent n xbuf
persistent firstRun

if isempty(firstRun)
    n = 10; % 10개의 데이터에 대한 평균을 구함
    xbuf = x * ones(n, 1); % 이동평균 필터 적용을 위한 buffer 생성
    firstRun = 1;
end


% Queue의 FIFO 특성을 이용하여 구현하는게 더 간편함
for m=1:n-1
    xbuf(m) = xbuf(m+1); % 데이터 앞으로 옮기기
end

xbuf(n) = x; % 현재 스텝에 입력된 데이터


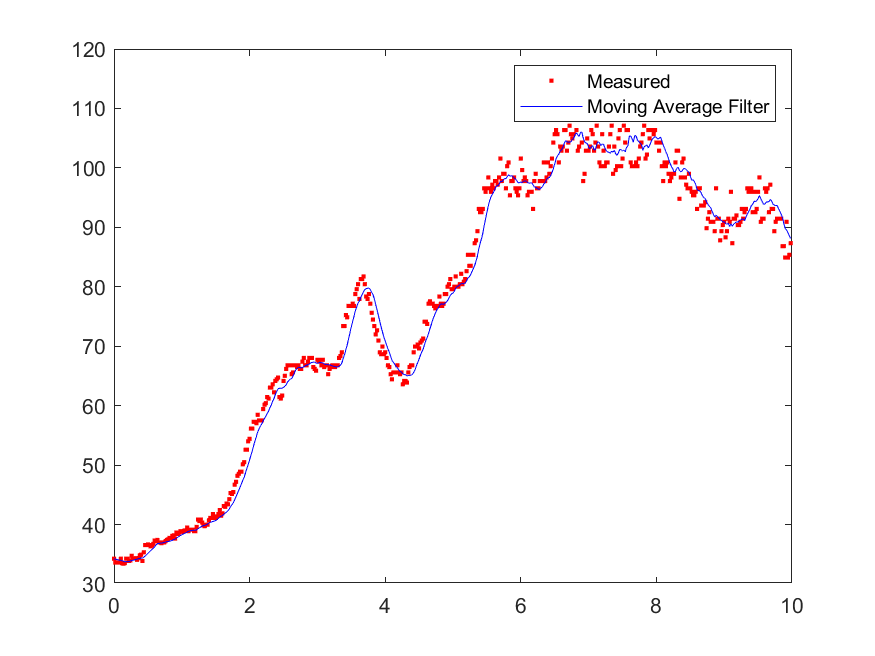
avg = sum(xbuf) / n;

이동평균 필터는 측정 데이터의 잡음을 제거하는데 유용하다. 평균 계산에 포함되는 데이터 개수가 많으면 잡음 제거 성능은 좋아지지만 측정 신호의 변화가 제때 반영되지 않고 시간지연이 발생한다. 반대로 데이터 개수가 적으면 측정 신호의 변화는 잘 따라가지만 잡음이 잘 제거되지 않는다. 결론적으로 파라미터인 $n$을 어떻게 설정하느냐에 따라서 시스템의 성능이 결정된다고 볼 수 있겠다.

참고

칼만 필터는 어렵지 않아 - 김성필 저, 한빛아카데미