AVL Tree

여기에 정리할 요약 노트의 원 강의는 MIT 6.006 Introduction to Algorithms, Spring 2020이다.

Binary Search Tree (Set Binary Tree)

Finding a certain item can be done with binary search if the nodes are ordered so that the keys the nodes represent are in an increasing order

• subtree_find(node, k): if node is not to be found, return. If k < node.item.key, recurse on node.left. If equal, return the node as this is the node we intended to look for. If k > node.item.key, recurse on node.right. As you can see, it is the same as binary search
  

Sequence Binary Tree

Its traversal order is the sequence order. The challenge is to find the ith node in the subtree. Knowing the size of the subtree is crucial and the size of a node means the number of nodes in the subtree, including the node itself

• subtree_at(node, i): Set an arbitrary variable NL to the size of node.left(the subtree on the left in the picture above). Suppose we know the value of the size somehow. So the index* of the root node is NL. If i < NL then recurse on node.left. If i = NL, return the current node. Lastly, if i > NL then do subtree_at(node.right, i-NL-1) recursively. We readjust the NL’s value to i-NL-1 because we don’t need node.left(NL) and the root node(1) so we subtract them. This operations takes O(height) * when dealing with set binary trees, keys were used; here, indices are used with sequence objects
  

Subtree Augmentation

Each node can store O(1) extra fields/properties. Subtree property can be computed from properties of its left or right children in O(1) time. Size of a sequence binary tree is a property as node.size = node.left.size + node.right.size + 1(itself). If every node has its size as its property, we can get a size of a particular node in constant time. Common properties include sum, min, max of some feature of every node in subtree.

However, you cannot store the index or depth of each node as once a new node is added, every node’s index changes and a node’s index doesn’t necessarily depend on the subtree it belongs to. For example, the index of the first node in node.right right below the root is solely reliant on the number of nodes in node.left and root.

When a new leaf is added or removed, the newly created subtree(which is the new leaf itself) and the subtrees that contain its ancestors should be updated. The number of subtrees to be updated is the same as the height of the tree. To update the subtrees, you need to update each ancestor’s size value bottom up. To update one subtree takes a constant time because its children have correct information either because they were unaffected by the change or they already have been updated before we’ve moved on to the subtree at focus. Thus, the whole operation as a whole takes O(height).

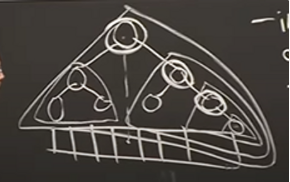
AVL Tree

When the height equals log n, the tree is considered balanced. To rebalance an unbalanced tree, you need the rotation trick. Rebalancing means reorganize the tree without modifying its original traversing order.

An AVL tree is a tree that maintains height balance, so that height(node.right) - height(node.left), or skew(node) is always either -1, 0 or 1. Suppose we have a tree whose node.left is shorter than node.right by 1 in terms of height. The number of nodes in an AVL tree of height H($N_h$) is $N_{h-1}$ + $N_{h-2}$ + 1(root).

💡 $N_h$ > $N_{h-2}$ + $N_{h-2}$ = 2 x $N_{h-2}$
This(2 x $N_{h-2}$) is powers of two thus this is exponential. This implies the height, h, is equal to or smaller than 2 log n.

Height is a subtree property in that node.height = max{node.left.height, node.right.height} + 1. When adding or deleting a node to an AVL tree, the height of a subtree might change, which in turn might make the skew value go out of range of -1, 0 and 1 (the new value is either -2 or 2). To rebalance the tree, you have to rotate it. When skew(y) is either 0 or 1(like in the picture below), you only need to rotate the tree so that y is now the root.

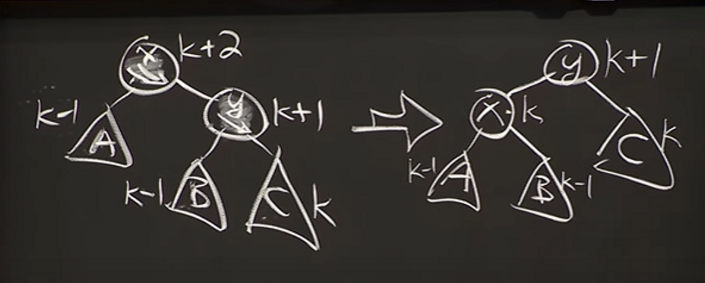
On the contrary, if skew(y) is -1, the rotation gets complicated but still doable.